浙教版备考2022年中考数学二轮复习训练题6：三角形

试卷更新日期：2022-03-16 类型：二轮复习

进入出卷网下载

一、单选题

1. 如图， $△ A B C$ 和 $△ P Q R$ 都是等边三角形，且 $A D = B E = C F = \frac{1}{4} A B$ ，当 $∠ A F R = ∠ B D P = ∠ C E Q = 30 °$ 时， $△ P Q R$ 的面积为 $\sqrt{3}$ ，则 $△ A B C$ 的边长为（）

A、4 B、 $3 \sqrt{3}$ C、 $2 \sqrt{3}$ D、 $\frac{8}{3} \sqrt{3}$

查看试题解析
2. 如图， $O$ 是 $△ A B C$ 的重心，过 $O$ 的一条直线分别与AB、AC相交于G、H（均不与 $△ A B C$ 的顶点重合）， $S_{四边形 B C H G}$ ， $S_{△ A G H}$ 分别表示四边形 $B C H G$ 和 $△ A G H$ 的面积，则 $\frac{S_{四边形 B C H G}}{S_{△ A G H}}$ 的最大值是（）

A、 $\frac{5}{4}$ B、1 C、 $\frac{3}{2}$ D、 $\frac{2}{3}$

查看试题解析
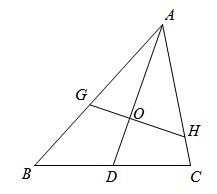3. 在平面直角坐标系中，已知点A（3，﹣3），在坐标轴上确定一点B，使△AOB为等腰三角形，则符合条件的点B共有（）个

A、5 B、6 C、7 D、8

查看试题解析
4. 如图，在平面直角坐标系中，有一个 $R t △ A O B$ ，∠ABO＝90°，∠AOB＝30°，直角边OB在y轴正半轴上，点A在第一象限，且OA＝1，将 $R t △ A O B$ 绕原点逆时针旋转30°，同时把各边长扩大为原来的两倍（即OA₁＝2OA）．得到 $R t △ O A_{1} B_{1}$ ，同理，将 $R t △ O A_{1} B_{1}$ 绕原点O逆时针旋转30°，同时把各边长扩大为原来的两倍，得到 $R t △ O A_{2} B_{2}$ ，…，依此规律，得到 $R t △ O A_{2021} B_{2021}$ ，则 $O B_{2021}$ 的长度为（）

A、 $\frac{\sqrt{3}}{2}$ B、 $\sqrt{3}$ ×2²⁰²⁰ C、 $\sqrt{3}$ ×2²⁰²¹ D、 $\sqrt{3}$ ×2²⁰¹⁹

查看试题解析
5. 如图，在Rt△ABC中，∠ABC=90°，AB=BC，点P在△ABC内一点，连接PA，PB，PC，若∠BAP=∠CBP，且AP = 6，则PC的最小值是（）

A、 $2 \sqrt{2}$ B、 $3$ C、 $3 \sqrt{5} - 3$ D、 $3 \sqrt{2}$

查看试题解析
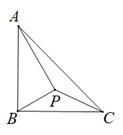6. 如图，已知直线l₁∥l₂ ， l₁、l₂之间的距离AE为 $\sqrt{3}$ ，在△ABC中，BC＝2，AB＝ $\sqrt{7}$ ，将△ABC绕点C在平面内顺时针旋转得到△A′B′C，若旋转角为60°，A′C交直线l₂于点D，则CD的长度为（）

A、 $\frac{\sqrt{57}}{2}$ B、 $\frac{2 \sqrt{19}}{3}$ C、 $\frac{2 \sqrt{19}}{5}$ D、 $\sqrt{19}$ ﹣ $\sqrt{3}$

查看试题解析
7. 如图，在Rt△ABC中， $A B = C B$ ， $B E ⊥ A C$ ，把 $△ A B C$ 折叠，使 $A B$ 落在 $A C$ 上，点 $B$ 与 $A C$ 上的点 $F$ 重合，展开后，折痕 $A D$ 交 $B E$ 于点 $G$ ，连接 $G F$ 、 $B F$ ， $B F$ 交 $A D$ 于 $O$ 点.下列结论：① $\tan ∠ A D B = 2$ ②若将 $△ D G F$ 沿 $G F$ 折叠，则点 $D$ 一定落在 $A C$ 上③图中有7个等腰三角形④若 $S_{△ B D O} = 1$ ，则 $S_{△ A B C} = 6 \sqrt{2} + 8$ ⑤ $S_{四边形 G D F E} = S_{△ A E G}$ ，上述结论中正确的个数是（）

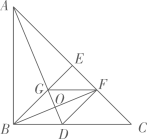A、2个 B、3个 C、4个 D、5个

查看试题解析
8. 著名画家达·芬奇用三个正方形和三个全等的直角三角形拼成如下图形证明了勾股定理，其中 $∠ A C B = ∠ E J D = 90^{°} ， C B = E J$ ，连结HF，CJ，得到4个全等的四边形HFGI，四边形HFBA，四边形CJEA，四边形JCBD.CJ分别交AB，ED于点M，N，若 $M N ： C J = 5 ： 9$ ，且 $A B = 5$ ，则HF的长为（）

A、 $6 \sqrt{3}$ B、 $7 \sqrt{2}$ C、 $8 \sqrt{2}$ D、 $3 \sqrt{10}$

查看试题解析
9. 如图，在▱ABCD中，∠B＝60°，AB＝BC ， AE⊥BC于点E ，连接DE ，交AC于点G ．以DE为边作等边△DEF ，连接AF ，交DE于点N ，交DC于点M ，且M为AF的中点．在下列说法中：①∠EAN＝45°，② $\frac{1}{2}$ AE＝ $\sqrt{3}$ CM ， ③S_△AGE＝S_△DGC ， ④AF⊥DE ．正确的个数有（　　）

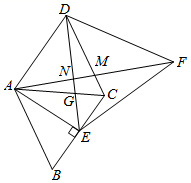A、1个 B、2个 C、3个 D、4个

查看试题解析
10. 如图，△ABC中，AB=AC= $2 \sqrt{5}$ ，∠BAC=α°， $\tan ∠ A B C = \frac{1}{2}$ ，G为BC中点，D为平面内一个动点，且 $D G = \frac{\sqrt{5}}{5}$ .将线段BD绕点D逆时针旋转α°，得到DB′，则四边形BACB′面积的最大值为（）

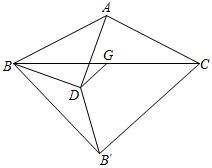A、24 B、25 C、12 D、13

查看试题解析

二、填空题

11. 如图，在△ABC中，4AB=5AC，AD为△ABC的角平分线，点E在BC的延长线上，EF⊥AD于点F，点G在AF上，FG=FD，连接EG交AC于点H.若点H是AC的中点，则 $\frac{A G}{F D}$ 的值为 .

查看试题解析
12. 在菱形 $A B C D$ 中， $A C = 4$ ， $B D = 4 \sqrt{3}$ ， $A C$ ， $B D$ 相交于点 $O$ ．将一个足够大的直角三角板60°角的顶点放在菱形 $A B C D$ 的顶点 $A$ 处，绕点 $A$ 左右旋转，其中三角板60°角的两边分别与边 $B C$ ， $C D$ 相交于点 $E$ ， $F$ ，连接 $E F$ 与 $A C$ 相交于点 $G$ ．旋转过程中，当点 $E$ 为边 $B C$ 的四等分点时（ $B E > C E$ ）， $C G =$ ．

查看试题解析
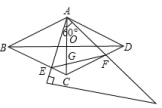13. 如图，在平面直角坐标系中，O为坐标原点，点A、C分别在x轴、y轴的正半轴上，点C（0，2），点Q在x轴的负半轴上，且S_△_CQA＝12，分别以AC、CQ为腰，点C为直角顶点在第一、第二象限作等腰Rt△CAN、等腰Rt△QCM，连接MN交y轴于P点，则OP的值为．

查看试题解析
14. 小华用一张直角三角形纸片玩折纸游戏，如图1，在 $R t △ A B C$ 中， $∠ A C B = 90 °$ ， $∠ B = 30 °$ ， $A C = 1$ ．第一步，在 $A B$ 边上找一点 $D$ ，将纸片沿 $C D$ 折叠，点 $A$ 落在 $A$ 处，如图2，第二步，将纸片沿 $C A$ 折叠，点 $D$ 落在 $D$ 处，如图3．当点 $D$ 恰好在原直角三角形纸片的边上时，线段 $A D$ 的长为．

查看试题解析
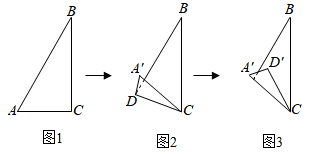15. 在等腰三角形ABC中， $∠ B A C = 120 °$ ， $A B = A C = 8$ ，E为BC上一点， $B E ： B C = 1 ： 4$ ， $D E ∥ A B$ ，交BC于点E，点F为直线DE上一点，则 $F A + F B$ 的最小值为.

查看试题解析
16. 如图，在△ABC中，AD和BE是高，∠ABE=45°，点F是AB的中点，AD与FE、BE分别交于点G、H，∠CBE=∠BAD.有下列结论：①FD=FE；②AH=2CD；③BC•AD= $\sqrt{2}$ AE²；④S△_ABC=4S△_ADF.其中正确的有.

查看试题解析

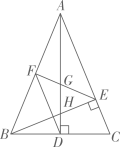
三、综合题

17. 如图所示， $△ A B C$ 中， $B A = B C$ ， $C O ⊥ A B$ 于点 $O$ ， $A O = 4$ ， $B O = 6$ ．

(1)、求 $B C$ ， $A C$ 的长．

(2)、若点 $D$ 是射线 $O B$ 上的一个动点，作 $D E ⊥ A C$ 于点 $E$ ，连结 $O E$ ．
①当点 $D$ 在线段 $O B$ 上时，若 $△ A O E$ 是以 $A O$ 为腰的等腰三角形，请求出所有符合条件的 $O D$ 的长．

②设 $D E$ 交直线 $B C$ 于点 $F$ ，连结 $O F$ ， $C D$ ，若 $S_{△ O B F} ： S_{△ O C F} = 1 ： 4$ ，则 $C D$ 的长为多少？（直接写出结果）．

查看试题解析
18. 如图，在等腰 $R t △ A B C$ 中， $∠ A B C = 90 °$ ，点 $A$ 、 $B$ 分别在 $x$ 轴、 $y$ 轴上.

(1)、如图①，若点 $C$ 的横坐标为5，求点 $B$ 的坐标；

(2)、如图②，若 $x$ 轴恰好平分 $∠ B A C$ ， $B C$ 交 $x$ 轴于点 $M$ ，过点 $C$ 作 $C D ⊥ x$ 轴于点 $D$ ，求 $\frac{C D}{A M}$ 的值；

(3)、如图③，若点 $A$ 的坐标为 $(- 4 ， 0)$ ，点 $B$ 在 $y$ 轴的正半轴上运动时，分别以 $O B$ 、 $A B$ 为边在第一、第二象限中作等腰 $R t △ O B F$ ，等腰 $R t △ A B E$ ，连接 $E F$ 交 $y$ 轴于点 $P$ ，当点 $B$ 在 $y$ 轴上移动时， $P B$ 的长度是否发生改变？若不变求 $P B$ 的值；若变化，求 $P B$ 的取值范围.

查看试题解析
19. 如图，在Rt△ABC中，∠ACB＝90°，AC＝6，∠ABC＝30°，点D，E分别在边AB，AC上，在线段ED左侧构造Rt△DEF，使△DEF∽△BCA .

(1)、如图1，若AD＝BD，点E与点C重合，DF与BC相交于点H.求证：2CH＝BH.

(2)、当AE＝2时，连接BF，取BF的中点G，连接DG.
①如图2，若点F落在AC边上，求DG的长.
②是否存在点D，使得△DFG是直角三角形？若存在，求AD的长；若不存在，试说明理由.

查看试题解析
20. 如图

(1)、（操作发现）如图（1），在△OAB和△OCD中，OA＝OB，OC＝OD，∠AOB＝∠COD＝45°，连接AC，BD交于点M.
①AC与BD之间的数量关系为；

②∠AMB的度数为；

(2)、（类比探究）如图（2），在△OAB和△OCD中，∠AOB＝∠COD＝90°，∠OAB＝∠OCD＝30°，连接AC，交BD的延长线于点M.请计算 $\frac{A C}{B D}$ 的值及∠AMB的度数；

(3)、（实际应用）如图（3），是一个由两个都含有30°角的大小不同的直角三角板ABC、DCE组成的图形，其中∠ACB＝∠DCE＝90°，∠A＝∠D＝30°且D、E、B在同一直线上，CE＝1，BC＝ $\sqrt{21}$ ，求点A、D之间的距离.

查看试题解析
21. 在△ABC中，AB＝AC，∠BAC＝90°，D为平面内的一点.

(1)、如图1，当点D在边BC上时，且∠BAD＝30°，求证：AD= $\sqrt{2}$ BD.

(2)、如图2，当点D在△ABC的外部，且满足∠BDC−∠ADC＝45°，求证：BD= $\sqrt{2}$ AD.

(3)、如图3，若AB＝4，当D、E分别为AB、AC的中点，把△DAE绕A点顺时针旋转，设旋转角为α(0<α≤180∘)，直线BD与CE的交点为P，连接PA，直接写出△PAC面积的最大值.

查看试题解析
22. 在△ABC中，BD⊥AC于点D，点P为射线BD上任一点（点B除外），连接AP，将线段PA绕点P顺时针方向旋转α，α＝∠ABC，得到PE，连接CE.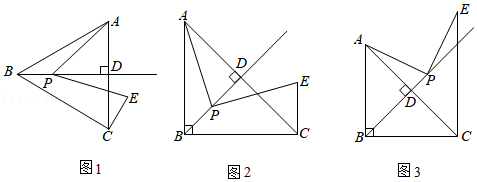

(1)、【观察发现】如图1，当BA＝BC，且∠ABC＝60°时，BP与CE的数量关系是， BC与CE的位置关系是 .

(2)、【猜想证明】如图2，当BA＝BC，且∠ABC＝90°时，（1）中的结论是否成立？若成立，请予以证明；若不成立，请说明理由.（请选择图2，图3中的一种情况予以证明或说理）

(3)、【拓展探究】在（2）的条件下，若AB＝8，AP＝5 $\sqrt{2}$ ，请直接写出CE的长.

查看试题解析
23. 如图，在 $Rt △ A B C$ 中， $∠ C = 90^{\circ} ， A B = 10 ， B C = 6$ ，点 $P$ 以每秒2个单位长度的速度从点 $A$ 出发，沿 $A B$ 方向向终点 $B$ 匀速运动，同时点Q以每秒1个単位长度的速度从点 $C$ 出发，沿 $C A$ 方向向终点 $A$ 匀速运动，连结 $P Q$ . 设运动的时间为 $t$ 秒.

(1)、求 $A Q$ 的长（用含 $t$ 的代数式表示）.

(2)、当 $t = 3$ 秒时，求 $△ A P Q$ 的面积.

(3)、①如图 2，连结 $B Q$ ，当 $△ B P Q$ 为直角三角形时，求所有满足条件 $t$ 的值.
② 如图3，当点 $P$ 关于 $A C$ 的对称点 $P^{'}$ 落在直线 $B Q$ 上时，求 $\frac{P Q}{B Q}$ 的值.

查看试题解析
24. 我们定义：如果一个三角形一条边上的高等于这条边，那么这个三角形叫做“等高底”三角形，这条边叫做这个三角形的“等底”.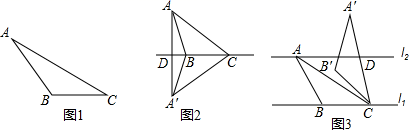

(1)、概念理解：
如图1，在△ABC中，AC＝6，DC＝3，∠ACB＝30°，试判断△ABC是否是“等高底”三角形.（填“是”或“否”）

(2)、问题探究：
如图2，△ABC是“等高底”三角形，BC是“等底”，作△ABC关于BC所在直线的对称图形得到△A'BC，连接AA'交直线BC于点D.若点B是△AA′C的重心，求 $\frac{A C}{B C}$ 的值.

(3)、应用拓展：
如图3，已知l₁∥l₂ ， l₁与l₂之间的距离为2，“等高底”△ABC的“等底”BC在直线l₁上，点A在直线l₂上，有一边的长是BC的 $\sqrt{2}$ 倍.将△ABC绕点C按顺时针方向旋转45°得到△A'B′C，A′C所在直线交l₂于点D，直接写出CD的值.

查看试题解析