重庆市永川区2020-2021学年九年级下学期期中质量检测数学试卷（一诊）

试卷更新日期：2022-03-16 类型：期中考试

进入出卷网下载

一、单选题

1. 在下列四个实数中，是无理数的是（）

A、－2 B、 $\sqrt{2}$ C、－1 D、0

查看试题解析
2. 下面四个图形分别是节能、节水、低碳和绿色食品标志，在这四个标志中，是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. 下列计算正确的是（）

A、 $2 a + 3 b = 5 a b$ B、 $x^{2} \cdot x^{3} = x^{6}$ C、 $6 x y^{2} \div (- 2 x y) = - 3 y$ D、 ${(- 2 x y^{2})}^{3} = - 6 x^{3} y^{6}$

查看试题解析
4. 从重庆市旅游局获悉，据初步统计测算，2020年“国庆·中秋”八天小长假，重庆共接待游客约31 200 000人次，将31 200 000用科学记数法表示为（）

A、 $312 \times 10^{5}$ B、 $31.2 \times 10^{6}$ C、 $3.12 \times 10^{7}$ D、 $0.312 \times 10^{8}$

查看试题解析
5. 如图，△ABC内接于⊙O，连接OB、OC，若∠BAC=64°，则∠OCB的度数为（）

A、64° B、36° C、32° D、26°

查看试题解析
6. 如图，是用△按一定的方式摆成的图案，已知图1需要2个△，图2需要6个△，图3需要11个△，按照这样的方式摆下去，则图6需要（）个△.

A、26 B、28 C、30 D、32

查看试题解析
7. 某工厂现在平均每天比原计划多生产 $50$ 台机器，现在生产 $600$ 台机器所需要时间与原计划生产 $450$ 台机器所需时间相同，现在平均每天生产__________台机器.设现在每天生产 $x$ 台，则方程可为（）.

A、 $\frac{450}{x} = \frac{600}{x + 50}$ B、 $\frac{450}{x + 50} = \frac{600}{x}$ C、 $\frac{450}{x} = \frac{600}{x - 50}$ D、 $\frac{450}{x - 50} = \frac{600}{x}$

查看试题解析
8. 如图，在平面直角坐标系中，每个小方格的边长均为1.△AOB与△ $A^{'} O B^{'}$ 是以原点O为位似中心的位似图形，且相似比为3：2，点A，B都在格点上，则点B′的坐标是（）

A、（－2，1） B、（－2， $\frac{4}{3}$ ） C、（－2， $\frac{5}{4}$ ） D、（－2， $\frac{7}{6}$ ）

查看试题解析
9. 鹅岭公园是重庆最早的私家园林，前身为礼园，是国家级AAA旅游景区，园内有一瞰胜楼，登上高楼能欣赏到重庆的优美景色.周末，李明同学游览鹅岭公园，如图，在点A观察到瞰胜楼楼底点C的仰角为12°，楼顶点D的仰角为13°，测得斜坡BC的坡面距离BC $=$ 510米，斜坡BC的坡度 $i = 8 ： 15$ .则瞰胜楼的高度CD是（）米.（参考数据：tan12°≈0.2，tan13°≈0.23）

A、30 B、32 C、34 D、36

查看试题解析
10. 若关于 $x$ 的一元一次不等式组 ${\begin{array}{l} x - \frac{1}{4} (4 a - 2) \leq \frac{1}{2} \\ \frac{3 x - 1}{2} - 2 < x \end{array}$ 的解集是 $x$ $\leq$ $a$ ，且使关于 $y$ 的分式方程 $\frac{a - 3}{y - 1} = 2 + \frac{2}{1 - y}$ 有非负整数解，则符合条件的所有整数 $a$ 的和为（）

A、2 B、3 C、8 D、9

查看试题解析
11. 在矩形ABCD中，AB＝3，BC＝2 $\sqrt{10}$ ，点E在BC边上，连接DE，将△DEC沿DE翻折，得到△DEC'，C'E交AD于点F，连接AC'.若点F为AD的中点，则AC′的长度为（）

A、 $\sqrt{13}$ B、2 $\sqrt{2}$ C、2 $\sqrt{3}$ D、 $\sqrt{10}$ +1

查看试题解析
12. 如图，反比例函数 $y = \frac{k}{x}$ （ $x$ ＞0）的图象经过矩形OABC对角线的交点M，分别与AB、BC交于点D、E，若四边形ODBE的面积为18，则k的值为（）

A、2 B、4 C、6 D、8

查看试题解析

二、填空题

13. 计算：(-1)²⁰²¹+（4- $π$ ）⁰=.

查看试题解析
14. 如果某个正n边形的每一个外角都等于其相邻内角的 $\frac{1}{2}$ ，则n=.

查看试题解析
15. 现将背面完全相同，正面分别标有数﹣2，﹣1，0，1，2的5张卡片洗匀后，背面朝上，从中任取一张，将该卡片上的数作为点P的横坐标，将该数的相反数作为点P的纵坐标，则点P落在直线 $y = x$ 上方的概率为.

查看试题解析
16. 如图，AB是⊙O的切线，B为切点，AC经过点O，与⊙O分别相交于点D，C，若∠ACB=30°，AB= $\sqrt{3}$ ，则阴影部分的面积是．

查看试题解析
17. 2020年新年，武汉爆发的新型冠状病毒感染的肺炎疫情牵动着全国人民的心，一方有难，八方支援，各地纷纷驰援武汉.某地组织的蔬菜驰援车队从甲地出发匀行驶前往武汉，一段时间后，在甲地的驰援领导小组发现车队漏带有机蔬菜检测证书，于是驰援领导小组立即派一辆轿车匀速前去追赶车队，轿车追上车队后以原速原路返回甲地.车队拿到检测证书后以原速度的 $\frac{4}{3}$ 倍快速赶往武汉，并在从甲地出发后15小时到达武汉（车队被轿车追上交流时间忽略不计）轿车与车队之间相距的路程 $y$ （米）与车队从甲地出发到武汉的行驶时间 $x$ （小时）之间的函数关系如图所示，则轿车返回到甲地时，车队距离武汉的路程为千米.

查看试题解析
18. 假设渝北某商场地下停车场有5个出入口，每天早晨7点开始对外停车且此时车位空置率为75%，在每个出入口的车辆数均是匀速出入的情况下，如果开放2个进口和3个出口，8小时车库恰好停满；如果开放3个进口和2个出口，2小时车库恰好停满，2021年五一节期间，由于商场人数增多，早晨7点时的车位空置率变为60%，又因为车库改造，只能开放2个进口和1个出口，则从早晨7点开始经过小时车库恰好停满.

查看试题解析

三、解答题

19. 计算：

(1)、 ${(a - b)}^{2} - a (a - 2 b)$ ；

(2)、 $(\frac{x - 3}{x - 2} - x - 1) \div \frac{x^{2} - 1}{x - 2}$ .

查看试题解析
20. 如图，在 $▱ A B C D$ 中， $D E = C E$ ，连接 $A E$ 并延长交 $B C$ 的延长线于点 $F$ .

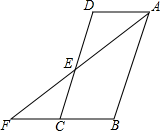(1)、求证：△ADE≌△FCE；

(2)、若AB＝2BC，∠F＝36°.求∠B的度数.

查看试题解析

21. 距离中考体考时间越来越近，永川某中学想了解初三年级学生“清明节”期间在家体育锻炼情况（建议每天30分钟），在初三年级抽取了20名男生和20名女生，对他们“清明节”期间在家锻炼的总时间进行了调查，并收集得到了如下数据：（单位：分钟）

男生	88	60	44	91	71	88	97	63	72	91
男生	81	92	85	85	95	81	91	89	77	86
女生	77	82	85	88	76	87	69	93	66	84
女生	99	88	67	88	91	96	68	97	59	88

（整理数据）按如下分段整理样本数据：

分数

男女

0≤ $x$ ＜60

60≤ $x$ ＜70

70≤ $x$ ＜80

80≤ $x$ ＜90

90≤ $x$ ≤100

男

女

$a$

$b$

(分析数据)对样本数据进行如下统计：

统计量

男女

平均数

中位数

众数

男

81.35

$c$

女

82.40

$d$

(得出结论)

(1)、根据统计，表格中

a

、

b

、

c

、

d

的值分别是、、、 .

(2)、若永川某中学初三年级的男女学生人数分别为600人和500人，则估计“清明节”期间在家锻炼的总时间在90分钟及以上的学生人数.

(3)、根据数据可以推断出男生还是女生的体育锻炼情况更好，请说明理由.

查看试题解析

22. 如果一个正整数能表示为两个正整数的平方差，那么称这个正整数为“智慧数”，否则称这个正整数为“非智慧数”.例如： $2^{2} - 1^{2} = 3$ ； $3^{2} - 2^{2} =5$ ； $3^{2} - 1^{2} =8$ ； $4^{2} - 3^{2} =7$ ； $4^{2} - 2^{2} =12$ ； $4^{2} - 1^{2} =15$ ；，等等.因此3，5，8，都是“智慧数”；而1，2，4，都是“非智慧数”.对于“智慧数”，有如下结论：
①设 $k$ 为正整数（ $k \geq 2$ ），则 $k^{2} - {(k - 1)}^{2} = 2 k - 1$ .∴除1以外，所有的奇数都是“智慧数”；

②设 $k$ 为正整数（ $k \geq 3$ ），则 $k^{2} - {(k - 2)}^{2}$ = ▲ .∴ ▲ 都是“智慧数”.

(1)、补全结论②中的空缺部分；并求出所有大于5而小于20的“非智慧数”；

(2)、求出从1开始的正整数中从小到大排列的第103个“智慧数”.

查看试题解析

23. 探究函数性质时，我们经历了列表、描点、连线，画出函数图象，观察分析图象特征，概括函数性质的过程.结合已有的学习经验，请探究下面函数的性质.

已知函数 $y = \frac{y_{2}}{y_{1}}$ ，其中 $y_{1}$ 与 $x$ 成反比例， $y_{2} = x^{2} + 6 x$ ，且当 $x$ =2时， $y$ =4.

(1)、

y

关于

x

的函数解析式为.

(2)、列表，写出表中

a

，

b

的值：

a

= ▲ ，

b

= ▲ .

描点、连线，在所给的平面直角坐标系中画出该函数的图象.

$x$		-6	-5	-4	-3	-2	-1	0	1	2
$y$		0	$a$	4	$\frac{27}{8}$	2	$\frac{5}{8}$	0	$\frac{7}{8}$	$b$

(3)、已知函数

y =- \frac{1}{3} x + 2

的图象如图所示，结合你所画的函数图象，直接求出方程

\frac{1}{8} x^{3} + \frac{3}{4} x^{2}

- \frac{1}{3} x + 2

的近似解(结果保留一位小数).

查看试题解析

24. “端午节”是我国传统节日，赛龙舟吃粽子，某蛋糕店销售“杏花楼”和“元祖”两个品牌的粽子，每个“杏花楼”粽子的售价是10元，每个“元祖”粽子的售价是8元.

(1)、4月份，两个品牌的粽子一共销售180个，且总销售额不低于1640元，则卖出“杏花楼”粽子至少多少个？

(2)、5月份，粽子大量上市，受此影响，“杏花楼”粽子售价降低了 $a %$ （ $a % < 30 %$ ），销售量在4月份的最低销售量的基础上增加了 $5 a %$ ，“元祖”粽子的售价降低了 $\frac{5}{4} a %$ ，销售量在4月份的最高销售量的基础上增加了 $\frac{5}{2} a %$ ，结果5月份的总销售额比4月份最低销售额增加了680元，求 $a$ 的值.

查看试题解析
25. 如图1，在平面直角坐标系中，直线 $y = x + 4$ 与 $x$ 轴、 $y$ 轴分别交于A、B两点，抛物线 $y = - x^{2} + b x + c$ 经过A、B两点，并且与 $x$ 轴交于另一点C（点C在点A的右侧），点P是抛物线上一动点.

(1)、求抛物线的解析式；

(2)、若点P是第二象限内抛物线上的一个动点，过点P作PD $∥$ $y$ 轴交AB于点D，点E 为线段DB上一点，且DE= $2 \sqrt{2}$ ，过点E作EF $∥$ PD交抛物线于点F，当点P运动到什么位置时，四边形PDEF的面积最大?并求出此时点P的坐标；

(3)、如图2，点F为AO的中点，连接BF，点G为 $y$ 轴负半轴上一点，且GO=2，沿 $x$ 轴向右平移直线AG，记平移过程的直线为 $A^{'} G^{'}$ ，直线 $A^{'} G^{'}$ 交 $x$ 轴于点M，交直线AB于点N.是否存在点M，使得△FMN为等腰三角形，若存在，直接写出平移后点M的坐标；若不存在，请说明理由.

查看试题解析
26. 边长为6的等边△ABC 中，点D ，E 分别在AC ，BC 边上，DE∥AB，EC ＝2 $\sqrt{3}$

(1)、如图1，将△DEC 沿射线EC 方向平移，得到△D′E′C′，边D′E′与AC 的交点为M ，边C′D′与∠ACC′的角平分线交于点N.当CC′多大时，四边形MCND′为菱形？并说明理由.

(2)、如图2，将△DEC 绕点C 旋转∠α(0°<α<360°)，得到△D ′E′C，连接AD′，BE′.边D′E′的中点为P.
①在旋转过程中，AD′和BE′有怎样的数量关系？并说明理由；

②连接AP ，当AP 最大时，求AD′的值.(结果保留根号)

查看试题解析