2021-2022苏科版数学七年级下册9.4乘法公式综合同步练习
试卷更新日期:2022-03-16 类型:同步测试
一、单选题
-
1. 下列运算正确的是( )A、 B、 C、 D、(x+2)(x-2)=x2-42. 如图,大正方形的边长为m,小正方形的边长为n,若用x,y表示四个长方形的两边长(x>y),观察图案及以下关系式:① ;② ;③ ;④ .其中正确的关系式有( )
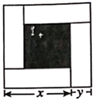 A、①② B、①③ C、①③④ D、①②③④3. 若 ,则 等于( )A、 B、 C、 D、4. 若x2+(k+2)x+9是完全平方式,则k的值为( )A、4 B、±4 C、-8 D、4或-85. 下列多项式相乘时,可用平方差公式的是( )A、 B、 C、 D、6. 将图甲中阴影部分的小长方形变换到图乙位置,能根据图形的面积关系得到的关系式是( )
A、①② B、①③ C、①③④ D、①②③④3. 若 ,则 等于( )A、 B、 C、 D、4. 若x2+(k+2)x+9是完全平方式,则k的值为( )A、4 B、±4 C、-8 D、4或-85. 下列多项式相乘时,可用平方差公式的是( )A、 B、 C、 D、6. 将图甲中阴影部分的小长方形变换到图乙位置,能根据图形的面积关系得到的关系式是( )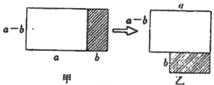 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
7. 若 ,则 =.8. 计算:(-m-n)(m-n)=()9. 若代数式 是一个完全平方式,则 .10. 如图,点M是AB的中点,点P在MB上.分别以AP,PB为边,作正方形APCD和正方形PBEF,连结MD和ME.设AP=a,BP=b,且a+b=10,ab=15.则图中阴影部分的面积为.
 11. 已知 ,化简 = 。12. 如果是一个完全平方式,那么的值为.
11. 已知 ,化简 = 。12. 如果是一个完全平方式,那么的值为.三、计算题
-
13. 计算:(1)、(2)、14. 先化简,再求值:(3x+2)(3x-2)-5x(x+1)-(x-1)2 , 其中x2-x=10.15. 求代数式的值:2(x﹣3)2+(2x+1)(x+1)﹣(x+2)(x﹣2),其中x2﹣3x+1=0.
四、解答题
-
16. 已知 , .求下列各式的值:(1)、 .(2)、 .17. 数学活动课上,张老师准备了若干个如图①的三种纸片,A种纸片是边长为a的正方形,B种纸片是边长为b的正方形,C种纸片是长为b , 宽为a的长方形,并用A种纸片一张,B种纸片一张,C种纸片两张拼成如图②的大正方形.
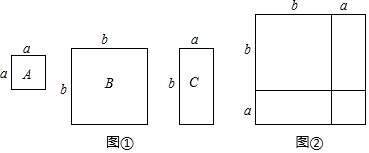 (1)、观察图②,写出代数式(a+b)2 , a2+b2 , ab之间的等量关系是;(2)、根据(1)中的等量关系,解决下列问题;
(1)、观察图②,写出代数式(a+b)2 , a2+b2 , ab之间的等量关系是;(2)、根据(1)中的等量关系,解决下列问题;①已知a+b=4,a2+b2=10,求ab的值;
②已知(x﹣2021)2+(x﹣2019)2=130,直接写出x﹣2020的值.
18. 上数学课时,王老师在讲完乘法公式(a+b)2=a2+2ab+b2的多种运用后,要求同学们运用所学知识解答:求代数式x2+4x+5的最小值?同学们经过交流、讨论,最后总结出如下解答方法;
解:x2+4x+5=x2+4x+4+1=(x+2)2+1, ∵(x+2)2≥0, ∴当x=-2时,(x+2)2的值最小,最小值是0,
∴(x+2)2+1≥1,∴当(x+2) 2=0时,(x+2) 2+1的值最小,最小值是1,∴x2+4x+5的最小值是1。
请你根据上述方法,解答下列各题:
(1)、知识再现:当x=_时, 代数式x2-6x+12的最小值是_;(2)、知识运用:若y=-x2+2x-3,当x=时,y有最_值(填“大”或“小”),这个值是_(3)、知识拓展:若-x2+3x+y+5=0,求y+x的最小值。