2021-2022苏科版数学七年级下册9.4乘法公式2平方差公式（提高）同步练习

试卷更新日期：2022-03-16 类型：同步测试

进入出卷网下载

一、单选题

1. 下列各运算中，正确的是（）

A、（m－2）²＝m²－4 B、（a＋1）（－a－1）＝a²－1 C、（1＋2a）²＝1＋2a＋4a² D、（a＋1）（－1＋a）＝a²－1

查看试题解析
2. 下列多项式相乘，可以用平方差公式直接计算的是（）

A、(x＋5y)(x－5y) B、(－x＋y)(y－x) C、(x＋3y)(2x－3y) D、(3x－2y)(2y－3x)

查看试题解析
3. 下列各式中，与（1﹣a）（﹣a﹣1）相等的是（）

A、a²﹣1 B、a²﹣2a+1 C、a²﹣2a﹣1 D、a²+1

查看试题解析
4. 计算（a+1）（a-1）（a²+1）(a²-1)的结果是（）．

A、a⁸-1 B、a⁸-a⁴+1 C、a⁸-2a⁴+1 D、以上答案都不对

查看试题解析
5. 如图，在边长为 a 的正方形上剪去一个边长为b 的小正方形( a > b )，把剩下的部分剪拼成一个梯形，分别计算这两个图形阴影部分的面积，由此可以验证的等式是（）

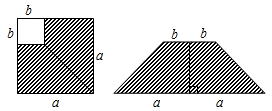A、a² - b² = (a + b)(a - b) B、(a + b)² = a² + 2ab + b² C、(a - b)² = a² - 2ab + b² D、a² - ab = a(a - b)

查看试题解析
6. 记 $x = (1 + 2) (1 + 2^{2}) (1 + 2^{4}) (1 + 2^{8}) \dots (1 + 2^{n})$ ，且 $x + 1 = 2^{128}$ ，则 $n =$ （）．

A、128 B、32 C、64 D、16

查看试题解析

二、填空题

7. 已知 $a + b = \frac{3}{2}$ ， $a b = \frac{1}{2}$ ，并满足 $a > b$ ，则 $a^{2} - b^{2} =$ .

查看试题解析
8. 若x，y互为相反数，则多项式x²﹣y²的值为.

查看试题解析
9. 计算：2019²-2017×2021= ．

查看试题解析
10. （﹣ $\frac{3}{2}$ x﹣11y）（　）= $\frac{9}{4} x^{2}$ ﹣121y² ．

查看试题解析
11.
如图，边长为2m+3的正方形纸片剪出一个边长为m+3的正方形之后，剩余部分可剪拼成一个长方形，若拼成的长方形一边长为m，则另一边长为

查看试题解析
12. 你能化简（x﹣1）（x⁹⁹+x⁹⁸+…+x+1）吗？遇到这样的复杂问题时，我们可以先从简单的情形入手，然后归纳出一些方法，分别化简下列各式并填空：（x﹣1）（x+1）=x²﹣1；（x﹣1）（x²+x+1）=x³﹣1；（x﹣1）（x³+x²+x+1）=x⁴﹣1
…根据上述规律，可得（x﹣1）（x⁹⁹+x⁹⁸+…+x+1）=
请你利用上面的结论，完成下面问题：
计算：2⁹⁹+2⁹⁸+2⁹⁷+…+2+1，并判断末位数字是

查看试题解析

三、解答题

13. 先化简，再求值： $(3 x + 2) (3 x - 2) - 5 x (x + 1) - {(x - 1)}^{2}$ ，其中 $x^{2} - x - 2012 = 0$

查看试题解析
14. 已知a-b=30，b-c=25，且a²-c²=1650，求a+c的值.

查看试题解析
15. 已知： $a^{2} + b^{2} = 5$ ， ${(3 a - 2 b)}^{2} - {(3 a + 2 b)}^{2} = - 48$ ，求 $a + b$ 的值．

查看试题解析

四、综合题

16. 你能化简（x﹣1）（x⁹⁹+x⁹⁸+x⁹⁷+…+x+1）吗？遇到这样的问题，我们可以先思考一下，从简单的情形入手，然后归纳出一些方法．

(1)、分别化简下列各式：
①（x﹣1）（x+1）=；
②（x﹣1）（x²+x+1）=；
③（x﹣1）（x³+x²+1）=；
…
由此我们可以得到：（x﹣1）（x⁹⁹+x⁹⁸+x⁹⁷+…+x+1）= ．

(2)、请你利用上面的结论计算：2⁹⁹+2⁹⁸+2⁹⁷+…+2+1．

查看试题解析
17. 如果一个正整数能表示为两个连续偶数的平方差，那么称这个正整数为“奇巧数”，如 $12 = 4^{2} - 2^{2}$ ， $20 = 6^{2} - 4^{2} ， 28 = 8^{2} - 6^{2}$ ···，因此 $12 ， 20 ， 28$ 都是奇巧数.

(1)、 $36 ， 50$ 是奇巧数吗？为什么？

(2)、奇巧数是 $4$ 的倍数吗？为什么？

查看试题解析
18. 如图①是由边长为a的大正方形纸片剪去一个边长为b的小正方形后余下的图形.我们把纸片剪开后，拼成一个长方形（如图②）.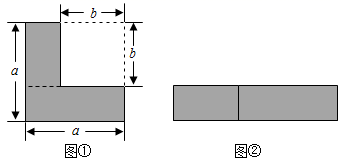

(1)、探究：上述操作能验证的等式的序号是.
① a²＋ab＝a（a+b） ② a²－2ab＋b²＝（a－b）²③ a²－b²＝（a＋b）（a－b）

(2)、应用：利用你从（1）中选出的等式，完成下列各题：
①已知4x²－9y²＝12，2x＋3y＝4，求2x－3y的值；

②计算 $(1- \frac{1}{2^{2}}) \times (1- \frac{1}{3^{2}}) \times (1- \frac{1}{4^{2}}) \times (1- \frac{1}{5^{2}}) \times \dots \times (1- \frac{1}{100^{2}})$

查看试题解析