2021-2022苏科版数学七年级下册9.4乘法公式2平方差公式(基础)同步练习
试卷更新日期:2022-03-16 类型:同步测试
一、单选题
-
1. 下列式子中,能用平方差公式运算的是( )A、 B、 C、 D、2. 下列计算中:①x(2x2﹣x+1)=2x3﹣x2+1;②(a+b)2=a2+b2;③(x﹣4)2=x2﹣4x+16;④(5a﹣1)(﹣5a﹣1)=25a2﹣1;⑤(﹣a﹣b)2=a2+2ab+b2 , 错误的个数有( )A、2个 B、3个 C、4个 D、5个3. 下列各式计算正确的是( )A、 B、 C、 D、4. 算式(2+1)×(22+1)×(24+1)×…×(232+1)+1计算结果的个位数字是( )A、8 B、6 C、4 D、25. 分别表示出下图阴影部分的面积,可以验证公式( )

 A、(a+b)2=a2+2ab+b2 B、(a-b)2=a2-2ab+b2 C、a2-b2=(a+b)(a-b) D、(a+2b)(a-b)=a2+ab-2b26. 如图,从边长为 的大正方形纸片中剪去一个边长为 的小正方形 ,剩余部分沿虚线剪开,拼成一个矩形(不重叠无缝隙),则矩形的面积为( )
A、(a+b)2=a2+2ab+b2 B、(a-b)2=a2-2ab+b2 C、a2-b2=(a+b)(a-b) D、(a+2b)(a-b)=a2+ab-2b26. 如图,从边长为 的大正方形纸片中剪去一个边长为 的小正方形 ,剩余部分沿虚线剪开,拼成一个矩形(不重叠无缝隙),则矩形的面积为( )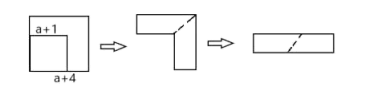 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
7. 计算(a-b)2-(a+b)2的结果是.8. 小丽在计算 时,把 写成 后,发现可以连续运用平方差公式进行计算.用类似方法计算: .9. 若 , ,则代数式a+b的值是.10. ,则 .11. .12. 如图,大正方形的边长为 小正方形的边长为 若用 表示四个小长方形两边长(x>y), 观察图案以下关系式正确的是. (填序号)
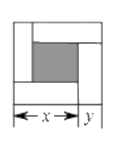
① ;② ③ ;④
三、计算题
-
13. 计算:(1)、 ;(2)、 .14. 先化简,再求值: ,其中
四、综合题
-
15. 从边长为a的正方形中剪掉一个边长为b的正方形(如图1),然后将剩余部分拼成一个长方形(如图2).
 (1)、探究:上述操作能验证的等式是:(请选择正确的一个)
(1)、探究:上述操作能验证的等式是:(请选择正确的一个)A. B. C.
(2)、应用:利用你从(1)选出的等式,完成下列各题:①已知 , ,求 的值;
②计算: .
16. 张老师在黑板上写了三个算式,希望同学们认真观察,发现规律.请你结合这些算式,解答下列问题:请观察以下算式:
①32﹣12=8×1
②52﹣32=8×2
③72﹣52=8×3
(1)、请你再写出另外两个符合上述规律的算式;(2)、验证规律:设两个连续奇数为2n+1,2n﹣1(其中n为正整数),则它们的平方差是8的倍数;(3)、拓展延伸:“两个连续偶数的平方差是8的倍数”,这个结论正确吗?17.(1)、如图1所示,若大正方形的边长为 , 小正方形的边长为 , 则阴影部分的面积是;若将图1中的阴影部分裁剪下来,重新拼成如图2所示的一个长方形,则它的面积是; (2)、由(1)可以得到一个乘法公式是;(3)、利用你得到的公式计算: .
(2)、由(1)可以得到一个乘法公式是;(3)、利用你得到的公式计算: .