河南省南阳市南召县2021-2022学年九年级下学期开学抽考数学试卷
试卷更新日期:2022-03-15 类型:开学考试
一、单选题
-
1. 下列各式是最简二次根式的是( )A、 B、 C、 D、2. 关于x的一元二次方程 有两个不相等的实数根,则a的值可以是( )A、0 B、1 C、-5 D、-23. 如图,圆的两条弦AB,CD相交于点E,且 , ∠A=40°,则∠DEB的度数为( )
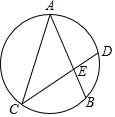 A、50° B、100° C、70° D、80°4. 在平面直角坐标系 中, 的直角顶点B在y轴上,点A的坐标为 ,将 沿直线 翻折,得到 ,过 作 垂直于 交y轴于点C,则点C的坐标为( )
A、50° B、100° C、70° D、80°4. 在平面直角坐标系 中, 的直角顶点B在y轴上,点A的坐标为 ,将 沿直线 翻折,得到 ,过 作 垂直于 交y轴于点C,则点C的坐标为( )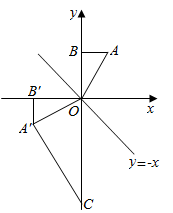 A、 B、 C、 D、5. 下列关于二次函数y=2x2的说法正确的是( )A、它的图象经过点(-1,-2) B、它的图象的对称轴是直线x=2 C、当x<0时,y随x的增大而增大 D、当-12时,y有最大值为8,最小值为06. 下表是小红填写的实践活动报告的部分内容:
A、 B、 C、 D、5. 下列关于二次函数y=2x2的说法正确的是( )A、它的图象经过点(-1,-2) B、它的图象的对称轴是直线x=2 C、当x<0时,y随x的增大而增大 D、当-12时,y有最大值为8,最小值为06. 下表是小红填写的实践活动报告的部分内容:
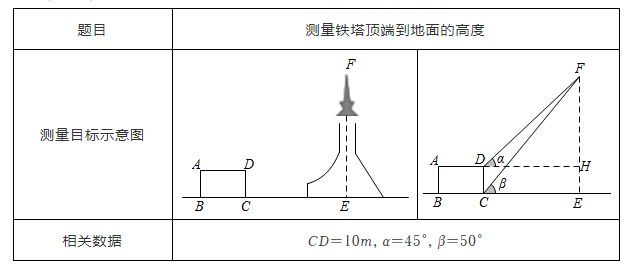
设铁塔顶端到地面的高度 为xm,根据以上条件,可以列出的方程为( )
A、 B、 C、 D、7. 下列语句中:①平分弦的直径垂直于弦;②相等的圆心角所对的弧相等;③长度相等的两条弧是等弧;④圆是轴对称图形,任何一条直径都是它的对称轴;⑤在同圆或等圆中,如果两条弦相等,那么他们所对的圆周角相等,不正确的有( )A、2个 B、3个 C、4个 D、5个8. 看了《田忌赛马》故事后,数学兴趣小组用数学模型来分析:齐王与田忌的上中下三个等级的三匹马综合指标数如表,每匹马只赛一场,综合指标的两数相比,大数为胜,三场两胜则赢,已知齐王的三匹马出场顺序为6、4、2,若田忌的三匹马随机出场,则田忌能赢得比赛的概率为( )马匹等级
下等马
中等马
上等马
齐王
2
4
6
田忌
1
3
5
A、 B、 C、 D、9. 将关于x的一元二次方程 变形为 ,就可以将 表示为关于x的一次多项式,从而达到“降次”的目的,又如 …,我们将这种方法称为“降次法”,通过这种方法可以化简次数较高的代数式.根据“降次法”,已知: ,且 ,则 的值为( )A、 B、 C、 D、10. 如图 和 都是边长为2的等边三角形,它们的边 在同一条直线l上,点C,E重合,现将 沿着直线l向右移动,直至点B与F重合时停止移动.在此过程中,设点移动的距离为x,两个三角形重叠部分的面积为y,则y随x变化的函数图象大致为( ) A、
A、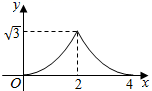 B、
B、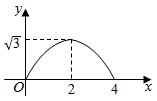 C、
C、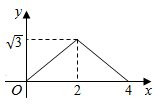 D、
D、
二、填空题
-
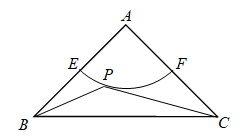
11. 若sinA= ,则锐角∠A=°.12. 二次函数的图象与x轴无交点,写出一个满足条件的实数c的值为.13. 设a、b是方程的两个实数根,则的值为.14. △ABC中,AB=8,AC=6,点D在AC上且AD=2,如果要在AB上找一点E,使△ADE与原三角形相似,那么AE=15. 如图,在△ABC中,∠A=90°,AB=AC=4,点E、F分别是边AB、AC的中点,点P是以A为圆心、以AE为半径的圆弧上的动点,则的最小值为.
三、解答题
-
16.(1)、计算:(2)、用公式法解方程:17. 已知关于x的一元二次方程.(1)、求证:该方程总有两个实数根;(2)、若m>0,且该方程的两个实数根的差为6,求m的值.18. 一只不透明袋子中装有1个白球和若干个红球,这些球除颜色外都相同,某课外学习小组做摸球试验:将球搅匀后从中任意摸出1个球,记下颜色后放回、搅匀,不断重复这个过程,获得数据如下:
摸球的次数
200
300
400
1000
1600
2000
摸到白球的频数
72
90
130
334
532
667
摸到白球的频率
0.3600
0.3100
0.3250
0.3340
0.3325
0.3335
(1)、该学习小组发现,摸到白球的频率在一个常数附近摆动,这个常数是(精确到),由此估出红球有个.(2)、现从该袋中摸出2个球,请用树状图或列表的方法列出所有等可能的结果,并求恰好摸到1个白球,1个红球的概率.19. 如图,⊙O的半径为4,点E在⊙O上,OE⊥弦AB,垂足为D,.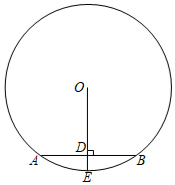 (1)、求AB的长;(2)、若点C为⊙O上的一点(不与A,B重合),直接写出∠ACB的度数.20. 如图,在某小区内拐角处的一段道路上,有一儿童在C处玩耍,一辆汽车从被楼房遮挡的拐角另一侧的A处驶来,已知CM=3m,CO=5m,DO=3m,∠AOD=70°,汽车从A处前行多少米才能发现C处的儿童(结果保留整数)?(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75;sin70°≈0.94,cos70°≈0.34,tan70°≈2.75)
(1)、求AB的长;(2)、若点C为⊙O上的一点(不与A,B重合),直接写出∠ACB的度数.20. 如图,在某小区内拐角处的一段道路上,有一儿童在C处玩耍,一辆汽车从被楼房遮挡的拐角另一侧的A处驶来,已知CM=3m,CO=5m,DO=3m,∠AOD=70°,汽车从A处前行多少米才能发现C处的儿童(结果保留整数)?(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75;sin70°≈0.94,cos70°≈0.34,tan70°≈2.75)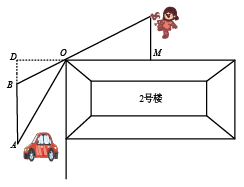 21. 某超市经销一种商品,每千克成本为50元,经试销发现,该种商品的每天销售量y(千克)与销售单价x(元/千克)满足一次函数关系,其每天销售单价,销售量的四组对应值如下表所示:
21. 某超市经销一种商品,每千克成本为50元,经试销发现,该种商品的每天销售量y(千克)与销售单价x(元/千克)满足一次函数关系,其每天销售单价,销售量的四组对应值如下表所示:销售单价x(元/千克)
55
60
65
70
销售量y(千克)
70
60
50
40
(1)、求y(千克)与x(元/千克)之间的函数表达式;(2)、为保证某天获得600元的销售利润,则该天的销售单价应定为多少?(3)、当销售单价定为多少时,才能使当天的销售利润最大?最大利润是多少?22. 如图,已知抛物线y=ax2+bx+6经过两点A(﹣1,0),B(3,0),C是抛物线与y轴的交点.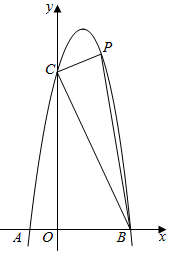 (1)、求抛物线的解析式;(2)、点P(m,n)在平面直角坐标系第一象限内的抛物线上运动,设△PBC的面积为S,求S关于m的函数表达式(指出自变量m的取值范围)和S的最大值;(3)、点M在抛物线上运动,点N在y轴上运动,是否存在点M、点N使得∠CMN=90°,且△CMN与△OBC相似,如果存在,请求出点M和点N的坐标.23. 如图1,在四边形ABCD中, , 点E在边BC上,且 , , 作交线段AE于点F,连接BF.
(1)、求抛物线的解析式;(2)、点P(m,n)在平面直角坐标系第一象限内的抛物线上运动,设△PBC的面积为S,求S关于m的函数表达式(指出自变量m的取值范围)和S的最大值;(3)、点M在抛物线上运动,点N在y轴上运动,是否存在点M、点N使得∠CMN=90°,且△CMN与△OBC相似,如果存在,请求出点M和点N的坐标.23. 如图1,在四边形ABCD中, , 点E在边BC上,且 , , 作交线段AE于点F,连接BF. (1)、求证:;(2)、如图2,若 , , , 求BE的长;(3)、如图3,若BF的延长线经过AD的中点M,求的值.
(1)、求证:;(2)、如图2,若 , , , 求BE的长;(3)、如图3,若BF的延长线经过AD的中点M,求的值.