湖南省株洲市2021年中考模拟试卷数学试卷(二)
试卷更新日期:2022-03-15 类型:中考模拟
一、单选题
-
1. 下列各数中,是负数的是( )A、-1 B、0 C、0.2 D、2. 有理数 a 在数轴上的位置如图所示,下列各数中,可能在 1 到 2 之间的是( )
 A、-a B、 C、-1 D、1 -a3. 下列全国各地地铁标志图中,既是轴对称图形又是中心对称图形的是( )
A、-a B、 C、-1 D、1 -a3. 下列全国各地地铁标志图中,既是轴对称图形又是中心对称图形的是( )
A、 B、
B、 C、
C、 D、
D、 4. 一组数据2,3,4,5,5,8的中位数是( )A、4 B、4.5 C、5 D、6.55. 平面直角坐标系中,直线y=2x﹣6不经过( )A、第一象限 B、第二象限 C、第三象限 D、第四象限6. 如图,AB∥CD,EF平分∠AEG,若∠EGF=40°,那么∠EFG的度数为( )
4. 一组数据2,3,4,5,5,8的中位数是( )A、4 B、4.5 C、5 D、6.55. 平面直角坐标系中,直线y=2x﹣6不经过( )A、第一象限 B、第二象限 C、第三象限 D、第四象限6. 如图,AB∥CD,EF平分∠AEG,若∠EGF=40°,那么∠EFG的度数为( ) A、35° B、40° C、70° D、140°7. 如图,正方形ABCD的边长为1,取AB中点E,取BC中点F,连接DE、AF,DE与AF交于点O.连接OC,则OC的值为( )
A、35° B、40° C、70° D、140°7. 如图,正方形ABCD的边长为1,取AB中点E,取BC中点F,连接DE、AF,DE与AF交于点O.连接OC,则OC的值为( )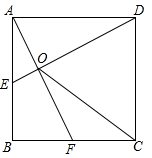 A、 B、1 C、 D、8. 如图,P为边AB上一点且AP::、F分别是的中点,、的面积分别为S和 , 则S和的关系式( )
A、 B、1 C、 D、8. 如图,P为边AB上一点且AP::、F分别是的中点,、的面积分别为S和 , 则S和的关系式( ) A、 B、 C、 D、9. 若点P在某一个函数的图象上,且点P的横纵坐标相等,则称点P为这个函数的“优级点”
A、 B、 C、 D、9. 若点P在某一个函数的图象上,且点P的横纵坐标相等,则称点P为这个函数的“优级点” 若关于的二次函数有两个“优级点”,则的取值范围为( ) A、 B、 C、或 D、或
若关于的二次函数有两个“优级点”,则的取值范围为( ) A、 B、 C、或 D、或二、多选题
-
10. 下列运算正确的是( )A、 B、 C、 D、
三、填空题
-
11. 如图,点O为直线AB上一点, , 则的度数为.
 12. 分解因式: .13. 据科学家估计,地球的年龄大约是4600000000年,这个数用科学记数法表示为.14. 当时,分式的值为0.15. 在-3,-2,1,2,3五个数中随机选取一个数作为二次函数中的值,则该二次函数图象开口向上的概率是.16. 如图,AB是⊙O的直径,BD、CD分别是过⊙O上点B、C的切线,且∠BDC=110°.连接AC,则∠A=°.
12. 分解因式: .13. 据科学家估计,地球的年龄大约是4600000000年,这个数用科学记数法表示为.14. 当时,分式的值为0.15. 在-3,-2,1,2,3五个数中随机选取一个数作为二次函数中的值,则该二次函数图象开口向上的概率是.16. 如图,AB是⊙O的直径,BD、CD分别是过⊙O上点B、C的切线,且∠BDC=110°.连接AC,则∠A=°. 17. 如图,学校环保社成员想测量斜坡CD旁一棵树AB的高度,他们先在点C处测得树顶B的仰角为60°,然后在坡顶D测得树顶B的仰角为30°,已知斜坡CD的长度为20m,DE的长为10m,则树AB的高度是m.
17. 如图,学校环保社成员想测量斜坡CD旁一棵树AB的高度,他们先在点C处测得树顶B的仰角为60°,然后在坡顶D测得树顶B的仰角为30°,已知斜坡CD的长度为20m,DE的长为10m,则树AB的高度是m.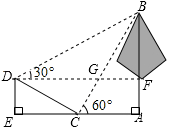 18. 如图,矩形ABCD中,AB=3,BC=4,动点P从B点出发,在BC上移动至点C停止.记 , 点D到直线PA的距离为 , 则关于的函数解析式是.
18. 如图,矩形ABCD中,AB=3,BC=4,动点P从B点出发,在BC上移动至点C停止.记 , 点D到直线PA的距离为 , 则关于的函数解析式是.
四、解答题
-
19. 计算:20. 先化简,再求值: , 其中.21. 如图,、为河对岸的两幢建筑物,某学习小组为了测出河宽(沿岸是平行的),先在岸边的点处测得 , 再沿着河岸前进10米后到达点,在点处测得 , .
 (1)、求河宽;(2)、该小组发现此时还可求得、之间的距离,请求出的长.(精确到0.1米)(参考数据: , , , )22. 某中学开展“我最喜欢的校男篮球员”的调查,要求学生从A、B、C、D、E五名球员中必选且只选一人,现随机抽查了部分学生,如图所示为校篮球社团整理数据后绘制的不完整的统计图表.
(1)、求河宽;(2)、该小组发现此时还可求得、之间的距离,请求出的长.(精确到0.1米)(参考数据: , , , )22. 某中学开展“我最喜欢的校男篮球员”的调查,要求学生从A、B、C、D、E五名球员中必选且只选一人,现随机抽查了部分学生,如图所示为校篮球社团整理数据后绘制的不完整的统计图表.选项 频数 频率 A a 0.20 B 8 0.16 C 14 b D 12 0.24 E 6 0.12 
请根据图中所给出的信息,解答下列各题:
(1)、本次抽样调查的样本容量为;(2)、 , ;(3)、请根据以上信息直接补全频数分布直方图;(4)、若该校共有1500名学生,请你估计全校最喜欢C的学生人数.23. 如图,在四边形ABCD中,AB∥DC,AB=AD,对角线AC,BD交于点O,AC平分∠BAD,过点C作CE⊥AB交AB的延长线于点E,连接OE.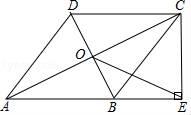 (1)、求证:四边形ABCD是菱形;(2)、若AB= ,BD=2,求OE的长.24. 如图,C,D为⊙O上两点,且在直径AB两侧,连结CD交AB于点E,G是上一点,∠ADC=∠G.
(1)、求证:四边形ABCD是菱形;(2)、若AB= ,BD=2,求OE的长.24. 如图,C,D为⊙O上两点,且在直径AB两侧,连结CD交AB于点E,G是上一点,∠ADC=∠G.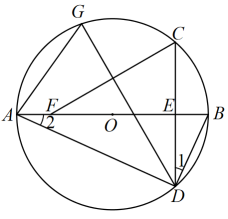 (1)、求证:∠1=∠2;(2)、点C关于DG的对称点为F,连结CF,当点F落在直径AB上时,CF=10,tan∠1= , 求⊙O的半径.25. 如图,矩形OABC中,OC=4,OA=3,分别以OC、OA所在的直线为x轴、y轴,建立如图所示的坐标系,反比例函数y=(x>0)的图象经过点B.
(1)、求证:∠1=∠2;(2)、点C关于DG的对称点为F,连结CF,当点F落在直径AB上时,CF=10,tan∠1= , 求⊙O的半径.25. 如图,矩形OABC中,OC=4,OA=3,分别以OC、OA所在的直线为x轴、y轴,建立如图所示的坐标系,反比例函数y=(x>0)的图象经过点B.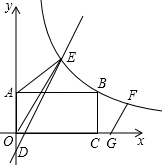 (1)、求反比例函数的解析式;(2)、一次函数y=ax﹣1的图象与y轴交于点D,与反比例函数y=(x>0)的图象交于点E,且△ADE的面积为6,求一次函数的解析式;(3)、将线段OE沿x轴以每秒1个单位长度的速度向右平移,设运动时间为t,平移后的线段与反比例函数y=(x>0)的图象交于点F,与x轴交于点G,t为何值时,GF=OE?26. 如图,抛物线y=mx2-16mx+48m(m>0)与x轴交于A、B两点(点B在点A左侧),与y轴交于点C,点D是抛物线上的一个动点,且位于第四象限,连接OD、BD、AC、AD,延长AD交y轴于点E.
(1)、求反比例函数的解析式;(2)、一次函数y=ax﹣1的图象与y轴交于点D,与反比例函数y=(x>0)的图象交于点E,且△ADE的面积为6,求一次函数的解析式;(3)、将线段OE沿x轴以每秒1个单位长度的速度向右平移,设运动时间为t,平移后的线段与反比例函数y=(x>0)的图象交于点F,与x轴交于点G,t为何值时,GF=OE?26. 如图,抛物线y=mx2-16mx+48m(m>0)与x轴交于A、B两点(点B在点A左侧),与y轴交于点C,点D是抛物线上的一个动点,且位于第四象限,连接OD、BD、AC、AD,延长AD交y轴于点E.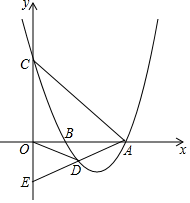 (1)、若△OAC为等腰直角三角形,求m的值.(2)、若对任意m>0,C、E两点总关于原点对称,求点D的坐标(用含m的式子表示).(3)、当点D运动到某一位置时,恰好使得∠ODB=∠OAD,且点D为线段AE的中点,此时对于该抛物线上任意一点P(x0 , y0)总有n≥-4my02-12y0-50成立,求实数n的最小值.
(1)、若△OAC为等腰直角三角形,求m的值.(2)、若对任意m>0,C、E两点总关于原点对称,求点D的坐标(用含m的式子表示).(3)、当点D运动到某一位置时,恰好使得∠ODB=∠OAD,且点D为线段AE的中点,此时对于该抛物线上任意一点P(x0 , y0)总有n≥-4my02-12y0-50成立,求实数n的最小值.
-