湖北省襄阳市2021年中考数学模拟试卷

试卷更新日期：2022-03-15 类型：中考模拟

进入出卷网下载

一、单选题

1. 下列各数中是无理数的是（）

A、 $\sqrt{8}$ B、 $\sqrt[3]{8}$ C、 $π^{0}$ D、 $- \frac{1}{2}$

查看试题解析
2. 在下列四个实数中，最大的数是（）

A、﹣1 B、﹣ $\sqrt{2}$ C、 $\frac{2}{3}$ D、 $\frac{1}{2}$

查看试题解析
3. 如图，在△ABC中，∠B＝55°，∠C＝63°，DE∥AB，则∠DEC等于（）

A、63° B、62° C、55° D、118°

查看试题解析
4. 下列图形中，只有两条对称轴的是（）

A、正六边形 B、矩形 C、等腰梯形 D、圆

查看试题解析
5. 不等式组 ${\begin{array}{l} x \leq 2 \\ x > - 1 \end{array}$ 的解表示在数轴上，正确的是（）

A、 B、 C、 D、

查看试题解析
6. 下列说法正确的是（）

A、平行四边形既是中心对称图形也是轴对称图形 B、矩形的对角线不可能垂直 C、菱形的对角线不可能相等 D、对角线互相平分、垂直且相等的四边形是正方形

查看试题解析
7. 已知一组数据为5，7， $x$ ， 3，4，6，若这组数据的平均数为5，则这组数据的方差为（）

A、 $\frac{3}{2}$ B、 $\frac{5}{3}$ C、 $\frac{11}{6}$ D、10

查看试题解析
8. 我国古代数学名著《孙子算经》记载一道题，大意为100个和尚吃了100个馒头，已知1个大和尚吃3个馒头，3个小和尚吃1个馒头，问有几个大和尚，几个小和尚？若设有 $m$ 个大和尚， $n$ 个小和尚，那么可列方程组为（）

A、 ${\begin{array}{l} m + n = 100 \\ 3 m + 3 n = 100 \end{array}$ B、 ${\begin{array}{l} m + n = 100 \\ m + 3 n = 100 \end{array}$ C、 ${\begin{array}{l} m + n = 100 \\ 3 m + \frac{n}{3} = 100 \end{array}$ D、 ${\begin{array}{l} m + n = 100 \\ 3 m + n = 100 \end{array}$

查看试题解析
9. 如图， $A B$ 是 $⊙ O$ 的弦， $O E ⊥ A B$ ， $E O$ 的延长线交 $⊙ O$ 于点 $F$ ，若 $E F = 8$ ， $s i n A = \frac{3}{5}$ ，则 $A B$ 长为（）

A、3 B、4 C、5 D、8

查看试题解析
10. 二次函数 $y = m x^{2} + m x (m < 0)$ 的图象大致是（）

A、 B、 C、 D、

查看试题解析

二、填空题

11. 数0.0000046用科学记数法表示为：．

查看试题解析
12. 若分式 $\frac{x^{2} - 4}{x - 2}$ 的值为0，则x的值为．

查看试题解析
13. 在一个不透明的口袋中装有4个完全相同的小球，把它们分别标号为1，2，3，4，从中随机摸出两个小球，其标号之和大于4的概率为.

查看试题解析
14. 飞机着陆后滑行的距离s（单位：m）关于滑行的时间t（单位：s）的函数解析式是s＝60t﹣1.5t² ，飞机着陆后滑行米才能停下来.

查看试题解析
15. 如图，在直线l上依次摆放着七个正方形，已知斜放置的三个正方形的面积分别为1.0，1.21，1.44，正放置的四个正方形的面积为S₁、S₂、S₃、S₄ ，则S₁+S₂+S₃+S₄=.

查看试题解析
16. 边长为2 $\sqrt{2}$ 的正方形的对角线长为．

查看试题解析

三、解答题

17. 先化简，再从﹣1、2、3、4中选一个合适的数作为x的值代入求值． $(\frac{x^{2} - 2 x}{x^{2} - 4 x + 4} - \frac{4}{x - 2}) \div \frac{x - 4}{x^{2} - 4}$ .

查看试题解析
18. 如图，在△ABC中，AB=AC，∠BAC=120°，AB边上的垂直平分线与AB、BC交于点D、E，AC边上的垂直平分线与AC、BC分别交于点G、F，

(1)、△AEF是什么形状？你能证明吗？

(2)、连结DG，你能根据学过的相似三角形的知识证明DG= $\frac{1}{2}$ BC吗？

(3)、DG=5cm，试求△AEF的周长.

查看试题解析
19.
为了促进学生多样化发展，某校组织开展了社团活动，分别设置了体育类、艺术类、文学类及其它类社团（要求人人参与社团，每人只能选择一项）．为了解学生喜爱哪种社团活动，学校做了一次抽样调查．根据收集到的数据，绘制成如下两幅不完整的统计图，请根据图中提供的信息，完成下列问题：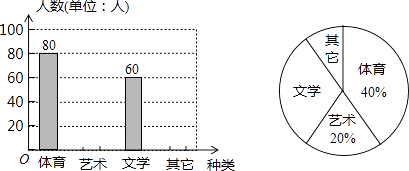

(1)、此次共调查了多少人？

(2)、求文学社团在扇形统计图中所占圆心角的度数；

(3)、请将条形统计图补充完整；

(4)、若该校有1500名学生，请估计喜欢体育类社团的学生有多少人？

查看试题解析
20. 如图所示，某中学九年级数学活动小组选定测量学校前面小河对岸大树 $B C$ 的高度，他们在斜坡上 $D$ 处测得大树顶端 $B$ 的仰角是 $30 °$ ，朝大树方向下坡走6米到达坡底 $A$ 处，在 $A$ 处测得大树顶端 $B$ 的仰角是 $45 °$ ，若斜坡 $F A$ 的坡比 $i = 1$ ： $\sqrt{3}$ ，求大树的高度.（结果保留整数）参考数据：（ $\sqrt{3}$ 取1.7）

查看试题解析

21. 已知关于x函数y＝|﹣x²+bx﹣7|﹣4，点（4，5）在函数上，且b为整数，根据我们已有的研究函数的经验，请对该函数及其图象进行如下探究，并完成以下问题：

(1)、求b＝；

(2)、函数图象探究：

①下表是y与x的几组对应值，请直接写出m与n的值：m＝▲ ， n＝▲；

x	…	﹣ $\frac{1}{4}$	0	$\frac{1}{2}$	1	2	3	4	5	6	7	7 $\frac{1}{2}$	8	8 $\frac{1}{4}$	…
y	…	m	3	$\frac{3}{4}$	﹣4	1	4	n	4	1	﹣4	$\frac{3}{4}$	3	5 $\frac{1}{16}$	…

②根据你喜欢的方式，在如图所示的平面直角坐标系中，画出该函数图象；

(3)、结果函数图象，写出该函数的一条性质：；

(4)、若关于x的方程|﹣x²+bx﹣7|＝m+4有四个根，则m的取值范围为.

查看试题解析

22. 如图，线段 $A B = 4$ ，以线段 $A B$ 为直径画 $⊙ O$ ， $C$ 为 $⊙ O$ 上的动点，连接 $O C$ ，过点 $A$ 作 $⊙ O$ 的切线与 $B C$ 的延长线交于点 $D$ ， $E$ 为 $A D$ 的中点，连接 $C E$ .

(1)、求证： $C E$ 是 $⊙ O$ 的切线；

(2)、点 $C$ 在线段 $B D$ 的哪个位置时，四边形 $A O C E$ 为正方形？请说明理由.

查看试题解析
23. 某销售商计划购进甲、乙两种商品共 $1000$ 件进行销售.已知甲种商品每件进价 $20$ 元，乙种商品每件进价 $80$ 元；通过市场考察，销售商决定甲种商品以每件 $30$ 元的价格出售，乙种商品以每件 $100$ 元的价格出售.设销售商购进的甲种商品有x件，销售完甲、乙两种商品后获得的总利润为y元

(1)、求y与x的函数关系式；

(2)、如果销售商购进的甲种商品的数量不少于乙种商品数量的 $4$ 倍，请求出获利最大的进货方案，所获得的最大利润是多少元？

查看试题解析
24. 在直角坐标系中，已知点 $A$ 、 $B$ 的坐标是 $(a ， 0) (b ， 0)$ ， $a$ ， $b$ 满足方程组 ${\begin{array}{l} 2 a + b = - 5 \\ 3 a - 2 b = - 11 \end{array}$ ， $C$ 为 $y$ 轴正半轴上一点，且 $S_{△ A B C} = 6$ .

(1)、求 $A$ 、 $B$ 、 $C$ 三点的坐标；

(2)、是否存在点 $P (t ， t)$ ，使 $S_{△ P A B} = \frac{1}{3} S_{△ A B C}$ ？若存在，请求出 $P$ 点坐标；若不存在，请说明理由；

(3)、若点 $C$ 沿 $x$ 轴负半轴方向以每秒1个单位长度平移至点 $D$ ，当运动时间 $t$ 为多少秒时，四边形 $A B C D$ 的面积 $S$ 为15个平方单位？求出此时点 $D$ 的坐标.

(4)、连接 $A D$ 、 $C D$ ，若 $P$ 为 $C B$ 上一动点（不与 $C$ 、 $B$ 重合）连接 $D P$ 、 $A P$ ，探究点 $P$ 在运动过程中， $∠ C D P$ 、 $∠ B A P$ 、 $∠ D P A$ 之间的数量关系并证明.

查看试题解析
25. （问题提出）
如图①，在 $△ A B C$ 中，若 $A B = 6$ ， $A C = 4$ ，求 $B C$ 边上的中线 $A D$ 的取值范围.

(1)、【问题解决】
解决此问题可以用如下方法：延长 $A D$ 到点 $E$ 使 $D E = A D$ ，再连接 $B C$ （或将 $△ A C D$ 绕着点 $D$ 逆时针旋转 $180 °$ 得到 $△ E B D$ ），把 $A B$ 、 $A C$ 、 $2 A D$ 集中在 $△ A B E$ 中，利用三角形三边的关系即可判断，由此得出中线 $A D$ 的取值范围.

(2)、【应用】
如图②，在 $△ A B C$ 中， $D$ 为 $B C$ 的中点，已知 $A B = 5$ ， $A C = 3$ ， $A D = 2$ ，求 $B C$ 的长.

(3)、【拓展】
如图③，在 $△ A B C$ 中， $∠ A = 90 °$ ，点 $D$ 是边 $B C$ 的中点，点 $E$ 在边 $A B$ 上，过点 $D$ 作 $D F ⊥ D E$ 交边 $A C$ 于点 $F$ ，连接 $E F$ 。已知 $B E = 4$ ， $C F = 5$ ，求 $E F$ 的长.

查看试题解析