河南省信阳市淮滨一中2021年中考数学模拟试试卷
试卷更新日期:2022-03-15 类型:中考模拟
一、单选题
-
1. 下列计算正确的是( ).A、 B、 C、 D、2. 下列说法正确的个数是( )
①;②;③;④;⑤的平方根是.
A、0个 B、1个 C、2个 D、3个3. 在下列多项式中,没有公因式可提取的是( )A、3x-4y B、3x+4xy C、4x2-3xy D、4x2+3x2y4. 方程组的解是( )A、 B、 C、 D、5. 下列方程:①;②;③;④(为已知数),其中分式方程有( )A、1个 B、2个 C、3个 D、4个6. 如图,四边形 内接于 ,点C是 的中点, ,则 的度数为( )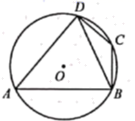 A、20° B、25° C、30° D、35°7. 如图,在 中 ,点 和 分别在 和 上,且 .连接 ,过点 的直线 与 平行,若 ,则 的度数为( )
A、20° B、25° C、30° D、35°7. 如图,在 中 ,点 和 分别在 和 上,且 .连接 ,过点 的直线 与 平行,若 ,则 的度数为( ) A、 B、 C、 D、8. 如图,在中, , , 以为边作等腰直角三角形(为直角顶点,、两点在直线的两侧),线段长的最大值为( )
A、 B、 C、 D、8. 如图,在中, , , 以为边作等腰直角三角形(为直角顶点,、两点在直线的两侧),线段长的最大值为( ) A、1 B、 C、3 D、9.
A、1 B、 C、3 D、9.如图所示的抛物线是二次函数y=ax2+bx+c(a≠0)的图象,则下列结论:
①abc>0;②b+2a=0;③抛物线与x轴的另一个交点为(4,0);④a+c>b;⑤3a+c<0.
其中正确的结论有( )
 A、5个 B、4个 C、3个 D、2个10. 如图,赵爽弦图是由四个全等的直角三角形和一个小正方形拼成的一个大正方形.设直角三角形两条直角边长分别为和 , 若 , 大正方形的边长为 , 则小正方形的面积为( )
A、5个 B、4个 C、3个 D、2个10. 如图,赵爽弦图是由四个全等的直角三角形和一个小正方形拼成的一个大正方形.设直角三角形两条直角边长分别为和 , 若 , 大正方形的边长为 , 则小正方形的面积为( ) A、9 B、3 C、12 D、13
A、9 B、3 C、12 D、13二、填空题
-
11. 如图,已知AB=12米,MA⊥AB于A,MA=6米,射线BD⊥AB于B,P点从B向A运动,每秒走1米,Q点从B向D运动,每秒走2米,P、Q同时从B出发,则出发秒后,在线段MA上有一点C,使△CAP与△PBQ全等.
 12. 若的值为正数,则得取值范围为.13. 如图,二次函数y=ax2+bx+c(a>0)图象的顶点为D,其图象与x轴的交点A、B的横坐标分别为﹣1、3,与y轴负半轴交于点C,在下面四个结论中:
12. 若的值为正数,则得取值范围为.13. 如图,二次函数y=ax2+bx+c(a>0)图象的顶点为D,其图象与x轴的交点A、B的横坐标分别为﹣1、3,与y轴负半轴交于点C,在下面四个结论中:①2a+b=0;
②c=﹣3a;
③只有当a=时,△ABD是等腰直角三角形;
④使△ACB为等腰三角形的a的值有三个.
其中正确的结论是.(请把正确结论的序号都填上)
 14. 已知A(-4,0),B(2,0),C(4,3),则△ABC的面积是.15. 如图,矩形中, , , 点在上,连接 , 以为对称轴折叠 , 得到 , 点的对应点为点 , 当点落在上时,的长为.
14. 已知A(-4,0),B(2,0),C(4,3),则△ABC的面积是.15. 如图,矩形中, , , 点在上,连接 , 以为对称轴折叠 , 得到 , 点的对应点为点 , 当点落在上时,的长为.
三、解答题
-
16. 计算.(1)、(2)、.(3)、(4)、.17. 先化简 , 再求值.其中.18.(1)、如果 , 且 , 求的值;(2)、已知、互为相反数,、互为倒数,的倒数等于它本身,则的值是多少?(3)、已知 , 求的值.19. 某学校八年级一班准备组织学生参加冬令营活动,估计人数在人之间,甲、乙旅行社的服务质量相同,且对外报价都是元/人,该班联系时,甲旅行社表示,可给予每位学生八折优惠;乙旅行社表示,可先免去三位学生的冬令营费用,其余学生九折优惠.(1)、分别写出两旅行社所报冬令营费用(元)与人数(人)的函数表达式;(2)、人数在什么范围内,选甲旅行社较划算?人数在什么范围内,选乙旅行社较划算?20. 我国是一个严重缺水的国家.为了加强公民的节水意识,某市制定了如下用水收费标准:每户每月的用水不超过8吨时,水价为每吨1.5元,超过8吨时,超过的部分按每吨2.2元收费.该市某户居民10月份用水吨,应交水费元.(1)、若 , 请写出与的函数关系式.(2)、若 , 请写出与的函数关系式.(3)、如果该户居民这个月交水费23元,那么这个月该户用了多少吨水?21. 已知抛物线的对称轴为直线 , 顶点为 , 与轴交于、两点(点在点的左侧),与轴交于点 , 且该抛物线经过点 , 联结.
 (1)、求点关于直线的对称点的坐标;(2)、联结 , 若点在直线左侧的抛物线上,且 , 求点的坐标;(3)、点在轴负半轴上,如果 , 求点的坐标.22. 如图①,直线AB与x轴负半轴、y轴正半轴分别交于A、B两点,OA、OB的长度分别为a和b,且满足a2﹣2ab+b2=0.
(1)、求点关于直线的对称点的坐标;(2)、联结 , 若点在直线左侧的抛物线上,且 , 求点的坐标;(3)、点在轴负半轴上,如果 , 求点的坐标.22. 如图①,直线AB与x轴负半轴、y轴正半轴分别交于A、B两点,OA、OB的长度分别为a和b,且满足a2﹣2ab+b2=0.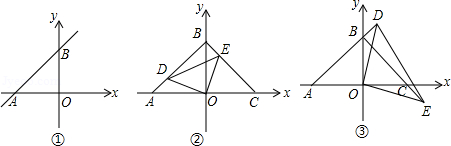 (1)、判断△AOB的形状;(2)、如图②,△COB和△AOB关于y轴对称,D点在AB上,点E在BC上,且AD=BE,试问:线段OD、OE是否存在某种确定的数量关系和位置关系?写出你的结论并证明;(3)、将(2)中∠DOE绕点O旋转,使D、E分别落在AB,BC延长线上(如图③),∠BDE与∠COE有何关系?直接说出结论,不必说明理由.
(1)、判断△AOB的形状;(2)、如图②,△COB和△AOB关于y轴对称,D点在AB上,点E在BC上,且AD=BE,试问:线段OD、OE是否存在某种确定的数量关系和位置关系?写出你的结论并证明;(3)、将(2)中∠DOE绕点O旋转,使D、E分别落在AB,BC延长线上(如图③),∠BDE与∠COE有何关系?直接说出结论,不必说明理由.

