河南省信阳市商城县2022年中招数学一模试卷
试卷更新日期:2022-03-15 类型:中考模拟
一、单选题
-
1. -2022的倒数是( )A、-2022 B、2022 C、 D、2. 下列问题中,适合抽样调查的是( )A、“双十一”期间某网店的当日销售额 B、神舟十三号飞船的零部件检查 C、“7•20”特大暴雨河南省受损的农作物面积 D、东京奥运会乒乓球比赛用球的合格率3. 下列几何体的三视图中,俯视图与主视图一定一致的是( )A、
 B、
B、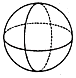 C、
C、 D、
D、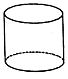 4. 如图所示,AB//CD,∠α=35°,∠C=∠D,则∠A的度数是( )
4. 如图所示,AB//CD,∠α=35°,∠C=∠D,则∠A的度数是( ) A、35° B、145° C、155° D、55°5. 新型冠状病毒呈球形或椭圆形,有包膜,直径大约是100m.新型冠状病毒是一种先前未在人类中发现的冠状病毒,显微镜下看呈皇冠形,所以称为冠状病毒.既往已知感染人的冠状病毒有六种,新型冠状病毒属于β属的冠状病毒,属于第七种冠状病毒.将100nm(1nm=10﹣9m)用科学记数法表示为( )A、1×10﹣7m B、1×10﹣8m C、1×10﹣9m D、1×10﹣6m6. 《九章算术》是中国古代数学著作之一,书中有这样的一个问题:今有甲、乙二人持钱不知其数.甲得乙半而钱五十,乙得甲太半而钱亦五十.问甲、乙持钱各几何?题意为:今有甲、乙二人,不知其钱包里有多少钱.若乙把其一半的钱给甲,则甲的钱数为50;而甲把其的钱给乙,则乙的钱数也能为50,问甲、乙各有多少钱?解:设甲原有钱数为x,乙原有钱数为y,依题意可得方程组为( )A、 B、 C、 D、7. 将分别标有“中”“国”…“全”“面”“小”“康”汉字的六个小球装在一个不透明的口袋中,这些球除汉字外无其他差别,每次摸球前先搅拌均匀,随机摸出一球,然后放回,再随机摸出一球,两次摸出的球上的汉字是“小”和“康”的概率是( )A、 B、 C、 D、8. 函数 的图象如图所示,则关于x的一元二次方程 的根的情况是( )
A、35° B、145° C、155° D、55°5. 新型冠状病毒呈球形或椭圆形,有包膜,直径大约是100m.新型冠状病毒是一种先前未在人类中发现的冠状病毒,显微镜下看呈皇冠形,所以称为冠状病毒.既往已知感染人的冠状病毒有六种,新型冠状病毒属于β属的冠状病毒,属于第七种冠状病毒.将100nm(1nm=10﹣9m)用科学记数法表示为( )A、1×10﹣7m B、1×10﹣8m C、1×10﹣9m D、1×10﹣6m6. 《九章算术》是中国古代数学著作之一,书中有这样的一个问题:今有甲、乙二人持钱不知其数.甲得乙半而钱五十,乙得甲太半而钱亦五十.问甲、乙持钱各几何?题意为:今有甲、乙二人,不知其钱包里有多少钱.若乙把其一半的钱给甲,则甲的钱数为50;而甲把其的钱给乙,则乙的钱数也能为50,问甲、乙各有多少钱?解:设甲原有钱数为x,乙原有钱数为y,依题意可得方程组为( )A、 B、 C、 D、7. 将分别标有“中”“国”…“全”“面”“小”“康”汉字的六个小球装在一个不透明的口袋中,这些球除汉字外无其他差别,每次摸球前先搅拌均匀,随机摸出一球,然后放回,再随机摸出一球,两次摸出的球上的汉字是“小”和“康”的概率是( )A、 B、 C、 D、8. 函数 的图象如图所示,则关于x的一元二次方程 的根的情况是( )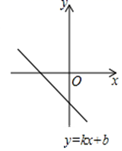 A、没有实数根 B、有两个相等的实数根 C、有两个不相等的实数根 D、无法确定9. 如图,在平面直角坐标系中放置一菱形OABC,已知∠ABC=60°,点B在y轴上,OA=1,将菱形OABC沿x轴的正方向无滑动翻转,每次翻转60°,连续翻转2021次,点B的落点依次为B1 , B2 , B3 , ……,则B2021的坐标为( )
A、没有实数根 B、有两个相等的实数根 C、有两个不相等的实数根 D、无法确定9. 如图,在平面直角坐标系中放置一菱形OABC,已知∠ABC=60°,点B在y轴上,OA=1,将菱形OABC沿x轴的正方向无滑动翻转,每次翻转60°,连续翻转2021次,点B的落点依次为B1 , B2 , B3 , ……,则B2021的坐标为( ) A、(1010,0) B、(1345,) C、( , ) D、(1346,0)10. 如图,在Rt△ABC中,∠ACB=90°,AC=BC=2 ,CD⊥AB于点D . 点P从点A出发,沿A→D→C的路径运动,运动到点C停止,过点P作PE⊥AC于点E , 作PF⊥BC于点F . 设点P运动的路程为x , 四边形CEPF的面积为y , 则能反映y与x之间函数关系的图象( )
A、(1010,0) B、(1345,) C、( , ) D、(1346,0)10. 如图,在Rt△ABC中,∠ACB=90°,AC=BC=2 ,CD⊥AB于点D . 点P从点A出发,沿A→D→C的路径运动,运动到点C停止,过点P作PE⊥AC于点E , 作PF⊥BC于点F . 设点P运动的路程为x , 四边形CEPF的面积为y , 则能反映y与x之间函数关系的图象( ) A、
A、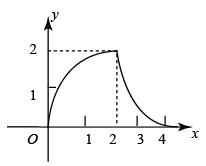 B、
B、 C、
C、 D、
D、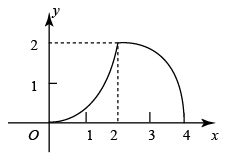
二、填空题
-
11. 请写出一个大于3小于5的无理数:.12. 某函数满足当自变量x=1时,函数值y=0.写出一个满足条件的一次函数表达式:.13. 如图所示,在△ABC中,∠B=90°,AB=BC=4,D,E,F分别是AC,BC,AB边上的点,且∠EDF=45°,DE=DF,则AF+CE=.
 14. 如图,图1是由若干个相同的图形(图2)组成的美丽图案的一部分,图2中,图形的相关数据:半径OA=2cm,∠AOB=120°.则图2的周长为cm(结果保留π).
14. 如图,图1是由若干个相同的图形(图2)组成的美丽图案的一部分,图2中,图形的相关数据:半径OA=2cm,∠AOB=120°.则图2的周长为cm(结果保留π).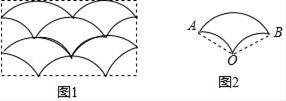 15. 在矩形ABCD中,AB=4,BC=2,点E在线段BC上,连接AE,过点B作BF⊥AE交线段CD于点F.以BE和BF为邻边作平行四边形BEHF,当点E从B运动到C时,点H运动的路径长为.
15. 在矩形ABCD中,AB=4,BC=2,点E在线段BC上,连接AE,过点B作BF⊥AE交线段CD于点F.以BE和BF为邻边作平行四边形BEHF,当点E从B运动到C时,点H运动的路径长为.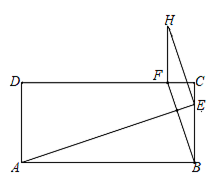
三、解答题
-
16.(1)、计算:;(2)、化简:.17. 2021年秋季教育部明确提出,要减轻义务教育阶段学生的作业负担,学生的校外培训负担.依据政策要求,初中书面作业平均完成时间不超过90分钟,学生每天的完成作业时长不能超过2小时.某中学为了积极推进教育部的新政策实施,对本校学生的作业情况进行了抽样调查,统计结果如图所示:
 (1)、这次抽样共调查了 ▲ 名学生,并补全条形统计图;(2)、计算扇形统计图中表示作业时长为2.5小时对应的扇形圆心角度数;(3)、若该中学共有学生3000人,请据此估计该校学生的作业时间不少于2小时的学生人数;(4)、通过本次调查,你认为该学校作业布置是否满足教育部的“双减”政策要求?请说明理由,并给出相应的建议.18. 弦切角定理(弦切角等于它所夹的弧所对的圆周角)在证明角相等、线段相等、线段成比例等问题时,有非常重要的作用,为了说明弦切角定理的正确性,小明同学进行了以下探索过程:
(1)、这次抽样共调查了 ▲ 名学生,并补全条形统计图;(2)、计算扇形统计图中表示作业时长为2.5小时对应的扇形圆心角度数;(3)、若该中学共有学生3000人,请据此估计该校学生的作业时间不少于2小时的学生人数;(4)、通过本次调查,你认为该学校作业布置是否满足教育部的“双减”政策要求?请说明理由,并给出相应的建议.18. 弦切角定理(弦切角等于它所夹的弧所对的圆周角)在证明角相等、线段相等、线段成比例等问题时,有非常重要的作用,为了说明弦切角定理的正确性,小明同学进行了以下探索过程:问题的提出:若一直线与圆相交,过交点作圆的切线,则此切线与直线的交角中的任意一个称为直线和圆的交角,其中所夹弧为劣弧的角为劣交角,所夹弧为优弧的角为优交角.直线和圆的交角有以下性质:直线和圆的交角等于所夹弧所对的圆周角.
问题的证明:(只证明劣交角即可)
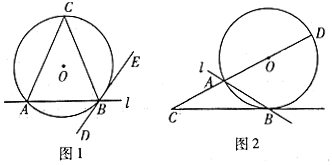 (1)、请将不完整的已知和求证补充完整,并写出证明过程;
(1)、请将不完整的已知和求证补充完整,并写出证明过程;已知:如图1,直线l与⊙O相交于点A,B,过点B作 ▲ .
求证:∠ABD= ▲ .
(2)、如图2,直线l与⊙O相交于点A,B,AD为⊙O的直径,BC切⊙O于点B,交DA的延长线于点C,若AD=BC,AC=2,求⊙O的半径.19. 如图,点P为函数与函数图象的交点,点P的纵坐标为4,轴,垂足为点B. (1)、求m的值;(2)、点M是函数图象上一动点,过点M作于点D,若 , 求点M的坐标.20. 某汽车贸易公司销售A,B两种型号的新能源汽车,A型车进货价格为每台12万元,B型车进货价格为每台15万元,该公司销售2台A型车和5台B型车,可获利3.1万元,销售1台A型车和2台B型车,可获利1.3万元.(1)、求销售一台A型、一台B型新能源汽车的利润各是多少万元?(2)、该公司准备用300万元资金,采购A,B两种新能源汽车,可能有多少种采购方案?(3)、该公司准备用不超过300万,采购A,B两种新能源汽车共22台,问最少需要采购A型新能源汽车多少台?21. 小明根据学习函数的经验,对函数y=|x2﹣2x|﹣2的图象与性质进行了探究,下面是小明的探究过程,请补充完整:
(1)、求m的值;(2)、点M是函数图象上一动点,过点M作于点D,若 , 求点M的坐标.20. 某汽车贸易公司销售A,B两种型号的新能源汽车,A型车进货价格为每台12万元,B型车进货价格为每台15万元,该公司销售2台A型车和5台B型车,可获利3.1万元,销售1台A型车和2台B型车,可获利1.3万元.(1)、求销售一台A型、一台B型新能源汽车的利润各是多少万元?(2)、该公司准备用300万元资金,采购A,B两种新能源汽车,可能有多少种采购方案?(3)、该公司准备用不超过300万,采购A,B两种新能源汽车共22台,问最少需要采购A型新能源汽车多少台?21. 小明根据学习函数的经验,对函数y=|x2﹣2x|﹣2的图象与性质进行了探究,下面是小明的探究过程,请补充完整:x
…
﹣2
﹣1
0
1
2
3
4
…
y
…
6
m
﹣2
﹣1
﹣2
n
6
…
 (1)、在给定的平面直角坐标系中;画出这个函数的图象,
(1)、在给定的平面直角坐标系中;画出这个函数的图象,①列表,其中m= ▲ , n= ▲ .
②描点:请根据表中数据,在如图所示的平面直角坐标系中描点:
③连线:画出该函数的图象.
(2)、写出该函数的两条性质:.(3)、进一步探究函数图象,解决下列问题:①若平行于x轴的一条直线y=k与函数y=|x2﹣2x|﹣2的图象有两个交点,则k的取值范围是 ;
②在网格中画出y=x﹣2的图象,直接写出方程|x2﹣2x|﹣2=x﹣2的解为 .
22. 如图,直线与x轴交于点A(3,0),与y轴交于点B,抛物线经过点A,B. (1)、求点B的坐标和抛物线的表达式;(2)、P(x1 , y1),Q(4,y2)两点均在该抛物线上,若y1≥y2 , 求P点的横坐标x1的取值范围;(3)、点M为直线AB上一动点,将点M沿与y轴平行的方向平移一个单位长度得到点N,若线段MN与抛物线只有一个公共点,直接写出点M的横坐标的取值范围.23. 在△ABC中,∠ACB=90°,AC=BC,点D是直线AB上的一动点(不与点A,B重合),连接CD,在CD的右侧以CD为斜边作等腰直角三角形CDE,点H是BD的中点,连接EH.
(1)、求点B的坐标和抛物线的表达式;(2)、P(x1 , y1),Q(4,y2)两点均在该抛物线上,若y1≥y2 , 求P点的横坐标x1的取值范围;(3)、点M为直线AB上一动点,将点M沿与y轴平行的方向平移一个单位长度得到点N,若线段MN与抛物线只有一个公共点,直接写出点M的横坐标的取值范围.23. 在△ABC中,∠ACB=90°,AC=BC,点D是直线AB上的一动点(不与点A,B重合),连接CD,在CD的右侧以CD为斜边作等腰直角三角形CDE,点H是BD的中点,连接EH. (1)、如图1,当点D是AB的中点时,线段EH与AD的数量关系是 , EH与AD的位置关系是 ;(2)、如图2,当点D在边AB上且不是AB的中点时,(1)中的结论是否仍然成立?若成立,请仅就图2中的情况给出证明;若不成立,请说明理由;(3)、若AC=BC=2 , 其他条件不变,连接AE,BE.当△BCE是等边三角形时,请直接写出△ADE的面积.
(1)、如图1,当点D是AB的中点时,线段EH与AD的数量关系是 , EH与AD的位置关系是 ;(2)、如图2,当点D在边AB上且不是AB的中点时,(1)中的结论是否仍然成立?若成立,请仅就图2中的情况给出证明;若不成立,请说明理由;(3)、若AC=BC=2 , 其他条件不变,连接AE,BE.当△BCE是等边三角形时,请直接写出△ADE的面积.