江苏省徐州市2021年中考数学综合模拟试卷
试卷更新日期:2022-03-15 类型:中考模拟
一、单选题
-
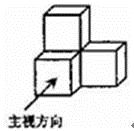
1. 化简 的结果是( )A、-2 B、 C、 D、22. 下列运算正确的是( )A、 B、 C、 D、3. 如图,是由四个相同的小正方体组成的立体图形,它的左视图是( )
 A、
A、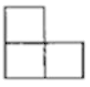 B、
B、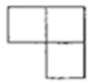 C、
C、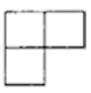 D、
D、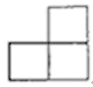 4. 一个等腰三角形有两条边的长分别为2,5,则这个等腰三角形的周长为( )A、9 B、12 C、9或12 D、9或105. 王刚是一名职业足球队员,根据以往比赛数据统计,王刚的进球率为20%,他明天将参加一场比赛,下面几种说法正确的是( )A、王刚明天的进球率为20% B、王刚明天每射球20次必进球1次 C、王刚明天有可能进球 D、王刚明天肯定进球6. 已知 , 是关于的方程的两个实数根,下列结论一定正确的是( )A、 B、 C、 D、 ,7. 如图,小刚从山脚A出发,沿坡角为的山坡向上走了300米到达B点,则小刚上升了( )
4. 一个等腰三角形有两条边的长分别为2,5,则这个等腰三角形的周长为( )A、9 B、12 C、9或12 D、9或105. 王刚是一名职业足球队员,根据以往比赛数据统计,王刚的进球率为20%,他明天将参加一场比赛,下面几种说法正确的是( )A、王刚明天的进球率为20% B、王刚明天每射球20次必进球1次 C、王刚明天有可能进球 D、王刚明天肯定进球6. 已知 , 是关于的方程的两个实数根,下列结论一定正确的是( )A、 B、 C、 D、 ,7. 如图,小刚从山脚A出发,沿坡角为的山坡向上走了300米到达B点,则小刚上升了( )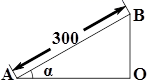 A、米 B、米 C、米 D、米8. 如图,将矩形ABCD的四个角向内翻折后,恰好拼成一个无缝隙无重叠的四边形EFGH,EH=12厘米,EF=16厘米,则边AD的长是( )
A、米 B、米 C、米 D、米8. 如图,将矩形ABCD的四个角向内翻折后,恰好拼成一个无缝隙无重叠的四边形EFGH,EH=12厘米,EF=16厘米,则边AD的长是( )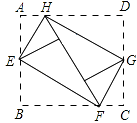 A、12厘米 B、16厘米 C、20厘米 D、28厘米
A、12厘米 B、16厘米 C、20厘米 D、28厘米二、填空题
-
9. - 的立方根是 .10. 亚洲陆地面积约为 万平方千米,将 用科学记数法表示为.11. 若在实数范围内有意义,则的取值范围是.12. 分解因式:x3-x= .13. 已知3x﹣y=3a2﹣6a+9,x+y=a2+6a﹣9,若x≤y,则实数a的值为 .
14. 已知关于x的一元二次方程mx2+5x+m2﹣2m=0有一个根为0,则m= .15. 如图,中, , 相交于点 , 若 , , 则的周长为. 16. 如图:四边形ABCD内接于⊙O,E为BC延长线上一点,若∠A=72°,则∠DCE=°.
16. 如图:四边形ABCD内接于⊙O,E为BC延长线上一点,若∠A=72°,则∠DCE=°. 17. 如图,正方形内接于圆 , , 则图中阴影部分的面积是.
17. 如图,正方形内接于圆 , , 则图中阴影部分的面积是.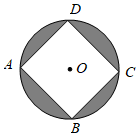 18. 如图,在平面直角坐标系中,等腰直角三角形的直角边在轴上,点在第一象限,且 , 以点为直角顶点,为一直角边作等腰直角三角形 , 再以点为直角顶点,为直角边作等腰直角三角形依此规律,则点的坐标是.
18. 如图,在平面直角坐标系中,等腰直角三角形的直角边在轴上,点在第一象限,且 , 以点为直角顶点,为一直角边作等腰直角三角形 , 再以点为直角顶点,为直角边作等腰直角三角形依此规律,则点的坐标是.
三、解答题
-
19.(1)、计算:π0+2cos30°﹣|2﹣|﹣()﹣2;(2)、化简:(2﹣)÷.20.(1)、解方程:;(2)、解不等式组:.21. 泰州具有丰富的旅游资源,小明利用周日来泰州游玩,上午从 , 两个景点中任意选择一个游玩,下午从 、 、 三个景点中任意选择一个游玩,用列表或画树状图的方法列出所有等可能的结果.并求小明恰好选中景点 和 的概率.22. 某中学数学兴趣小组为了了解本校学生的年龄情况,随机调查了该校部分学生的年龄,整理数据并绘制如下不完整的统计图.依据以上信息解答以下问题:
 (1)、该调查的样本容量是 ;(2)、补全条形统计图;(3)、若该校一共有2800名学生,估计该校年龄在15岁及以上的学生人数.23. 如图, , , 、 相交于点 .求证: .
(1)、该调查的样本容量是 ;(2)、补全条形统计图;(3)、若该校一共有2800名学生,估计该校年龄在15岁及以上的学生人数.23. 如图, , , 、 相交于点 .求证: . 24. 为了改善生态环境,某乡村计划植树4000棵.由于志题者的支援,实际工作效率提高了20%,结果比原计划提前3天完成,并且多植树80棵,原计划植树多少天?25. 如图,AB为⊙O的直径,C为⊙O上一点,∠ABC的平分线交⊙O于点D,DE⊥BC于点E.
24. 为了改善生态环境,某乡村计划植树4000棵.由于志题者的支援,实际工作效率提高了20%,结果比原计划提前3天完成,并且多植树80棵,原计划植树多少天?25. 如图,AB为⊙O的直径,C为⊙O上一点,∠ABC的平分线交⊙O于点D,DE⊥BC于点E. (1)、试判断DE与⊙O的位置关系,并说明理由;(2)、过点D作DF⊥AB于点F,若BE=3 ,DF=3,求图中阴影部分的面积.26. 如图是小红在一次放风筝活动中某时段的示意图,她在A处时的风筝线(整个过程中风筝线近似地看作直线)与水平线构成30°角,线段AA1表示小红身高1.5米.
(1)、试判断DE与⊙O的位置关系,并说明理由;(2)、过点D作DF⊥AB于点F,若BE=3 ,DF=3,求图中阴影部分的面积.26. 如图是小红在一次放风筝活动中某时段的示意图,她在A处时的风筝线(整个过程中风筝线近似地看作直线)与水平线构成30°角,线段AA1表示小红身高1.5米.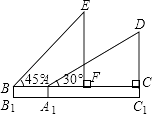 (1)、当风筝的水平距离AC=18米时,求此时风筝线AD的长度;
(1)、当风筝的水平距离AC=18米时,求此时风筝线AD的长度;
(2)、当她从点A跑动9 米到达点B处时,风筝线与水平线构成45°角,此时风筝到达点E处,风筝的水平移动距离CF=10 米,这一过程中风筝线的长度保持不变,求风筝原来的高度C1D.
27. 对给定的一张矩形纸片 进行如下操作:先沿 折叠,使点 落在 边上(如图①),再沿 折叠,这时发现点 恰好与点 重合(如图②). (1)、根据以上操作和发现,求 的值;
(1)、根据以上操作和发现,求 的值;
(2)、将该矩形纸片展开.①如图③,折叠该矩形纸片,使点 与点 重合,折痕与 相交于点 ,再将该矩形纸片展开,求证: .
②不借助工具,利用图④探索一种新的折叠方法,找出与图③中位置相同的 点,要求只有一条折痕,且点 在折痕上,请简要说明折叠方法.(不需说明理由)
28. 如图:在平面直角坐标系中,直线l:y=x﹣与x轴交于点A,经过点A的抛物线y=ax2﹣3x+c的对称轴是x=. (1)、求抛物线的解析式;(2)、平移直线l经过原点O,得到直线m,点P是直线m上任意一点,PB⊥x轴于点B,PC⊥y轴于点C,若点E在线段OB上,点F在线段OC的延长线上,连接PE,PF,且PF=3PE,求证:PE⊥PF;(3)、若(2)中的点P坐标为(6,2),点E是x轴上的点,点F是y轴上的点,当PE⊥PF时,抛物线上是否存在点Q,使四边形PEQF是矩形?如果存在,请求出点Q的坐标,如果不存在,请说明理由.
(1)、求抛物线的解析式;(2)、平移直线l经过原点O,得到直线m,点P是直线m上任意一点,PB⊥x轴于点B,PC⊥y轴于点C,若点E在线段OB上,点F在线段OC的延长线上,连接PE,PF,且PF=3PE,求证:PE⊥PF;(3)、若(2)中的点P坐标为(6,2),点E是x轴上的点,点F是y轴上的点,当PE⊥PF时,抛物线上是否存在点Q,使四边形PEQF是矩形?如果存在,请求出点Q的坐标,如果不存在,请说明理由.