吉林省吉林市永吉县2020-2021学年七年级下学期期中考试数学试题

试卷更新日期：2022-03-15 类型：期中考试

进入出卷网下载

一、单选题

1. 下列各图中，∠1和∠2是对顶角的是（）

A、 B、 C、 D、

查看试题解析
2. 如图所示，四幅汽车标志设计中，能通过平移得到的是（）

A、 B、 C、 D、

查看试题解析
3. 式子 $\sqrt{(- 2)^{2}}$ 的值为（）

A、4 B、 $- 4$ C、 $2$ D、 $- 2$

查看试题解析
4. 在-3.14， $\sqrt{2}$ ， 0， $π$ ， $\frac{22}{7}$ ， $\sqrt{16}$ ， 0.1010010001…中，无理数的个数有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
5. 如图，点E在BA的延长线上，点F在BD的延长线上．下列选项中能判定AB∥CD的是（）

A、∠1＝∠2 B、∠3＝∠4 C、∠5＝∠B D、∠6＝∠C

查看试题解析

二、填空题

6. $\sqrt[3]{- 64}$ 的相反数是．

查看试题解析
7. 如图，AB与DE相交于点O，OC⊥AB，∠AOE＝55° ，则∠COD的度数是．

查看试题解析
8. 在平面直角坐标系中，若点A（－3，a）在第二象限，则点B（5，－a）第象限．

查看试题解析
9. 在平面直角坐标系中，点A（m，n）在第三象限，则m＋n的值可以是（写出满足条件的一个值即可）．

查看试题解析
10. 如图，某单位要在河岸 $l$ 上建一个水泵房引水到C处，他们的做法是：过点C作 $C D ⊥ l$ 于点D，将水泵房建在了D处．这样做最节省水管长度，其数学道理是．

查看试题解析
11. 如图，若点A的坐标为（1，2），若点B的坐标为（-2，1），则点C的坐标为．

查看试题解析
12. 若点A（m-1，m+2）在x轴上，则点A的坐标为．

查看试题解析
13. 长方形OABC在平面直角坐标系中的位置如图所示，其中的三个顶点分别为O（0，0），A（5，0），C（0，3）．将长方形OABC沿x轴向右平移3个单位长度，得到长方形O₁A₁B₁C₁ ，则长方形O₁A₁B₁C₁与长方形OABC重合部分的周长为．

查看试题解析

三、解答题

14. 计算： $\sqrt{25} + \sqrt[3]{27} - \sqrt{\frac{4}{9}}$ ．

查看试题解析
15. 如图，O为直线AB上一点，OC⊥AB，并且∠AOD＝130°．求∠COD的度数．

查看试题解析
16. 在平面直角坐标系中，已知O，A，B，C四点的坐标分别为O（0，0），A（0，3），B（－3，3），C（－3，0）．

(1)、在平面直角坐标系中，描出O，A，B，C四点；

(2)、依次连接OA，AB，BC，CO后，得到图形的形状是．

查看试题解析
17. 如图，直线a和直线b被直线c，d所截，若∠1＝70°，∠2＝70°，∠3＝80°．求∠4的度数．

查看试题解析
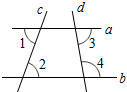18. 如图所示，点P是∠AOB的OA边上一点．

(1)、过点P作CD∥OB（C，D两点分别在OA的左、右两侧），作PE⊥OB，垂足为E；

(2)、若∠O＝65°，则∠OPE的度数是， ∠OPC的度数是， ∠APE的度数是．

查看试题解析
19. 若8的立方根是a，b的算术平方根是3，m的两个平方根分别是5和n．

(1)、求 $b - \frac{27}{8} a$ 的平方根；

(2)、求 $5 a + b - m - n$ 的立方根．

查看试题解析
20. 如图，DG∥AB，∠1＝∠2，EF⊥AC于F，判断BD与AC的位置关系，并说明理由．

查看试题解析
21. 如图，E为DF上的一点，B为AC上一点，如果∠1＝∠2，∠C＝∠D．
求证：DF∥AC．
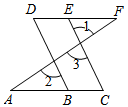
以下是小明同学的证明过程，请你帮他完成填空：
证明：∵∠1＝∠2（已知），
又∵∠1＝∠3（                  ▲                  ），
∴∠2＝                  ▲                  （等量代换）．
∴                  ▲                  ∥                  ▲                  （                  ▲                  ）．
∴∠C＝∠ABD （                  ▲                  ）．
∵∠C＝∠D（已知），
∴∠D＝∠ABD（等量代换）．
∴DF∥AC（                  ▲                  ）．

查看试题解析
22. 已知，如图，BC与DE相交于点O，给出下面三个论断：①∠B＝∠E；②AB∥DE；③BC∥EF．请以其中的两个论断为条件，填入“题设”栏中；剩下的论断为结论，填入“结论”栏中，使之成为一个真命题，并加以证明．
题设：已知：如图，BC与DE相交于点O， ▲ ， ▲ （填序号）．
结论： ▲ （填序号）．
证明：

查看试题解析
23. 根据下表回答下列问题：
x
16
16.1
16.2
16.3
16.4
16.5
16.6
16.7
16.8
16.9
17
x²
256
159.21
262.44
265.69
268.96
272.25
275.56
278.89
282.24
285.62
289

(1)、289的算术平方根是， $\sqrt{268.96}$ ＝；

(2)、 $\pm \sqrt{256}$ ＝， 275.56的平方根是；

(3)、 $\sqrt{1.5921}$ ＝， $\sqrt{28224}$ ＝；

(4)、若 $\sqrt{x} = a$ （x＞0），则 $\sqrt{100 x}$ ＝（用含a的式子表示）．

查看试题解析
24. 在平面直角坐标系中，点A的坐标为（2，a），点B的坐标为（b，－4），点C的坐标为（c，0），并且a，b，c满足 $(a + 4)^{2} + | b - 5 | + \sqrt{c - 4} = 0$ ．

(1)、a＝， b＝， c＝，在平面直角坐标系中，画出△ABC；

(2)、求△ABC的面积S；

(3)、把△ABC向上平移2个单位长度，再向左平移4个单位长度，得到△A₁B₁C₁ ，直接画出平移后的△A₁B₁C₁（点A的对应点是A₁ ，点B的对应点是B₁ ，点C的对应点是C₁），点B₁的坐标为．

查看试题解析
25. 阅读下面文字：
我们知道： $\sqrt{2}$ 是无理数，而无理数是无限不循环小数，因此 $\sqrt{2}$ 的小数部分我们不可能全部写出来，于是小明用 $\sqrt{2} - 1$ 来表示 $\sqrt{2}$ 的小数部分，事实上小明的表示法是有道理的，因为 $\sqrt{2}$ 的整数部分是1，将这个数减去其整数部分，差就是小数部分．又例如：由“平方与开平方互为逆运算”可知： $2^{2}$ ＜ $(\sqrt{7})^{2}$ ＜ $3^{2}$ ，即 $2 ＜ \sqrt{7} ＜ 3$ ， ∴ $\sqrt{7}$ 的整数部分是2，小数部分是 $\sqrt{7} - 2$ ．

(1)、 $\sqrt{10}$ 的整数部分是，小数部分是；

(2)、如果 $\sqrt{5}$ 的小数部分是a， $\sqrt{37}$ 整数部分是b，求 $b - a + 2 \sqrt{5}$ 的值；

(3)、已知 $10 + \sqrt{3} = x + y$ ，其中x是整数，且 $0 ＜ y ＜ 1$ ，求 $| y - x |$ ．

查看试题解析

x	16	16.1	16.2	16.3	16.4	16.5	16.6	16.7	16.8	16.9	17
x²	256	159.21	262.44	265.69	268.96	272.25	275.56	278.89	282.24	285.62	289