吉林省白山市长白朝鲜族自治县2020-2021学年七年级下学期期中数学试题
试卷更新日期:2022-03-15 类型:期中考试
一、单选题
-
1. 下列四个实数中,是无理数的是( )A、 B、3.1415 C、 D、2. 通过估算,估计 的大小应在( )A、7~8之间 B、8.0~8.5之间 C、8.5~9.0之间 D、9~10之间3.
如图,把一块含有45°角的直角三角板的两个顶点放在直尺的对边上.如果∠1=20°,那么∠2的度数是( )
 A、30° B、25° C、20° D、15°4.
A、30° B、25° C、20° D、15°4.如图,在5×5方格纸中,将图①中的三角形甲平移到图②中所示的位置,与三角形乙拼成一个矩形,那么,下面的平移方法中,正确的是( )
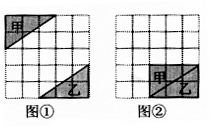 A、先向下平移3格,再向右平移1格 B、先向下平移2格,再向右平移1格 C、先向下平移2格,再向右平移2格 D、先向下平移3格,再向右平移2格5. 如图,若在象棋盘上建立直角坐标系,使“帅”位于点 .“馬”位于点 ,则“兵”位于点( )
A、先向下平移3格,再向右平移1格 B、先向下平移2格,再向右平移1格 C、先向下平移2格,再向右平移2格 D、先向下平移3格,再向右平移2格5. 如图,若在象棋盘上建立直角坐标系,使“帅”位于点 .“馬”位于点 ,则“兵”位于点( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
6. 的相反数是 .7. 27的立方根为 .8. 剧院里5排2号可以用(5,2)表示,则7排4号用表示。
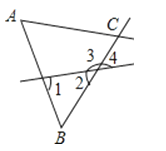
9.如图,有下列判断:①∠A与∠1是同位角;②∠A与∠B是同旁内角;③∠4与∠1是内错角;④∠1与∠3是同位角. 其中正确的是(填序号).
 10. 一大门的栏杆如图所示,BA垂直地面AE于点A,CD平行于地面AE,则∠ABC+∠BCD=.
10. 一大门的栏杆如图所示,BA垂直地面AE于点A,CD平行于地面AE,则∠ABC+∠BCD=. 11. 第二象限内的点P(x,y)满足|x|=9,y2=4,则点P的坐标是 .12. 如图,观察所给算式,找出规律:
11. 第二象限内的点P(x,y)满足|x|=9,y2=4,则点P的坐标是 .12. 如图,观察所给算式,找出规律:1+2+1=4,
1+2+3+2+1=9,
1+2+3+4+3+2+1=16,
1+2+3+4+5+4+3+2+1=25,
……
根据规律计算1+2+3+…+99+100+99+…+3+2+1=
13. 在平面直角坐标系 中,对于点 我们把 叫做点P的伴随点,已知 的伴随点为 ,点 的伴随点为 ,点 的伴随点为 ,这样依次得到 ,若点 的坐标为 ,则点 的坐标为三、解答题
-
14. 计算:15. 已知:如图, , , 说明 . 请你补全推理过程和空缺的推理依据.
解:∵(已知),
∴ ▲ ( ▲ ),
又∵(已知),
∴ ▲ ( ▲ ),
∴ ▲ ( ▲ ),
∴(等量代换).
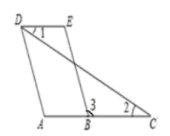 16. 一个正数x的平方根是a+3和2a﹣18,求x的立方根.17. 在平面直角坐标系中,分别根据下列条件,求出各点的坐标.(1)、点A在y轴上,位于原点上方,距离原点2个单位长度;(2)、点B在x轴上,位于原点右侧,距离原点1个单位长度;(3)、点C在x轴上方,y轴右侧,距离每条坐标轴都是2个单位长度;(4)、点D在x轴下方,y轴左侧,距离每条坐标轴都是3个单位长度;(5)、点E在x轴下方,y轴右侧,距离x轴2个单位长度,距离y轴4个单位长度.18. 如图,已知 , , 那么与相等吗?为什么?
16. 一个正数x的平方根是a+3和2a﹣18,求x的立方根.17. 在平面直角坐标系中,分别根据下列条件,求出各点的坐标.(1)、点A在y轴上,位于原点上方,距离原点2个单位长度;(2)、点B在x轴上,位于原点右侧,距离原点1个单位长度;(3)、点C在x轴上方,y轴右侧,距离每条坐标轴都是2个单位长度;(4)、点D在x轴下方,y轴左侧,距离每条坐标轴都是3个单位长度;(5)、点E在x轴下方,y轴右侧,距离x轴2个单位长度,距离y轴4个单位长度.18. 如图,已知 , , 那么与相等吗?为什么? 19. 如图.在边长为单位1的正方形网格中建立平面直角坐标系,李老师在平面直角坐标系中x轴下方画出一个 . 请同学们解答下列问题:
19. 如图.在边长为单位1的正方形网格中建立平面直角坐标系,李老师在平面直角坐标系中x轴下方画出一个 . 请同学们解答下列问题: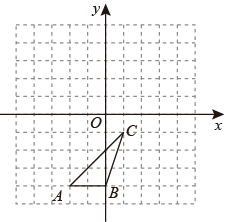 (1)、写出各顶点的坐标和的面积;(2)、画出向上平移4个单位得到的 .20.(1)、计算: , , , .
(1)、写出各顶点的坐标和的面积;(2)、画出向上平移4个单位得到的 .20.(1)、计算: , , , .根据计算结果,回答:对于任意数a, 等于多少?
(2)、利用(1)中的结论,计算: .21. 如图,在平面直角坐标系中,点为x轴负半轴上一点,点为y轴正半轴上一点,其中b满足方程 .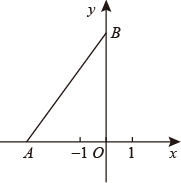 (1)、求点A,B的坐标;(2)、点C为y负半轴上一点,且的面积为12,求点C的坐标;22. 一个正数的两个平方根为 和 , 是 的立方根, 的小数部分是 ,求 的平方根.23. 【探究】如图①,∠AFH和∠CHF的平分线交于点O,EG经过点O且平行于FH,分别与AB、CD交于点E、G.
(1)、求点A,B的坐标;(2)、点C为y负半轴上一点,且的面积为12,求点C的坐标;22. 一个正数的两个平方根为 和 , 是 的立方根, 的小数部分是 ,求 的平方根.23. 【探究】如图①,∠AFH和∠CHF的平分线交于点O,EG经过点O且平行于FH,分别与AB、CD交于点E、G.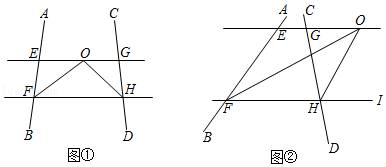 (1)、若∠AFH=60°,∠CHF=50°,则∠EOF=度,∠FOH=度.(2)、若∠AFH+∠CHF=100°,求∠FOH的度数.(3)、【拓展】如图②,∠AFH和∠CHI的平分线交于点O,EG经过点O且平行于FH,分别与AB、CD交于点E、G.若∠AFH+∠CHF=α,直接写出∠FOH的度数.(用含a的代数式表示)24. 判断下面各式是否成立(1)、 (2) (3)
(1)、若∠AFH=60°,∠CHF=50°,则∠EOF=度,∠FOH=度.(2)、若∠AFH+∠CHF=100°,求∠FOH的度数.(3)、【拓展】如图②,∠AFH和∠CHI的平分线交于点O,EG经过点O且平行于FH,分别与AB、CD交于点E、G.若∠AFH+∠CHF=α,直接写出∠FOH的度数.(用含a的代数式表示)24. 判断下面各式是否成立(1)、 (2) (3)探究:①你判断完上面各题后,发现了什么规律?并猜想: ▲
②用含有n的代数式将规律表示出来,说明n的取值范围,并给出证明
25. 在综合与实践课上,老师让同学们以“三条平行线m,n,l(即始终满足m∥n∥l)和一副直角三角尺ABC,DEF(∠BAC=∠EDF=90°,∠FED=60°,∠DFE=30°,∠ABC=∠ACB=45°)”为主题开展数学活动.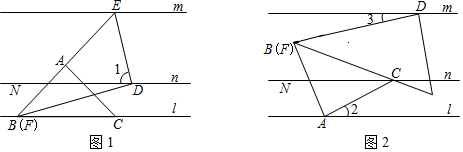
操作发现
(1)、如图1,展翅组把三角尺ABC的边BC放在l上,三角尺DEF的顶点F与顶点B重合,边EF经过AB,顶点E恰好落在m上,顶点D恰好落在n上,边ED与n相交所成的一个角记为∠1,求∠1的度数;(2)、如图2,受到展翅组的启发,高远组把直线m向下平移后使得两个三角尺的两个直角顶点A、D分别落在m和l上,顶点C恰好落在n上,边AC与l相交所成的一个角记为∠2,边DF与m相交所成的一个角记为∠3,请你说明∠2﹣∠3=15°;结论应用
(3)、老师在点评高远组的探究操作时提出,在(2)的条件下,若点N是直线n上一点,CN恰好平分∠ACB时,∠2与∠3之间存在一个特殊的倍数关系,请你直接写出它们之间的倍数关系,不需要说明理由.