黑龙江省佳木斯市2020-2021学年七年级下学期期中数学试题
试卷更新日期:2022-03-15 类型:期中考试
一、单选题
-
1. 下列计算正确的是( )A、 B、 C、 D、2. 如图所示的图案分别是四种汽车的车标,其中可以看作是由“基本图案”经过平移得到的是( )A、
 B、
B、 C、
C、 D、
D、 3. 如果电影票上的“5排2号”记作(5,2),那么(4,3)表示( )A、3排5号 B、5排3号 C、4排3号 D、3排4号4.
3. 如果电影票上的“5排2号”记作(5,2),那么(4,3)表示( )A、3排5号 B、5排3号 C、4排3号 D、3排4号4.如图所示,在灌溉农田时,要把河(直线l表示一条河)中的水引到农田P处,设计了四条路线PA,PB,PC,PD(其中PB⊥l),你选择哪条路线挖渠才能使渠道最短( )
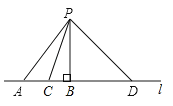 A、PA B、PB C、PC D、PD5. 在实数3.14159, , , 4.21, , 中,无理数的个数有( )A、1个 B、2个 C、3个 D、4个6. 线段MN在直角坐标系中的位置如图所示,线段M1N1与MN关于y轴对称,则点M的对应的点M1的坐标为( )
A、PA B、PB C、PC D、PD5. 在实数3.14159, , , 4.21, , 中,无理数的个数有( )A、1个 B、2个 C、3个 D、4个6. 线段MN在直角坐标系中的位置如图所示,线段M1N1与MN关于y轴对称,则点M的对应的点M1的坐标为( )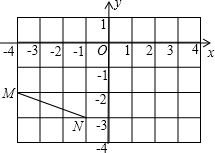 A、(4,2) B、(-4,2) C、(-4,-2) D、(4,-2)7. 如图,能判定的条件是( )
A、(4,2) B、(-4,2) C、(-4,-2) D、(4,-2)7. 如图,能判定的条件是( ) A、 B、 C、 D、8. 当a<0时,-a的平方根是( )A、a B、 C、 D、9. 点B(m2+1,-1)一定在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限10. 如图, , 于点 , 于点 , 关于下列结论:①;②;③点到的距离是线段;④;⑤如果 , 那么 . 其中结论正确的序号为( )
A、 B、 C、 D、8. 当a<0时,-a的平方根是( )A、a B、 C、 D、9. 点B(m2+1,-1)一定在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限10. 如图, , 于点 , 于点 , 关于下列结论:①;②;③点到的距离是线段;④;⑤如果 , 那么 . 其中结论正确的序号为( ) A、①②③ B、①⑤ C、①②③④ D、②④⑤
A、①②③ B、①⑤ C、①②③④ D、②④⑤二、填空题
-
11. 的算术平方根是12. 课间操时,小颖、小浩的位置如图所示,小明对小浩说,如果我的位置用(0,0)表示,小颖的位置用(2,1)表示,那么小浩的位置可以表示成 .
 13. 在同一平面内,4条直线的位置如图所示,已知 , 请添加一个条件 , 使(填一个即可).
13. 在同一平面内,4条直线的位置如图所示,已知 , 请添加一个条件 , 使(填一个即可).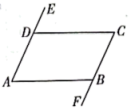 14. 如图所示,用直尺和三角尺作直线AB,CD,从图中可知,直线AB与直线CD的位置关系为 .
14. 如图所示,用直尺和三角尺作直线AB,CD,从图中可知,直线AB与直线CD的位置关系为 . 15. 将 , -3, , 按照从大到小的顺序排列为 . (用“>”连接).16. 线段是由线段经过平移得到的,若点的对应点为 , 则点的对应点的坐标是 .17. 已知 为两个连续的整数,且 ,则 = .18. 在平面直角坐标系中,点在轴上,且到原点的距离是 , 则点的坐标是 .19. 如图,∠α与∠β有共同的顶点,且它们的两边分别垂直,已知 ,那么,∠α=度,∠β=度.
15. 将 , -3, , 按照从大到小的顺序排列为 . (用“>”连接).16. 线段是由线段经过平移得到的,若点的对应点为 , 则点的对应点的坐标是 .17. 已知 为两个连续的整数,且 ,则 = .18. 在平面直角坐标系中,点在轴上,且到原点的距离是 , 则点的坐标是 .19. 如图,∠α与∠β有共同的顶点,且它们的两边分别垂直,已知 ,那么,∠α=度,∠β=度. 20. 如图,在平面直角坐标系中,三角形 , 三角形 , 三角形都是斜边在轴上,斜边长分别为2,4,6,…的等腰直角三角形.若三角形的顶点坐标分别为 , , , 则按图中规律,点的坐标为 .
20. 如图,在平面直角坐标系中,三角形 , 三角形 , 三角形都是斜边在轴上,斜边长分别为2,4,6,…的等腰直角三角形.若三角形的顶点坐标分别为 , , , 则按图中规律,点的坐标为 . 21. 如图,填空:
21. 如图,填空: (1)、若 , 则 , 理由是;(2)、若 , 则 , 理由是;(3)、若 , 则 , 理由是;(4)、若 , 则 , 理由是;(5)、若 , 则 , 理由是 .
(1)、若 , 则 , 理由是;(2)、若 , 则 , 理由是;(3)、若 , 则 , 理由是;(4)、若 , 则 , 理由是;(5)、若 , 则 , 理由是 .三、解答题
-
22. 计算:(1)、;(2)、 .23. 如图,平面直角坐标系中的网格平面是由边长为1个单位长度的小正方形组成的,线段 , , 拼接成了一个三角形,并且 , , 三点是网格线的交点,请你根据要求完成下列问题:
 (1)、将三角形先向右平移6个单位长度,再向上平移3个单位长度,平移后点和点对应,点和点对应,点和点对应,画出平移后的三角形;(2)、直接写出点 , , 的坐标;(3)、求出点在平移过程中经过的路线长度.
(1)、将三角形先向右平移6个单位长度,再向上平移3个单位长度,平移后点和点对应,点和点对应,点和点对应,画出平移后的三角形;(2)、直接写出点 , , 的坐标;(3)、求出点在平移过程中经过的路线长度.


