广东省珠海市三校联考2020-2021学年七年级下学期期中数学试题

试卷更新日期：2022-03-15 类型：期中考试

进入出卷网下载

一、单选题

1. $\sqrt{25}$ 的平方根是（）

A、 $\sqrt{5}$ B、±5 C、5 D、± $\sqrt{5}$

查看试题解析
2. 在平面直角坐标系中，点 $P (5 ， - 3)$ 在（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
3. 在下列各数中，无理数是（）

A、 $\sqrt{4}$ B、 $\frac{22}{7}$ C、 $\frac{π}{2}$ D、﹣ $\frac{2}{3}$

查看试题解析
4. 下列等式成立的是（）

A、 $\sqrt{25}$ ＝±5 B、± $\sqrt{0.36}$ ＝±0.6 C、 $\sqrt{(- 4)^{2}}$ ＝﹣4 D、 $\sqrt[3]{(- 3)^{3}}$ ＝3

查看试题解析
5. 在直角坐标系中，将点（2，﹣3）向左平移两个单位长度得到的点的坐标是（）

A、（4，﹣3） B、（﹣4，3） C、（0，﹣3） D、（0，3）

查看试题解析
6. 如图，点E在AC的延长线上，下列条件不能判断AC∥BD的是（）

A、∠3=∠4 B、∠D=∠DCE C、∠1=∠2 D、∠D+∠ACD=180°

查看试题解析
7. 如图，将直角 $Δ A B C$ 沿着点 $B$ 到点 $C$ 的方向平移到 $Δ D E F$ 的位置， $A B = 10$ ， $D O = 4$ ，平移距离为6，则阴影部分面积为（）

A、48 B、30 C、38 D、50

查看试题解析
8. 估算 $\sqrt{56}$ 的值在（）

A、5﹣6之间 B、6﹣7之间 C、7﹣8之间 D、8﹣9之间

查看试题解析
9. 线l₁∥l₂ ，一块含30°角的直角三角板如图所示放置，∠1＝25°，则∠2等于（　　）

A、30° B、35° C、40° D、45°

查看试题解析
10. 如图，在平面直角坐标系中，A（1，1），B（﹣1，1），C（﹣1，﹣2），D（1，﹣2），把一条长为2021个单位长度且没有弹性的细线（线的粗细忽略不计）的一端固定在点A处，并按A﹣B﹣C﹣D﹣A…的规律绕在四边形ABCD的边上，则细线另一端所在位置的点的坐标是（）

A、（﹣1，0） B、（0，2） C、（﹣1，﹣2） D、（0，1）

查看试题解析

二、填空题

11. 16的算术平方根是；﹣27的立方根是.

查看试题解析
12. 在实数 $\frac{1}{3}$ 、0、﹣1、﹣ $\sqrt{2}$ 中，最小的实数是．

查看试题解析
13. 将命题“对顶角相等”改为“如果…那么…”的形式为：.

查看试题解析
14. 若点A在y轴上，且到x轴的距离为3，则点A的坐标为．

查看试题解析
15. 如图，有一张四边形纸片ABCD，AD∥BC，将它沿GH折叠，点C落在点Q处，点D落在AB边上的点E处，若∠GHB＝80°，则∠AGE等于．

查看试题解析
16. 如图所示，已知∠ACB＝90°，若BC＝8cm，AC＝6cm，AB＝10cm，则点A到BC的距离是，点C到AB的距离是．

查看试题解析
17. 如图，AB∥CD，OE平分∠BOC，OF⊥OE，OP⊥CD，∠ABO＝40°，则下列结论：①∠BOE＝70°；②OF平分∠BOD；③∠1＝∠2；④∠POB＝2∠3．其中正确的结论有．（填序号）

查看试题解析

三、解答题N

18. 计算： $(- 2)^{2} + \sqrt{(- 3)^{2}} - \sqrt[3]{27} + | \sqrt{3} - 2 |$ ．

查看试题解析
19. 小明给下图建立平面直角坐标系，使医院的坐标为（0，0），火车站的坐标为（2，2）．

(1)、写出体育场、文化宫、超市、宾馆、市场的坐标；

(2)、分别指出（1）中每个场所所在象限.

查看试题解析
20. 如图所示，∠B＝∠C，AB∥CD，证明：CE∥BF.

查看试题解析
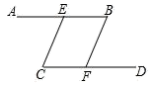21. 在平面直角坐标系xOy中，把△ABC向右平移5个单位长度，再向上平移3个单位长度，得到△A₁B₁C₁ ．

(1)、画出平移后的△A₁B₁C₁；

(2)、写出△A₁B₁C₁三个顶点A₁、B₁、C₁的坐标．

(3)、求△ABC的面积．

查看试题解析
22. 已知一个正数m的两个不相等的平方根是a+6与2a﹣9．

(1)、求a的值；

(2)、求这个正数m；

(3)、求关于x的方程ax²﹣16＝0的解．

查看试题解析
23. 如图，已知 $∠ 1 + ∠ 2 = 180^{\circ}$ ， $∠ 3 = ∠$ B.

(1)、试判断DE与BC的位置关系，并说明理由 $；$

(2)、若DE平分 $∠ A D C$ ， $∠ 2 = 3 ∠ B$ ，求 $∠ 1$ 的度数.

查看试题解析
24. 先观察下列各式： $\sqrt{1} = 1$ ； $\sqrt{1 + 3} = \sqrt{4} = 2$ ； $\sqrt{1 + 3 + 5} = \sqrt{9} = 3$ ； $\sqrt{1 + 3 + 5 + 7} = \sqrt{16} = 4$ ；

(1)、计算： $\sqrt{1 + 3 + 5 + 7 + 9 + 11} =$ ；

(2)、已知 $n$ 为正整数，通过观察并归纳，请写出： $\sqrt{1 + 3 + 5 + 7 + 9 + 11 + \dots + (2 n - 1)} =$ ；

(3)、应用上述结论，请计算 $\sqrt{4 + 12 + 20 + 28 + 36 + 44 + \dots + 204}$ 的值.

查看试题解析
25. 如图，已知点 $A (a ， 0) 、 B (b ， 0)$ 满足 ${(3 a + b)}^{2} + | b - 3 | = 0$ ．将线段 $A B$ 先向上平移2个单位，再向右平移1个单位后得到线段 $C D$ ，并连接 $A C 、 B D$ ．

(1)、请求出点 $A$ 和点 $B$ 的坐标；

(2)、点 $M$ 从 $O$ 点出发，以每秒1个单位的速度向上平移运动．设运动时间为 $t$ 秒，问：是否存在这样的 $t$ ，使得四边形 $O M D B$ 的面积等于8？若存在，请求出 $t$ 的值：若不存在，请说明理由；

(3)、在（2）的条件下，点 $M$ 从 $O$ 点出发的同时，点 $N$ 从点 $B$ 出发，以每秒2个单位的速度向左平移运动，设射线 $D N$ 交 $y$ 轴于点 $E$ ．设运动时间为 $t$ 秒，问： $S_{Δ E M D} - S_{Δ O E N}$ 的值是否会发生变化？若不变，请求出它的值：若变化，请说明理由．

查看试题解析