广东省深圳市三校联考2020-2021学年七年级下学期期中数学试题

试卷更新日期：2022-03-15 类型：期中考试

进入出卷网下载

一、单选题

1. 图中的∠1、∠2可以是对顶角的是（）

A、 B、 C、 D、

查看试题解析
2. 下列计算正确的是（　　）

A、a＋2a²＝3a² B、a⁸÷a²＝a⁴ C、a³·a²＝a⁶ D、(a³)²＝a⁶

查看试题解析
3. 多项式a²+b²与a²﹣b²的差是（）

A、0 B、2b² C、﹣2b² D、﹣2a²

查看试题解析
4. 如果三角形的两边长分别为2和6，第三边长为偶数，那么这个三角形的周长可以是（）

A、6 B、13 C、14 D、15

查看试题解析
5. 如图，从旗杆AB的顶端A向地面拉一条绳子，绳子底端恰好在地面P处，若旗杆的高度为3.2米，则绳子AP的长度不可能是（）

A、3 B、3.3 C、4 D、5

查看试题解析
6. 如图，下列判断正确的是（）

A、若 $∠ 1 = ∠ 2$ ，则 $A B / / C D$ B、若 $∠ 1 = ∠ 2$ ，则 $A D / / B C$ C、若 $∠ A = ∠ 3$ ，则 $A D / / B C$ D、若 $∠ A + ∠ A B C = 180 °$ ，则 $A B / / C D$

查看试题解析
7. 一个蓄水池有水50m³ ，打开放水闸门放水，水池里的水和放水时间的关系如表，下面说法不正确的是（）
放水时间（分）
1
2
3
4
…
水池中水量（m³）
48
46
44
42
…

A、水池里的水量是自变量，放水时间是因变量 B、每分钟放水2m³ C、放水10分钟后，水池里还有水30m³ D、放水25分钟，水池里的水全部放完

查看试题解析
8. 一水池放水，先用一台抽水机工作一段时间后停止，然后再调来一台同型号抽水机，剩下的水量为s．下面能反映s与t之间的关系的大致图象是（）

A、 B、 C、 D、

查看试题解析
9. 如图，已知长方形纸片ABCD，点E，点F，G在BC边上，GH折叠，使点B和点C都落在点P处，若∠BFE+∠CGH＝118°，则∠FPG的度数为（）

A、54° B、55° C、56° D、57°

查看试题解析
10. 观察下列各式及其展开式
（a+b）²＝a²+2ab+b²

（a+b）³＝a³+3a²b+3ab²+b³

（a+b）⁴＝a⁴+4a³b+6a²b²+4ab³+b⁴

（a+b）⁵＝a⁵+5a⁴b+10a³b²+10a²b³+5ab⁴+b⁵

……

请你猜想（2x﹣1）⁸的展开式中含x²项的系数是（）

A、224 B、180 C、112 D、48

查看试题解析

二、填空题

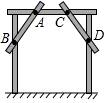
11. 赵师傅在做完门框后，为防止变形，如图中所示的那样在门上钉上两条斜拉的木条（即图中的AB，CD），这其中的数学原理是．

查看试题解析
12. 若 $4 x^{2} - (k - 1) x + 16$ 是完全平方式，则 $k =$ ．

查看试题解析
13. 初2021级某班班树现在高60厘米，以后每个月长高2厘米，x月后这棵树的高度为h厘米．

查看试题解析
14. 如图，将一副三角板叠放在一起，使直角顶点重合于O，求∠AOC+∠BOD= ．

查看试题解析
15. 甲、乙两人骑车从学校出发，先上坡到距学校6千米的A地，再下坡到距学校16千米的B地（千米）与时间x（小时）之间的函数关系如图所示.若甲、乙同时从B地按原路返回学校，返回时，甲和乙上、下坡的速度仍保持不变，则在返回途中二人相遇时离A地的距离是千米．

查看试题解析

三、解答题

16. 先化简，在求值：
$(- a + b) (- a - b) + (8 a b^{3} - 8 a^{2} b^{2}) \div 4 a b$ ，其中 $a = 2020$ ， $b = 2019$ .

查看试题解析
17. 如图，在△ABC中，∠ACB＝60°，∠BAC=75°，AD⊥BC于D，BE⊥AC于E，求∠CHD的度数．

查看试题解析
18. 如图，已知DC//FP，∠1＝∠2，∠AGF＝80°，∠DEF＝30°，FH平分∠EFG．

(1)、说明：DC//AB；

(2)、求∠PFH的度数．

查看试题解析
19. 阅读下面的材料并填空：
①（1﹣ $\frac{1}{2}$ ）（1+ $\frac{1}{2}$ ）＝1﹣ $\frac{1}{2^{2}}$ ，反过来，得1﹣ $\frac{1}{2^{2}}$ ＝（1﹣ $\frac{1}{2}$ ）（1+ $\frac{1}{2}$ ）＝ $\frac{1}{2}$ × $\frac{3}{2}$ ；
②（1﹣ $\frac{1}{3}$ ）（1+ $\frac{1}{3}$ ）＝1﹣ $\frac{1}{3^{2}}$ ，反过来，得1﹣ $\frac{1}{3^{2}}$ ＝（1﹣ $\frac{1}{3}$ ）（1+ $\frac{1}{3}$ ）＝ ▲ × ▲ ；
③（1﹣ $\frac{1}{4}$ ）（1+ $\frac{1}{4}$ ）＝1﹣ $\frac{1}{4^{2}}$ ，反过来，得1﹣ $\frac{1}{4^{2}}$ ＝ ▲ ＝ $\frac{3}{4} \times \frac{5}{4}$ ；
利用上面的材料中的方法和结论计算下题：
（1﹣ $\frac{1}{2^{2}}$ ）（1﹣ $\frac{1}{3^{2}}$ ）（1﹣ $\frac{1}{4^{2}}$ ）……（1﹣ $\frac{1}{201 6^{2}}$ ）（1﹣ $\frac{1}{201 7^{2}}$ ）（1﹣ $\frac{1}{201 8^{2}}$ ）.

查看试题解析
20. 某移动通讯公司开设两种业务（1）“全球通”：先缴50元月租费，然后每通话1分钟，再付话费0.4元；（2）“神州行”：不缴纳月租费，每通话1分钟（通话均指市话）付费0.6元．若设一个月内通话x分钟，两种业务的费用分别为y₁和y₂元（通话时不足1分钟的按1分钟计算，如3分20秒按4分钟收费）．

(1)、写出y₁、y₂与x之间的函数关系式；

(2)、一个月内通话多少分钟，两种费用相同？

(3)、某人估计一个月内通话300分钟，应选择哪种合算？

查看试题解析
21. 在学习“乘法公式“时，育红中学七（1）班数学兴趣小组在活动课上进行了这样的操作：作两条互相垂直的线段 $A B$ 和 $C D$ ，把大正方形分成四部分（如图所示）.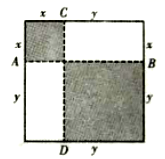

(1)、观察发现
请用两种不同的方法表示图形的面积，得到一个等量关系：

(2)、类比操作
请你作一个图形验证： $(x + y) (2 x + y) = 2 x^{2} + 3 x y + y^{2}$ .

(3)、延伸运用
若 $A B + C D = 14$ ，如图中阴影部分的面积和为13，求 $x y$ 的值.

查看试题解析
22. 如图①，在△ABC中，∠ABC与∠ACB的平分线相交于点P．

(1)、如果∠A＝80°，求∠BPC的度数；

(2)、如图②，作△ABC外角∠MBC，∠NCB的角平分线交于点Q，试探索∠Q、∠A之间的数量关系．

(3)、如图③，延长线段BP、QC交于点E，△BQE中存在一个内角等于另一个内角的2倍，求∠A的度数．

查看试题解析

放水时间（分）	1	2	3	4	…
水池中水量（m³）	48	46	44	42	…