广东省深圳市宝安区2020-2021学年七年级下学期期中数学试题

试卷更新日期：2022-03-15 类型：期中考试

进入出卷网下载

一、单选题

1. 计算（﹣a³）²结果正确的是（）

A、a⁵ B、﹣a⁵ C、﹣a⁶ D、a⁶

查看试题解析
2. 肥皂泡的泡壁厚度大约是0.00000071米，数字0.00000071用科学记数法表示为（）

A、 $7.1 \times 10^{7}$ B、 $0.71 \times 10^{- 6}$ C、 $7.1 \times 10^{- 7}$ D、 $71 \times 10^{- 8}$

查看试题解析
3. 如图，直线c与直线a相交于点A ，与直线b相交于点B ， ∠1＝130°，∠2＝60°，若要使直线a $//$ b ，则将直线a绕点A按如图所示的方向至少旋转（　　）

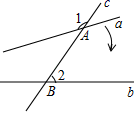A、10° B、20° C、60° D、130°

查看试题解析
4. 如图，△ABC≌△DEF，已知BC＝5cm，BF＝7cm，则EC长为（）

A、1cm B、2cm C、3cm D、4cm

查看试题解析
5. 下列计算正确的是（）

A、x⁵-x³=x² B、3x²y÷3xy=x C、（m²n）³=m⁵n³ D、（x+2）²=x²+4

查看试题解析
6. 如图，将一副三角尺按如图所示方式摆放，EF//AD，∠CAB=∠EDF=90°，∠C=45°，∠EFD=30°，∠BFD的度数是（）

A、15° B、20° C、30° D、45°

查看试题解析
7. 若 $a = 4 + \frac{1}{a}$ ，则 $a^{2} + \frac{1}{a^{2}}$ 的值为（）

A、14 B、16 C、18 D、20

查看试题解析
8. 如图，阴影部分是边长为 $a$ 的大正方形中剪去一个边长为 $b$ 的小正方形后所得到的图形，将阴影部分通过割、拼，形成新的图形，根据这两个图形的面积关系，下列式子正确的是（）

A、 $(a + b) (a - b) = a^{2} - b^{2}$ B、 ${(a + b)}^{2} = a^{2} + a b + b^{2}$ C、 ${(a - b)}^{2} = a^{2} - 2 a b + b^{2}$ D、 $a^{2} - b^{2} = {(a - b)}^{2}$

查看试题解析
9. 如图，在△ABC中，已知点D，E，F分别为边AC，BD，CE的中点，且阴影部分图形面积等于4平方厘米，则△ABC的面积为（）平方厘米

A、8 B、12 C、16 D、18

查看试题解析
10. 如图所示，在Rt△ABC中，AB=AC，D、E是斜边BC上的两点，且∠DAE=45°，△ADC≌△AFB，连接EF，有下列结论∶①BE=DC；②∠BAF=∠DAC； ③∠FAE=45°；④BF⊥BC．其中正确的有（）

A、①②③④ B、②③ C、②③④ D、③④

查看试题解析

二、填空题

11. 若（x- $\frac{1}{2}$ ）²展开后等于x² +ax+ $\frac{1}{4}$ 则a的值为．

查看试题解析
12. 若长方形的周长为24cm，一边为 $x c m$ ，面积为 $y c m^{2}$ ，则 $y$ 与 $x$ 的关系式为 $y =$ ．

查看试题解析
13. 已知2^a=5，2^b=10，2^c=50，那么a、b、c之间满足的等量关系是．

查看试题解析
14. 如图，四边形ABCD的长条形纸带，AB//CD，将长方形沿 EF折叠，A、D分别于A’、D'对应，若 ∠CFE =2∠CFD'，则∠AEF 的度数是．

查看试题解析
15. 如图，△PAB与△PCD均为等腰直角三角形，点C在PB上，若△ABC与△BCD的面积之和为10，则△PAB与△PCD的面积之差为.

查看试题解析

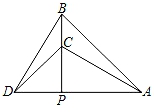
三、解答题

16. 计算∶ -3² ÷（-2）²-|-1 $\frac{1}{3}$ |×6+（-2）³

查看试题解析
17. 先化简，再求值：[（x+2y）²﹣（x+y）（x﹣y）﹣5y²]÷（﹣2x），其中x、y满足|x﹣2y|+（x+2）²＝0．

查看试题解析
18. 完成下面推理过程，在括号内的横线上填空或填上推理依据．
如图，已知∶ AB// EF，EP⊥EQ，∠EQC+∠APE=90°，求证∶ AB//CD
证明： $∵$ AB// EF
$∴$ ∠APE=                  ▲                   （                  ▲                  ）
$∵$ EP⊥EQ
$∴$ ∠PEQ=                  ▲                  （垂直定义）即 ∠QEF+∠PEF = 90°
$∴$ ∠APE+∠QEF=90°
∵·∠EQC+∠APE=90°
$∴$ ∠EQC=                  ▲
$∴$ EF//                  ▲                  （                  ▲                  ）
$∴$ AB// CD（                  ▲                  ）

查看试题解析
19. 如图，已知△ABC中，点P在 BC上．

(1)、试用直尺和圆规在线段AC上找一点D，使∠CPD=∠BAP．（不写作法，但需保留作图痕迹）；

(2)、在（1）的条件下若PD平分∠APC，求证∶∠BAP=∠PBA．

查看试题解析
20. 甲、乙两人从少年宫出发，沿相同的路线分别以不同的速度匀速跑向体育馆，甲先跑一段路程后，乙开始出发，当乙超出甲 150 米时，乙停在原地等候甲，两人相遇后乙又继续以原来的速度跑向体育馆．如图所示是甲、乙两人在跑步的全过程中经过的路程 y（米）与甲出发的时间 x（秒）之间关系的图象．

(1)、在跑步的全过程中，甲一共跑了米，甲的速度为米/秒．

(2)、求图中标注的 a 的值及乙跑步的速度．

(3)、乙在途中等候了多少时间?

查看试题解析
21. 如图所示，已知△ABD≌△CFD，AD⊥BC于D．

(1)、求证∶ CE⊥AB

(2)、已知BC=7，AD=5，求 AF的长．

查看试题解析
22. 如图1，已知两条直线AB，CD被直线EF所截，分别交于点E，点F，EM 平分∠AEF交CD于点M，且∠FEM =∠FME ．

(1)、若2∠AEF = ∠MFE，求∠AEF的度数．

(2)、如图2，点G是射线 MD 上一动点（不与点M，F重合），EH平分∠FEG交CD于点H，过点H作HN ⊥EM 于点N，设∠EHN =α，∠EGF = β．
①当点G在点F的右侧时，若β= 50°，求α的度数；
②当点G 在运动过程中，α 和β之间有怎样的数量关系？请写出你的猜想，并加以证明．

查看试题解析