广东省梅州市五华县2020-2021学年七年级下学期期中数学试题
试卷更新日期:2022-03-15 类型:期中考试
一、单选题
-
1. 下列计算正确的是( )A、 B、 C、 D、2. 某种病毒的直径达0.0000002,由于它的块头较大,难以附着在空气中的粉尘上,因此不会通过空气传播.0.0000002用科学记数法表示为( )A、 B、 C、 D、3. 如下图,在“”字型图中,、被所截,则与是( )
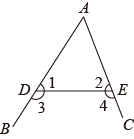 A、同位角 B、内错角 C、同旁内角 D、邻补角4. 已知 , ,那么 的计算结果是( )A、600 B、625 C、675 D、6955. 下列各式中,不能运用平方差公式计算的是( )A、 B、 C、 D、6. 变量与的关系式是 , 当自变量时,因变量的值是( )A、 B、5 C、1 D、7. 如图,下列判断不正确的是( )
A、同位角 B、内错角 C、同旁内角 D、邻补角4. 已知 , ,那么 的计算结果是( )A、600 B、625 C、675 D、6955. 下列各式中,不能运用平方差公式计算的是( )A、 B、 C、 D、6. 变量与的关系式是 , 当自变量时,因变量的值是( )A、 B、5 C、1 D、7. 如图,下列判断不正确的是( ) A、因为 , 所以 B、因为 , 所以 C、因为 , 所以 D、因为 , 所以8. 如下图,将一块含有30°角的直角三角板的两个顶点放在长方形直尺的一组对边上如果 , 那么的度数为( )
A、因为 , 所以 B、因为 , 所以 C、因为 , 所以 D、因为 , 所以8. 如下图,将一块含有30°角的直角三角板的两个顶点放在长方形直尺的一组对边上如果 , 那么的度数为( ) A、40° B、60° C、100° D、70°9. 若能写成一个多项式的平方形式,则的值为( )A、 B、14 C、 D、710. 小明观看了《中国诗词大会》第三期,主题为“人生自有诗意”,受此启发根据邻居家的故事写了一首小诗:“儿子学成今日返,老父早早到车站,儿子到后细端详,父子高兴把家还”,如图用y轴表示父亲与儿子行进中离家的距离,用x轴表示父亲离家的时间,那么下面图象与上述诗的含义大致相吻合的是( )A、
A、40° B、60° C、100° D、70°9. 若能写成一个多项式的平方形式,则的值为( )A、 B、14 C、 D、710. 小明观看了《中国诗词大会》第三期,主题为“人生自有诗意”,受此启发根据邻居家的故事写了一首小诗:“儿子学成今日返,老父早早到车站,儿子到后细端详,父子高兴把家还”,如图用y轴表示父亲与儿子行进中离家的距离,用x轴表示父亲离家的时间,那么下面图象与上述诗的含义大致相吻合的是( )A、 B、
B、 C、
C、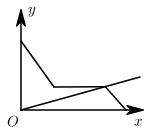 D、
D、
二、填空题
-
11. 一个角的余角比这个角少10°,则这个角为度.12. 如下图,想在河堤两岸搭建一座桥,图中搭建方式中,最短的是 , 理由是 .
 13. 计算: .14. 若 , , 则 .15. 若 , 则的值为 .16. 如下图,C岛在A岛的北偏东65°方向,在B岛的北偏西35°方向,则度.
13. 计算: .14. 若 , , 则 .15. 若 , 则的值为 .16. 如下图,C岛在A岛的北偏东65°方向,在B岛的北偏西35°方向,则度. 17. 如图,一个装有进水管和出水管的容器,从某时刻开始的4分钟内只进水不出水,在随后的8分钟内既进水又出水,接着关闭进水管直到容器内的水放完.假设每分钟的进水量和出水量是两个常数,容器内的水量y(单位:升)与时间x(单位:分)之间的部分关系.那么,从关闭进水管起分钟该容器内的水恰好放完.
17. 如图,一个装有进水管和出水管的容器,从某时刻开始的4分钟内只进水不出水,在随后的8分钟内既进水又出水,接着关闭进水管直到容器内的水放完.假设每分钟的进水量和出水量是两个常数,容器内的水量y(单位:升)与时间x(单位:分)之间的部分关系.那么,从关闭进水管起分钟该容器内的水恰好放完.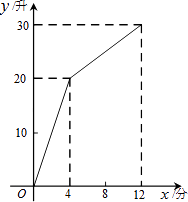
三、解答题
-
18. 计算:(1)、;(2)、 .19. 先化简,再求值: , 其中 , .20. 尺规作图(不写作法,只保留作图痕迹,写出结论)
已知:直线AB,点P在直线AB外.
 (1)、求作:直线CD,使直线CD经过点P,并且CD∥AB;(2)、说明所作图形CD∥AB的理由.21. 某洗衣机在洗涤衣服时,经历了进水、清洗、排水、脱水四个连续过程,其中进水、清洗、排水时洗衣机中的水量(升)与时间(分钟)之间的关系如折线图所示.
(1)、求作:直线CD,使直线CD经过点P,并且CD∥AB;(2)、说明所作图形CD∥AB的理由.21. 某洗衣机在洗涤衣服时,经历了进水、清洗、排水、脱水四个连续过程,其中进水、清洗、排水时洗衣机中的水量(升)与时间(分钟)之间的关系如折线图所示.
根据图象解答下列问题:
(1)、洗衣机的进水时间是多少分钟?清洗时洗衣机中的水量是多少升?(2)、已知洗衣机的排水速度为每分钟19升,①求排水时y与x之间的关系式.
②如果排水时间为2分钟,求排水结束时洗衣机中剩下的水量.
22. 请认真观察图形,解答下列问题: (1)、根据图中条件,试用两种不同方法表示两个阴影图形的面积的和.
(1)、根据图中条件,试用两种不同方法表示两个阴影图形的面积的和.方法1:;
方法2: .
(2)、从中你能发现什么结论,请用等式表示出来: ;(3)、利用(2)中结论解决下面的问题:若 , , 求的值.23. 如图,已知: , 垂足为点 , , 垂足为点 , 点在上,连接 . (1)、与平行吗?为什么?(2)、若、 , 求的度数.24. 从边长为的正方形剪掉一个边长为的正方形(如图1),然后将剩余部分拼成一个长方形(如图2).
(1)、与平行吗?为什么?(2)、若、 , 求的度数.24. 从边长为的正方形剪掉一个边长为的正方形(如图1),然后将剩余部分拼成一个长方形(如图2). (1)、上述操作能验证的等式是____(请选择正确的一个).A、 B、 C、(2)、若 , , 求的值;(3)、计算: .25. 如图1, , , . 求的度数.小明的思路是:过作 , 通过平行线的性质来求 .
(1)、上述操作能验证的等式是____(请选择正确的一个).A、 B、 C、(2)、若 , , 求的值;(3)、计算: .25. 如图1, , , . 求的度数.小明的思路是:过作 , 通过平行线的性质来求 . (1)、按小明的思路,易求得的度数为度;(2)、问题迁移:如图2, , 点在射线上运动,记 , , 当点在、两点之间运动时,问与、之间有何数量关系?请说明理由;(3)、在(2)的条件下,如果点在、两点外侧运动时(点与点、、三点不重合),请直接写出与、之间的数量关系.
(1)、按小明的思路,易求得的度数为度;(2)、问题迁移:如图2, , 点在射线上运动,记 , , 当点在、两点之间运动时,问与、之间有何数量关系?请说明理由;(3)、在(2)的条件下,如果点在、两点外侧运动时(点与点、、三点不重合),请直接写出与、之间的数量关系.