广东省广州市海珠区2020-2021学年七年级下学期期中数学试题

试卷更新日期：2022-03-15 类型：期中考试

进入出卷网下载

一、单选题

1. 下面四个图形中， $∠ 1$ 与 $∠ 2$ 是对顶角的是（）

A、 B、 C、 D、

查看试题解析
2. 在平面直角坐标系中，点A（2，-3）在第（）象限.

A、一 B、二 C、三 D、四

查看试题解析
3. 已知 ${\begin{matrix} x = 2 \\ y = 1 \end{matrix}$ 是方程 $k x - y = 3$ 的解，那么 $k$ 的值是（）

A、1 B、－1 C、－2 D、2

查看试题解析
4. 下列计算正确的是（）

A、 $\sqrt{9} = \pm 3$ B、 $- \sqrt{9} = - 3$ C、|﹣3|＝﹣3 D、﹣3²＝9

查看试题解析
5. 如图，下列条件中，能判定a∥b的是（）

A、∠1=∠2 B、∠1=∠4 C、∠1+∠3=180° D、∠3+∠4=180°

查看试题解析
6. 以下四个命题：
①如果 $a < 0 ， b < 0$ ，那么 $a b < 0$ ；②两个负数比较大小，绝对值大的反而小；③同角的余角相等；④如果两条直线被第三条直线所截，那么内错角相等.其中属于真命题的是（）

A、①② B、①③ C、②③ D、②④

查看试题解析
7. 在平面直角坐标系中，一个长方形的三个顶点的坐标分别为 $(- 3 ， - 2) ， (- 3 ， 1) ， (2 ， - 2) ，$ 则第四个顶点的坐标为（）

A、 $(2 ， 1)$ B、 $(2 ， 2)$ C、 $(3 ， 1)$ D、 $(2 ， - 5)$

查看试题解析
8. 方程组 ${\begin{cases} 3 x - y = a + 2 \\ x + 5 y = a \end{cases} \begin{array}{l} \end{array}$ 的解 $x$ ， $y$ 满足 $x$ 是 $y$ 的2倍，则a的值为（）

A、－7 B、－11 C、－3 D、－2.2

查看试题解析
9. 有一个数值转换器，原理如下：当输入的x＝81时，输出的y等于（）

A、2 B、3 C、 $\sqrt{3}$ D、 $\sqrt{2}$

查看试题解析
10. 如图所示，在平面直角坐标系中，已知A的坐标为（2，2），B的坐标为（3，3），点C的横、纵坐标都是不少于0且不超过4的整数，且以A ， B ， C为顶点的三角形面积为1，则点C的个数为（）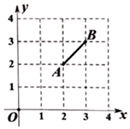

A、3个 B、4个 C、5个 D、6个

查看试题解析

二、填空题

11. 点A（3，﹣2）到x轴的距离是．

查看试题解析
12. 如果 $| x - 8 | + (y - 2)^{2} = 0$ ，则 $\sqrt{x y} =$

查看试题解析
13. 在△ABC中，∠ACB＝90°，CD⊥AB于点D，则线段ACAD（填＞、＜、＝）．

查看试题解析
14. 已知方程组 ${\begin{array}{l} 2 x + 3 y = 12 \\ 3 x + 2 y = 18 \end{array}$ ，则x+y的值为．

查看试题解析
15. 夏季荷花盛开，为了便于游客领略“人从桥上过，如在河中行”的美好意境，某景点拟在如图所示的长方形荷塘上架设小桥．若荷塘周长为800m，且桥宽忽略不计，则小桥的总长为m.

查看试题解析
16. 对于实数p，我们规定：用＜p＞表示不小于p的最小整数，例如：＜4＞＝4，＜ $\sqrt{3}$ ＞＝2．现对72进行如下操作：
即对72只需进行3次操作后变为2，类似地只需进行3次操作后变为2的所有正整数中，最大的是．

查看试题解析

三、解答题

17.

(1)、计算 $\sqrt{0.04} + \sqrt[3]{- 27} + \sqrt{(- 2)^{2}}$ ；

(2)、求 $x$ 的值： $(x - 1)^{2} = 25$ ．

查看试题解析
18. 解方程组：

(1)、 ${\begin{array}{l} x - y = 3 \\ x - 3 y = - 1 \end{array}$ ；

(2)、 ${\begin{array}{l} 2 x + 3 y = 16 \\ 3 x - 2 y = 11 \end{array}$ ．

查看试题解析
19. 如图所示，∠1＝∠2，∠3＝75°，求∠4的度数．

查看试题解析
20. 在下列网格中建立平面直角坐标系如图，每个小正方形的边长均为1个单位长度，已知 $A (1 ， 1)$ 、 $B (3 ， 4)$ 和 $C (4 ， 2)$ .

(1)、在图中标出点 $A$ 、 $B$ 、 $C$ .

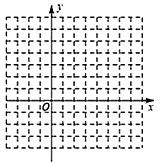(2)、将点 $C$ 向下平移3个单位到 $D$ 点，将点 $A$ 先向左平移3个单位，再向下平移1个单位到E点，在图中标出 $D$ 点和 $E$ 点.

(3)、求 $Δ E B D$ 的面积 $S_{Δ E B D}$ .

查看试题解析
21. 已知2a﹣1的算术平方根是3，b﹣1是 $\sqrt{5}$ 的整数部分，c+1和9的平方根相等，求a﹣2b﹣c的值.

查看试题解析
22. 如图，直线AB，CD相交于点O，OE平分∠AOC，OF⊥CD于点O．

(1)、若∠BOF＝68°30′，求∠AOE的度数；

(2)、若∠AOD：∠AOE＝1：4，求∠BOF的度数．

查看试题解析
23. 张华想用一块面积为400cm²的正方形纸片，沿着边的方向剪出一块面积为300cm²的长方形纸片，使它的长宽之比为3：2.他不知能否裁得出来，正在发愁.李明见了说：“别发愁，一定能用一块面积大的纸片裁出一块面积小的纸片.”你同意李明的说法吗？张华能用这块纸片裁出符合要求的纸片吗？

查看试题解析
24. 如图，以直角三角形AOC的直角顶点O为原点，以OC、OA所在直线为x轴和y轴建立平面直角坐标系，点A（0，a），C（b，0）满足 $\sqrt{a - 2 b}$ +|b﹣2|＝0，D为线段AC的中点．在平面直角坐标系中，以任意两点P（x₁ ， y₁）、Q（x₂ ， y₂）为端点的线段中点坐标为（ $\frac{x_{1} + x_{2}}{2}$ ， $\frac{y_{1} + y_{2}}{2}$ ）．

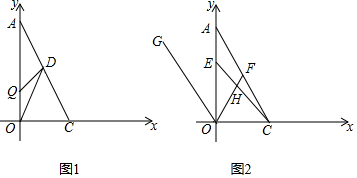(1)、则A点的坐标为；点C的坐标为， D点的坐标为．

(2)、已知坐标轴上有两动点P、Q同时出发，P点从C点出发沿x轴负方向以1个单位长度每秒的速度匀速移动，Q点从O点出发以2个单位长度每秒的速度沿y轴正方向移动，点Q到达A点整个运动随之结束．设运动时间为t（t＞0）秒．问：是否存在这样的t，使S_△ODP＝S_△ODQ，若存在，请求出t的值；若不存在，请说明理由．

(3)、点F是线段AC上一点，满足∠FOC＝∠FCO，点G是第二象限中一点，连OG，使得∠AOG＝∠AOF．点E是线段OA上一动点，连CE交OF于点H，当点E在线段OA上运动的过程中，请确定∠OHC，∠ACE和∠OEC的数量关系，并说明理由．

查看试题解析
25. 如图1，AD∥BC，∠BAD的平分线交BC于点G，∠BCD＝90°．

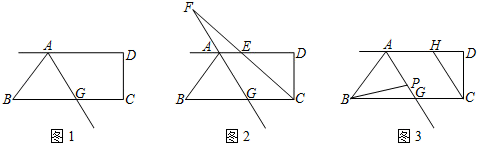(1)、求证：∠BAG＝∠BGA；

(2)、如图2，若∠ABG＝50°，∠BCD的平分线交AD于点E、交射线GA于点F．求∠AFC的度数；

(3)、如图3，线段AG上有一点P，满足∠ABP＝3∠PBG，过点C作CH∥AG．若在直线AG上取一点M，使∠PBM＝∠DCH，请直接写出 $\frac{∠ ABM}{∠ GBM}$ 的值．

查看试题解析