广东省佛山市南海区2020-2021学年七年级下学期期中数学试题
试卷更新日期:2022-03-15 类型:期中考试
一、单选题
-
1. 以下各组长度的线段为边,能构成三角形的是( )A、8cm、5cm、3cm B、6cm、8cm、15cm C、8cm、4cm、3cm D、4cm、6cm、5cm2. 下列计算正确的是( )A、( B、; C、( D、.3. 据中新社北京2010年12月8日电,2010年中国粮食总产量达到546 400 000吨,用科学记数法表示为( )A、5.464×107吨 B、5.464×108吨 C、5.464×109吨 D、5.464×1010吨4. 如图,工人师傅砌门时,常用一根木条EF来固定长方形门框ABCD,使其不变形,这样做的根据是( )
 A、两点之间线段最短 B、长方形的四个角都是直角 C、长方形是轴对称图形 D、三角形具有稳定性5. 如图所示,向放在水槽底部的烧杯注水(流量一定,住满烧杯后,继续注水,直至住满水槽). 水槽中水面上升高度h与注水时间t之间的关系大致是( )
A、两点之间线段最短 B、长方形的四个角都是直角 C、长方形是轴对称图形 D、三角形具有稳定性5. 如图所示,向放在水槽底部的烧杯注水(流量一定,住满烧杯后,继续注水,直至住满水槽). 水槽中水面上升高度h与注水时间t之间的关系大致是( ) A、
A、 B、
B、 C、
C、 D、
D、 6. 如图所示, , 可以判断线段平行的是( )
6. 如图所示, , 可以判断线段平行的是( ) A、BDEC B、BCDE C、DFAC D、ABEF7. 计算:的结果是( )A、 B、 C、 D、8. 一辆汽车和一辆摩托车分别从A、B两地去同一城市,它们离A地的距离随时间变化的图象如图所示.则下列结论不正确的是( )
A、BDEC B、BCDE C、DFAC D、ABEF7. 计算:的结果是( )A、 B、 C、 D、8. 一辆汽车和一辆摩托车分别从A、B两地去同一城市,它们离A地的距离随时间变化的图象如图所示.则下列结论不正确的是( ) A、摩托车比汽车晚到1 h B、A、B两地的距离为20 km C、摩托车的速度为45 km/h D、汽车的速度为60 km/h9. 如图, , 再添加一个条件,不能判定的是( )
A、摩托车比汽车晚到1 h B、A、B两地的距离为20 km C、摩托车的速度为45 km/h D、汽车的速度为60 km/h9. 如图, , 再添加一个条件,不能判定的是( ) A、 B、 C、 D、10. 用四个全等的矩形和一个小正方形拼成如图所示的大正方形,已知大正方形的面积是169,小正方形的面积是9,若用x,y表示矩形的长和宽(),则下列关系式中不正确的是( )
A、 B、 C、 D、10. 用四个全等的矩形和一个小正方形拼成如图所示的大正方形,已知大正方形的面积是169,小正方形的面积是9,若用x,y表示矩形的长和宽(),则下列关系式中不正确的是( )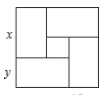 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
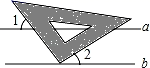
11. 如图,小明课间把老师的三角板的直角顶点放在黑板的两条平行线a、b上,已知∠1=55°,则∠2的度数为 .
 12. 一个长方体文具盒,长、宽、高如图所示(单位:cm),该文具盒的体积是 .
12. 一个长方体文具盒,长、宽、高如图所示(单位:cm),该文具盒的体积是 . 13. 若 , 则m的值为 .14. 一个角的度数是40°,那么它的余角的度数是 .15. 等腰直角三角形顶点的度数y是随着底角的度数x的变化而变化的,则y与x的关系式是 .16. 如图,把一个长方形纸片沿EF折叠后,点D , C分别落在 , 的位置 若 ,则 的度数为 .
13. 若 , 则m的值为 .14. 一个角的度数是40°,那么它的余角的度数是 .15. 等腰直角三角形顶点的度数y是随着底角的度数x的变化而变化的,则y与x的关系式是 .16. 如图,把一个长方形纸片沿EF折叠后,点D , C分别落在 , 的位置 若 ,则 的度数为 .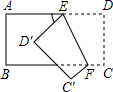 17. 请先观察下列等式,再填空: , , , , …,通过观察归纳,写出第n个等式是:(n为正整数)
17. 请先观察下列等式,再填空: , , , , …,通过观察归纳,写出第n个等式是:(n为正整数)三、解答题
-
18. 计算: .19. 先化简,再求值:
,其中 ,
20. 尺规作图:如图,光纤CO照射到镜面AB上的O点,反射光线与镜面AB的夹角等于 , 请作出CO经过镜面反射后的光线. 21. 弹簧挂上物体后会伸长,已知一弹簧的长度(cm)与所挂物体的质量(kg)之间的关系如表:(弹簧最大承重20kg)
21. 弹簧挂上物体后会伸长,已知一弹簧的长度(cm)与所挂物体的质量(kg)之间的关系如表:(弹簧最大承重20kg)所挂物体质量x
0
1
2
3
4
5
6
弹簧长度y
12
12.5
13
13.5
14
14.5
15
(1)、如表反映的变化过程中,自变量、因变量分别是什么?(2)、当物体的质量为2kg时,弹簧的长度是多少?(3)、如果物理的质量为xkg,弹簧长度为ycm,请根据如表写出y与x之间的关系式;(4)、当弹簧的长度为15.5cm时,根据(3)的关系式,求出物体的质量.22. 如图,已知DF∥AB,且 .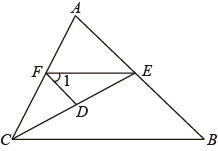 (1)、求证:EF∥BC;(2)、若CE平分 , 且 , 求的度数.23. 已知△ABN和△ACM位置如图所示,AB=AC,AD=AE,∠1=∠2.
(1)、求证:EF∥BC;(2)、若CE平分 , 且 , 求的度数.23. 已知△ABN和△ACM位置如图所示,AB=AC,AD=AE,∠1=∠2.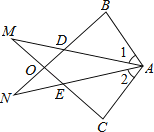 (1)、求证:BD=CE;(2)、求证:∠M=∠N.24. 两个边长分别为a和b的正方形如图放置(图1),其未叠合部分(阴影)面积为;若图1中大正方形的右下角摆放一个边长为b的小正方形(如图2),两个小正方形叠合部分(阴影)面积为 .
(1)、求证:BD=CE;(2)、求证:∠M=∠N.24. 两个边长分别为a和b的正方形如图放置(图1),其未叠合部分(阴影)面积为;若图1中大正方形的右下角摆放一个边长为b的小正方形(如图2),两个小正方形叠合部分(阴影)面积为 .

 (1)、用含a、b的代数式分别表示、;(2)、若 , , 求的值;(3)、当时,求阴影部分的值.25. 如图1,把一块直角三角尺ABC的直角顶点C放置在水平直线MN上,在中, , , 试回答下列问题:
(1)、用含a、b的代数式分别表示、;(2)、若 , , 求的值;(3)、当时,求阴影部分的值.25. 如图1,把一块直角三角尺ABC的直角顶点C放置在水平直线MN上,在中, , , 试回答下列问题: (1)、若把三角尺ABC绕着点C按顺时针方向旋转,当AB∥MN时,度;(2)、在三角尺ABC绕着点C按顺时针方向旋转过程中,分别作AM⊥MN于M,BN⊥MN与N,若 , , 求MN.(3)、三角尺ABC绕着点C按顺时针方向继续旋转到图3的位置,其他条件不变,则AM、BN与MN之间有什么关系?请说明理由.
(1)、若把三角尺ABC绕着点C按顺时针方向旋转,当AB∥MN时,度;(2)、在三角尺ABC绕着点C按顺时针方向旋转过程中,分别作AM⊥MN于M,BN⊥MN与N,若 , , 求MN.(3)、三角尺ABC绕着点C按顺时针方向继续旋转到图3的位置,其他条件不变,则AM、BN与MN之间有什么关系?请说明理由.