安徽省芜湖市无为市2020-2021学年七年级下学期期中数学试题

试卷更新日期：2022-03-15 类型：期中考试

进入出卷网下载

一、单选题

1. 已知一个数的立方根是﹣ $\frac{1}{2}$ ，则这个数是（）

A、﹣ $\frac{1}{8}$ B、 $\frac{1}{8}$ C、 $\frac{1}{4}$ D、﹣ $\frac{3}{2}$

查看试题解析
2. 在平面直角坐标系中，点A（1，﹣2021）在（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
3. 如图，∠C的内错角是（）

A、∠1 B、∠3 C、∠2 D、∠4

查看试题解析
4. 在平面直角坐标系中，点P（﹣3，﹣4）到y轴的距离为（）

A、﹣3 B、﹣4 C、3 D、4

查看试题解析
5. 计算 $\sqrt{4}$ ﹣ $\sqrt[3]{- 27}$ ﹣ $\sqrt{81}$ 的结果为（）

A、4 B、﹣4 C、10 D、﹣10

查看试题解析
6. 如图，直线AB∥CD，AE平分∠CAB交CD于点E，若∠C=52°，则∠AED的度数为（）

A、104° B、118° C、116° D、128°

查看试题解析
7. 已知a是绝对值最小的数，b是最大的负整数，c与d互为相反数，e是 $\sqrt{6}$ ，则式子 $\sqrt{a}$ ﹣|﹣b﹣e|＋|c＋d|×2021的值为（）

A、1﹣ $\sqrt{6}$ B、 $\sqrt{6}$ ﹣1 C、﹣ $\sqrt{6}$ D、2﹣ $\sqrt{6}$

查看试题解析
8. 物体自由下落时，下落距离h（单位：米）可用公式 $h = 5 t^{2}$ 来估算，其中t（t＞0单位：秒）表示物体下落的时间．若一个篮球掉入80米深的山谷中，落入谷底前不与其他物体接触，则该篮球掉落到谷底需要的时间为（）

A、2秒 B、4秒 C、16秒 D、20秒

查看试题解析
9. 如图，直线AB∥CD∥EF，点O在直线EF上，下列结论正确的是（）

A、∠ $α$ ＋∠ $β$ ﹣∠ $γ$ ＝90° B、∠ $α$ ＋∠ $β$ ＋∠ $γ$ ＝180° C、∠ $γ$ ＋∠ $β$ ﹣∠ $α$ ＝180° D、∠ $α$ ＋∠ $γ$ ﹣∠ $β$ ＝180°

查看试题解析
10. 如图，小球起始时位于（3，0）处，沿所示的方向击球，小球运动的轨迹如图所示．如果小球起始时位于（1，0）处，仍按原来方向击球，小球第一次碰到球桌边时，小球的位置是（0，1），那么小球第2021次碰到球桌边时，小球的位置是（）

A、（3，4） B、（5，4） C、（7，0） D、（8，1）

查看试题解析

二、填空题

11. 若小明坐在教室的6列7行，记为（6，7），则小华坐在同一教室的5列3行，应记为．

查看试题解析
12. 如图，直线a∥b，直角三角形的直角顶点在直线b上，已知∠1=48°，则∠2的度数是度．

查看试题解析
13. 有一个数值转换器，原理如图所示，当输入x的值为36时，输出的y的值为．

查看试题解析
14. 如图，AO∥CD，OB∥DE，∠O=40°，

(1)、∠D的度数为．

(2)、在平面内取一点M，作射线MP∥OA，MQ∥OB，则∠PMQ的度数为．

查看试题解析

三、解答题

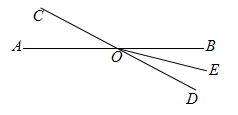
15. 如图，直线AB，CD相交于点O，OE平分∠BOD，若∠BOE=20°，求∠AOC的度数．

查看试题解析
16. 把下列各数填在相应的横线上
1.6，2021，﹣ $\sqrt{2}$ ， $- \frac{3}{2}$ ， 0. $\dot{3} \dot{1}$ ， $\sqrt{3}$ ， 0， $\sqrt[3]{8}$ ， 1.303003003…（每相邻两个3之间的0的个数依次加1）

(1)、整数：．

(2)、分数：．

(3)、无理数：．

查看试题解析
17. 如图，AB，CD相交于点E，∠ACE=∠AEC，∠BDE=∠BED，过A作AF⊥BD，垂足为F．求证：AC⊥AF．

查看试题解析
18. 已知某个正数的两个平方根分别是a﹣19和 $\frac{a + 1}{3}$ ， b﹣22的立方根是4．

(1)、求b﹣a的值．

(2)、求a+b的平方根．

查看试题解析
19. 如图所示的是某学校的平面示意图，已知旗杆的位置是（﹣1，2），实验室的位置是（2，3）．

(1)、根据所给条件建立适当的平面直角坐标系，并用坐标表示食堂、宿舍楼和大门的位置．

(2)、已知办公楼的位置是（﹣2，1），教学楼的位置是（3，1），在（1）中所画的图中标出办公楼和教学楼的位置．

查看试题解析
20. 在平面直角坐标系中，有A（﹣2，a＋2），B（a﹣1，4），C（b﹣3，b＋1）三点．

(1)、当点C在y轴上时，求点C的坐标．

(2)、当AB∥x轴时，求A，B两点间的距离．

(3)、当CD⊥x轴于点D，且CD＝2时，求点C的坐标．

查看试题解析
21. 如图，三角形A′B′C′是由三角形ABC经过某种平移得到的，点A与点A′，点C与点C′分别对应，且这六个点都在格点（小正方形的顶点）上，解答下列问题：

(1)、分别写出点A和点A′的坐标，并说明三角形A′B′C′是由三角形ABC经过怎样的平移得到的．

(2)、连接BC′，∠CBC′与∠B′C′O之间的数量关系为．

(3)、若M（a﹣2，2b﹣3）是三角形ABC内一点，它随三角形ABC按（1）（2a﹣7，9﹣b），分别求a和b的值．

(4)、三角形A′B′C′的面积为．

查看试题解析
22. 操作探究：已知在纸面上有一数轴如图所示．

(1)、折叠纸面，使1表示的点与﹣1表示的点重合，则﹣ $\sqrt{2}$ 表示的点重合．

(2)、折叠纸面，使﹣1表示的点与3表示的点重合，回答以下问题：
①2表示的点与表示的点重合；
② $\sqrt{5}$ ＋1表示的点与表示的点重合．

(3)、已知在数轴上点A表示的数是a，点A移动4个单位，此时点A表示的数和a是互为相反数，求a的值．

查看试题解析
23. 三角形ABC中，D是AB上一点，DE∥BC交AC于点E，点F是线段DE延长线上一点，连接FC，∠BCF+∠ADE=180°．

(1)、如图1，求证：CF∥AB；

(2)、如图2，连接BE，若∠ABE=40°，∠ACF=60°，
①求∠BEC的度数；
②如图2，点G是线段FC延长线上一点，若∠EBC：∠ECB=7：13，BE平分∠ABG，求∠CBG的度数．

查看试题解析