安徽省铜陵市铜官区2020-2021学年七年级下学期期中数学试题
试卷更新日期:2022-03-15 类型:期中考试
一、单选题
-
1. 下列说法正确的是( )A、16的立方根是 B、-64没有立方根 C、64的平方根是8 D、的算术平方根是22. 已知点在轴上,则( )A、 B、6 C、 D、13. 点P在y轴左方、x轴上方,距y轴、x轴分别为3、4个单位长度,点P的坐标是( )A、(3,–4) B、(–3,4) C、(4,–3) D、(–4,3)4. 如图,已知AB∥CD∥EF,若∠ABC=α,∠CEF=β,则∠BCE的度数为( )
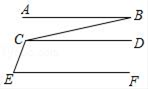 A、α+β B、β﹣α C、180°﹣β+α D、180°﹣α+β5. 下列四个命题①过一点有且只有一条直线与已知直线垂直;②两条直线被第三条直线所截,内错角相等;③一个正实数的算术平方根一定是正实数;④ 是 的平方根,其中真命题的个数为( )A、 B、 C、 D、6. 如图,将矩形ABCD沿GH折叠,点C落在点Q处,点D落在AB边上的点E处,若∠AGE=32°,则∠GHC等于( )
A、α+β B、β﹣α C、180°﹣β+α D、180°﹣α+β5. 下列四个命题①过一点有且只有一条直线与已知直线垂直;②两条直线被第三条直线所截,内错角相等;③一个正实数的算术平方根一定是正实数;④ 是 的平方根,其中真命题的个数为( )A、 B、 C、 D、6. 如图,将矩形ABCD沿GH折叠,点C落在点Q处,点D落在AB边上的点E处,若∠AGE=32°,则∠GHC等于( )
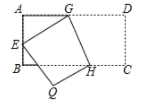 A、112° B、110° C、108° D、106°7. 如图所示,已知 , , , 的度数是( )
A、112° B、110° C、108° D、106°7. 如图所示,已知 , , , 的度数是( )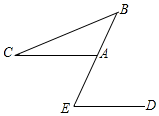 A、 B、 C、 D、8. 在平面直角坐标系中,对于点P(x,y),我们把点P′(-y+1,x+1)叫做点P伴随点.已知点A1的伴随点为A2 , 点A2的伴随点为A3 , 点A4的伴随点为A4 , …,这样依次得到点A1 , A2 , A3 , …,An,….若点A1的坐标为(2,4),点A2021的坐标为( )A、(-3,3) B、(-2,2) C、(3,-1) D、(2,4)9. 估算的运算结果应在( )A、3到4之间 B、4到5之间 C、5到6之间 D、6到7之间10. 如图,在平面直角坐标系xOy中,点P(1,0).点P第1次向上跳动1个单位至点P1(1,1),紧接着第2次向左跳动2个单位至点P2(﹣1,1),第3次向上跳动1个单位至点P3 , 第4次向右跳动3个单位至点P4 , 第5次又向上跳动1个单位至点P5 , 第6次向左跳动4个单位至点P6 , ….照此规律,点P第100次跳动至点P100的坐标是( )
A、 B、 C、 D、8. 在平面直角坐标系中,对于点P(x,y),我们把点P′(-y+1,x+1)叫做点P伴随点.已知点A1的伴随点为A2 , 点A2的伴随点为A3 , 点A4的伴随点为A4 , …,这样依次得到点A1 , A2 , A3 , …,An,….若点A1的坐标为(2,4),点A2021的坐标为( )A、(-3,3) B、(-2,2) C、(3,-1) D、(2,4)9. 估算的运算结果应在( )A、3到4之间 B、4到5之间 C、5到6之间 D、6到7之间10. 如图,在平面直角坐标系xOy中,点P(1,0).点P第1次向上跳动1个单位至点P1(1,1),紧接着第2次向左跳动2个单位至点P2(﹣1,1),第3次向上跳动1个单位至点P3 , 第4次向右跳动3个单位至点P4 , 第5次又向上跳动1个单位至点P5 , 第6次向左跳动4个单位至点P6 , ….照此规律,点P第100次跳动至点P100的坐标是( )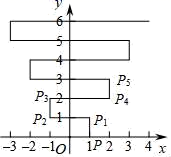 A、(﹣26,50) B、(﹣25,50) C、(26,50) D、(25,50)
A、(﹣26,50) B、(﹣25,50) C、(26,50) D、(25,50)二、填空题
-
11. 已知点到两坐标轴的距离相等则点P的坐标为 .12. 如图,将ABE向右平移后得到△DCF(点B、C、E、F在同一条直线上),如果ABE的周长是12cm,四边形ABFD的周长是18cm,那么平移的距离为cm.
 13. 如图,可以由三角形平移得到的三角形有个.(不包括)
13. 如图,可以由三角形平移得到的三角形有个.(不包括) 14. 观察下面一列数:﹣1,2,﹣3,4,﹣5,6……将这列数排成如图的形式按照上述规律排下去,那么第13行左边第12个数是 .
14. 观察下面一列数:﹣1,2,﹣3,4,﹣5,6……将这列数排成如图的形式按照上述规律排下去,那么第13行左边第12个数是 .
三、解答题
-
15.(1)、计算 ;(2)、已知 , 求的值.16. 已知平面直角坐标系中有一点 .(1)、若点M到x轴的距离为1,请求出点M的坐标.(2)、若点 ,且 轴,请求出点M的坐标.17. 如图,E,G是分别是AB,AC上的点,F,D是BC上的点,连接EF,AD,DG,如果AB∥DG,∠1+∠2=180°.
 (1)、判断AD与EF的位置关系,并说明理由;(2)、若DG是∠ADC的平分线,∠2=145°,求∠B的度数.18. 如图,已知AB∥CD,BE平分∠ABC,DE平分∠ADC,∠BAD=80°,试求:
(1)、判断AD与EF的位置关系,并说明理由;(2)、若DG是∠ADC的平分线,∠2=145°,求∠B的度数.18. 如图,已知AB∥CD,BE平分∠ABC,DE平分∠ADC,∠BAD=80°,试求: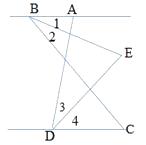 (1)、∠EDC的度数;
(1)、∠EDC的度数;
(2)、若∠BCD=n°,试求∠BED的度数。(用含n的式子表示)19. 如图所示,在长方形中有两条对称的等宽折条和一条长方形的横条,其中 , , , , 求阴影部分面积. 20.(1)、通过计算下列各式的值探究问题:
20.(1)、通过计算下列各式的值探究问题:①=;=;=;= .
探究:对于任意非负有理数a,= .
②=;= ;=;= .
探究:对于任意负有理数a,= .
综上,对于任意有理数a,= .
(2)、应用(1)所得的结论解决问题:有理数a,b在数轴上对应的点的位置如图所示,化简:--+|a+b|. 21. 在直角坐标系中, 的三个顶点的位置如图所示,现将 沿 的方向平移,使得点 移至图中的点 的位置.
21. 在直角坐标系中, 的三个顶点的位置如图所示,现将 沿 的方向平移,使得点 移至图中的点 的位置. (1)、在直角坐标系中,画出平移后所得 (其中 、 分别是 、 的对应点).(2)、(1)中所得的点 , 的坐标分别是 , .(3)、直接写出 的面积为.22. 如图,在长方形 中, 为平面直角坐标系的原点,点 坐标为 ,点 的坐标为 ,且 , 满足 ,点 在第一象限内,点 从原点出发,以每秒2个单位长度的速度沿着 的线路移动.
(1)、在直角坐标系中,画出平移后所得 (其中 、 分别是 、 的对应点).(2)、(1)中所得的点 , 的坐标分别是 , .(3)、直接写出 的面积为.22. 如图,在长方形 中, 为平面直角坐标系的原点,点 坐标为 ,点 的坐标为 ,且 , 满足 ,点 在第一象限内,点 从原点出发,以每秒2个单位长度的速度沿着 的线路移动. (1)、点 的坐标为;(2)、当点 移动4秒时,请指出点 的位置,并求出点 的坐标;(3)、在移动过程中,当点 到 轴的距离为5个单位长度时,求点 移动的时间.23. 如图1,已知两条直线 , 被直线所截,分别交于点 , 点 , 平分交于点 , 且 .
(1)、点 的坐标为;(2)、当点 移动4秒时,请指出点 的位置,并求出点 的坐标;(3)、在移动过程中,当点 到 轴的距离为5个单位长度时,求点 移动的时间.23. 如图1,已知两条直线 , 被直线所截,分别交于点 , 点 , 平分交于点 , 且 .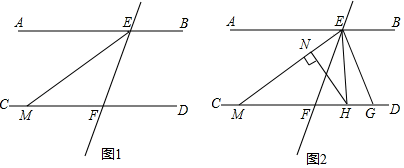 (1)、判断直线与直线是否平行,并说明理由;(2)、如图2,点是射线上一动点(不与点 , 重合),平分交于点 , 过点作于点 , 设 , .
(1)、判断直线与直线是否平行,并说明理由;(2)、如图2,点是射线上一动点(不与点 , 重合),平分交于点 , 过点作于点 , 设 , .①当点在点的右侧时,若 , 求的度数;
②当点在运动过程中,和之间有怎样的数量关系?请写出你的猜想,并加以证明.