安徽省合肥市庐江县2020-2021学年七年级下学期期中数学试题

试卷更新日期：2022-03-15 类型：期中考试

进入出卷网下载

一、单选题

1. 以下图形中，∠1与∠2表示邻补角的是（）

A、 B、 C、 D、

查看试题解析
2. $\sqrt{16}$ 的平方根是（　　）

A、±4 B、4 C、±2 D、2

查看试题解析
3. 已知点P(m，n)，且mn＞0，m+n＜0，则点P在（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
4. 关于 $\sqrt{5}$ ， $\sqrt[3]{7}$ ，2大小比较正确的是（）

A、 $\sqrt[3]{7}$ ＜2＜ $\sqrt{5}$ B、 $\sqrt{5}$ ＜ $\sqrt[3]{7}$ ＜2 C、 $\sqrt[3]{7}$ ＜ $\sqrt{5}$ ＜2 D、2＜ $\sqrt{5}$ ＜ $\sqrt[3]{7}$

查看试题解析
5. 如图，不能判定AB∥CD的条件是（）

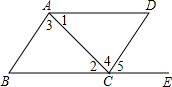A、∠1＝∠2 B、∠B＋∠BCD＝180° C、∠3＝∠4 D、∠B＝∠5

查看试题解析
6. 如图，将 $△$ ABC沿CB向左平移3cm得到 $△$ DEF，AB，DF相交于点G，如果 $△$ ABC的周长是12cm，那么 $△$ ADG与 $△$ GBF周长之和为（）

A、12cm B、15cm C、18cm D、24cm

查看试题解析
7. 命题：①对顶角相等；②同旁内角互补；③如果两条直线垂直于同一条直线，那么这两条直线互相平行；④过一点有且只有一条直线与已知直线平行；⑤平行于同一条直线的两条直线互相平行．其中是真命题的有（）

A、5个 B、4个 C、3个 D、2个

查看试题解析
8. “引江济淮”工程是一项以城乡供水和发展江淮航运为主要目的大型跨流域调水工程．目前该工程经过我县段正紧锣密鼓地进行施工．为了测量村庄A是否对河道施工有影响，需测量村庄A到河道的距离．某测绘队沿河道规划路线MN进行测量，如图，测量角度∠APN与线段AP的长度如表所示：
∠APN度数（°）
52.3
69.3
88.8
93.5
105.8
117.8
AP长度（m）
693
587
549
550
570
620
则下面说法正确的是（）

A、村庄A到河道距离等于549m B、村庄A到河道距离小于549m C、村庄A到河道距离大于549m D、村庄A到河道距离等于550m

查看试题解析
9. 如图，长方形BCDE的各边分别平行于x轴或y轴，物体甲和物体乙分别由点A(4，0)同时出发，沿长方形BCDE的边作环绕运动，物体甲按逆时针方向以2个单位/秒匀速运动，物体乙按顺时针方向以6个单位秒匀速运动，则两个物体运动后的第2021次相遇地点的坐标是（）

A、(0，2) B、(﹣4，0) C、(0，﹣2) D、(4，0)

查看试题解析
10. 如图是庐城一些地点的分布示意图．在图中，分别以向右，向上为x轴，y轴的正方向建立平面直角坐标系，有如下四个结论：
①当表示政府广场的点的坐标为（0，0），表示庐江汽车站的点的坐标为（﹣2，﹣3）时，表示周瑜文化园的点的坐标为（6，﹣4）；
②当表示政府广场的点的坐标为（0，0），表示庐江汽车站的点的坐标为（﹣4，﹣6）时，表示周瑜文化园的点的坐标为（12，﹣8）；
③当表示政府广场的点的坐标为（1，1），表示庐江汽车站的点的坐标为（﹣3，﹣5）时，表示周瑜文化园的点的坐标为（13，﹣7）；
④当表示政府广场的点的坐标为（1.5，1.5）表示庐江汽车站的点的坐标为（﹣4.5，﹣7.5）时，表示周瑜文化园的点的坐标为（19.5，﹣10.5）．
上述结论中，所有符合题意结论的序号是（）

A、①②③ B、②③④ C、①④ D、①②③④

查看试题解析

二、填空题

11. 下列各数： $\frac{π}{3}$ ， $\frac{22}{7}$ ， $\sqrt[3]{9}$ ， $\sqrt{\frac{1}{4}}$ ， $0 . \dot{3} \dot{7}$ ， ﹣3.1010010001…（两个1之间的0的个数逐次增加），无理数有个．

查看试题解析
12. 已知直角三角板和直尺如图放置，若∠1=20°，则∠2的度数为．

查看试题解析
13. 如图是一台雷达探测相关目标得到的结果，若记图中目标A的位置为（2，90°），B为（5，30°），C为（5，240°），则目标D的位置表示为．

查看试题解析
14. 有长方形纸片，E，F分别是AD，BC上一点∠DEF＝x（0°＜x＜45°），将纸片沿EF折叠成图1，再沿GF折叠成图2．

(1)、如图1，当x＝32°时， $∠ F G D^{'}$ ＝度；

(2)、如图2，作∠MGF的平分线GP交直线EF于点P，则∠GPE＝（用x的式子表示）．

查看试题解析

三、解答题

15.

(1)、计算：﹣1²⁰²¹+ $\sqrt{9}$ + $\sqrt[3]{2 \frac{10}{27}}$ ；

(2)、求所给式子中x的值（x+1）²﹣2＝23．

查看试题解析
16. 已知点P（﹣3a﹣4，2+a），根据下列条件，分别求点P的坐标：

(1)、点P在x轴上；

(2)、若Q（5，8），且PQ∥y轴．

查看试题解析
17. 观察下列一组等式：
第①个 $\sqrt{2 + \frac{2}{3}} = 2 \sqrt{\frac{2}{3}}$ ；
第②个 $\sqrt{3 + \frac{3}{8}} = 3 \sqrt{\frac{3}{8}}$ ；
第③个 $\sqrt{4 + \frac{4}{15}} = 4 \sqrt{\frac{4}{15}}$ ；
第④个 $\sqrt{5 + \frac{5}{24}} = 5 \sqrt{\frac{5}{24}}$ ；
根据你观察到的规律，完成以下问题：

(1)、第⑤个等式为．

(2)、用n的式子表示第n个等式为．

查看试题解析
18. 如图，直线AB，CD相交于O，OE平分∠AOC，OF⊥OE，若∠BOD＝40°，求∠DOF的度数．

查看试题解析
19. 完成下列证明过程，并在括号内填上依据．
如图，点E在AB上，点F在CD上，∠1＝∠2，∠B＝∠C，求证AB∥CD．
证明：∵∠1＝∠2（已知），∠1＝∠4（                  ▲                   ，
∴∠2＝∠4（等量代换），
∴                  ▲                  （                  ▲                  ）．
∴∠3＝∠C（                  ▲                  ）．
又∵∠B＝∠C（已知），
∴∠3＝∠B（等量代换），
∴AB∥CD（                  ▲                  ）．

查看试题解析
20. 已知x﹣2的平方根是±1，2x+y+17的立方根是3，

(1)、求x，y的值；

(2)、求x²+y²的平方根；

(3)、若将平面坐标系内点P（x，y）先向左再向下分别平移 $\sqrt{10}$ 个单位，则对应点 $P^{'}$ 在第象限．

查看试题解析
21. 如图所示， $△$ ABC三个顶点坐标分别为A（﹣1，4），B（-6，2），C（﹣4，﹣2），将 $△$ ABC沿x轴向右平移6个单位再沿y轴向下平移3个单位得到 $△$ A₁B₁C₁ ．

(1)、请在坐标系中画出 $△$ A₁B₁C₁；

(2)、连接AA₁ ， CC₁ ，线段AA₁ ， CC₁关系为．

(3)、若P（a，b）为 $△$ ABC内一点，则经过平移后对应点P₁坐标为．

(4)、 $△$ A₁B₁C₁的面积为．

查看试题解析
22. 如图，∠1+∠2＝180°，∠3＝∠B．

(1)、判断∠A与∠CEF是否相等，并说明理由．

(2)、若∠AED＝80°，求∠C的度数．

查看试题解析
23. 直线AB∥CD，点P为平面内一点，连接AP，CP．

(1)、如图①，点P在直线AB，CD之间，当∠BAP＝60°，∠DCP＝20°时，求∠APC的度数；

(2)、如图②，点P在直线AB，CD之间，∠BAP与∠DCP的角平分线相交于K，写出∠AKC与∠APC之间的数量关系，并说明理由；

(3)、如图③，点P在直线CD下方，当∠BAK＝ $\frac{2}{3}$ ∠BAP，∠DCK＝ $\frac{2}{3}$ ∠DCP时，写出∠AKC与∠APC之间的数量关系，并说明理由．

查看试题解析

∠APN度数（°）	52.3	69.3	88.8	93.5	105.8	117.8
AP长度（m）	693	587	549	550	570	620