天津市南开区2020-2021学年八年级下学期期中数学试卷
试卷更新日期:2022-03-15 类型:期中考试
一、单选题
-
1. 在△ABC中,∠A,∠B,∠C的对应边分别是a,b,c,若∠B=90°,则下列等式中成立的是( )A、a2+b2=c2 B、b2+c2=a2 C、a2+c2=b2 D、c2﹣a2=b22. 在函数 中,自变量 的取值范围是( )A、 B、 C、 且 D、3. 下列各曲线中不能表示y是x的函数的是( )A、
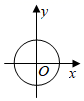 B、
B、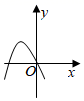 C、
C、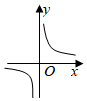 D、
D、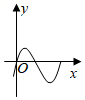 4. 已知三角形的三边长a、b、c满足 + +|c- |=0,则三角形的形状是( )A、等腰三角形 B、等边三角形 C、直角三角形 D、不能确定5. 如图,在 中, , , ,D、E分别是 、 的中点,则 的长为( )
4. 已知三角形的三边长a、b、c满足 + +|c- |=0,则三角形的形状是( )A、等腰三角形 B、等边三角形 C、直角三角形 D、不能确定5. 如图,在 中, , , ,D、E分别是 、 的中点,则 的长为( )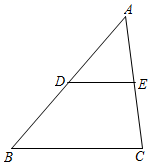 A、3 B、2.5 C、4 D、3.56. 下列说法正确的是( )A、对角线互相垂直平分的四边形是正方形 B、对角线相等的四边形是矩形 C、对角线互相垂直的四边形是菱形 D、对角线互相平分的四边形是平行四边形7. 如图,矩形ABCD中,对角线AC,BD交于点O,DE⊥AC于E,且∠ADE:∠EDC=3:2,则∠COD的度数为( )
A、3 B、2.5 C、4 D、3.56. 下列说法正确的是( )A、对角线互相垂直平分的四边形是正方形 B、对角线相等的四边形是矩形 C、对角线互相垂直的四边形是菱形 D、对角线互相平分的四边形是平行四边形7. 如图,矩形ABCD中,对角线AC,BD交于点O,DE⊥AC于E,且∠ADE:∠EDC=3:2,则∠COD的度数为( )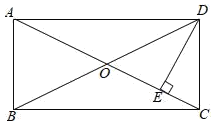 A、54° B、60° C、65° D、72°8. 如图,在四边形 中,对角线 , 相交于点 ,且 , .若要使四边形 为矩形,则可以添加的条件是( )
A、54° B、60° C、65° D、72°8. 如图,在四边形 中,对角线 , 相交于点 ,且 , .若要使四边形 为矩形,则可以添加的条件是( )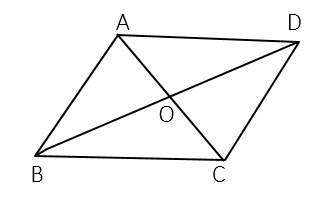 A、 B、 C、 D、9. 已知林茂的家、体育场、文具店在同一直线上,图中的信息反映的过程是:林茂从家跑步去体育场,在体育场锻炼了一阵后又走到文具店买笔,然后再走回家.图中x表示时间,y表示林茂离家的距离.依据图中的信息,下列说法不正确的是( )
A、 B、 C、 D、9. 已知林茂的家、体育场、文具店在同一直线上,图中的信息反映的过程是:林茂从家跑步去体育场,在体育场锻炼了一阵后又走到文具店买笔,然后再走回家.图中x表示时间,y表示林茂离家的距离.依据图中的信息,下列说法不正确的是( )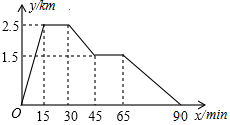 A、体育场离林茂家 B、体育场离文具店 C、林茂从体育场出发到文具店的平均速度是 D、林茂从文具店回家的平均速度是10. 如图,两把完全一样的直尺叠放在一起,重合的部分构成一个四边形,这个四边形一定是( )
A、体育场离林茂家 B、体育场离文具店 C、林茂从体育场出发到文具店的平均速度是 D、林茂从文具店回家的平均速度是10. 如图,两把完全一样的直尺叠放在一起,重合的部分构成一个四边形,这个四边形一定是( )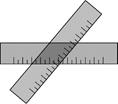 A、矩形 B、菱形 C、正方形 D、无法判断11. 如图,在Rt△ABC中,∠C=90°,AC=8,BC=6,按图中所示方法将△BCD沿BD折叠,使点C落在边AB上的点C′处,则点D到AB的距离( )
A、矩形 B、菱形 C、正方形 D、无法判断11. 如图,在Rt△ABC中,∠C=90°,AC=8,BC=6,按图中所示方法将△BCD沿BD折叠,使点C落在边AB上的点C′处,则点D到AB的距离( ) A、3 B、4 C、5 D、12. 在如图的网格中,每个小正方形的边长为1,A、B、C三点均在正方形格点上,若 是 的高,则 的长为( )
A、3 B、4 C、5 D、12. 在如图的网格中,每个小正方形的边长为1,A、B、C三点均在正方形格点上,若 是 的高,则 的长为( ) A、 B、 C、 D、2
A、 B、 C、 D、2二、填空题
-
13. 如图,在数轴上点A表示的实数是 .
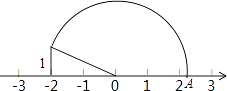 14. 在平面直角坐标系中,已知点A的坐标为 ,则A到原点O的距离为15. 如图,已知的周长为 , , , 则的面积为 .
14. 在平面直角坐标系中,已知点A的坐标为 ,则A到原点O的距离为15. 如图,已知的周长为 , , , 则的面积为 .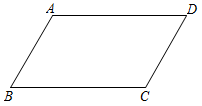 16. 若正方形 的对角线 的长为4,则该正方形的面积为.17. 等腰三角形的两条中位线分别为3和5,则等腰三角形的周长为 .18. 小亮从家骑车上学,先经过一段平路到达A地后,再上坡到达B地,最后下坡到达学校,所行驶路程s(千米)与时间t(分钟)的关系如图所示.如果返回时,上坡、下坡、平路的速度仍然保持不变,那么他从学校回到家需要的时间是分钟.
16. 若正方形 的对角线 的长为4,则该正方形的面积为.17. 等腰三角形的两条中位线分别为3和5,则等腰三角形的周长为 .18. 小亮从家骑车上学,先经过一段平路到达A地后,再上坡到达B地,最后下坡到达学校,所行驶路程s(千米)与时间t(分钟)的关系如图所示.如果返回时,上坡、下坡、平路的速度仍然保持不变,那么他从学校回到家需要的时间是分钟.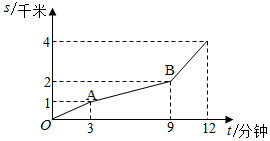
三、解答题
-
19. 如图,在由边长为1的小正方形组成的网格中,△ABC的三个顶点均在格点上,请按要求完成下列各题:
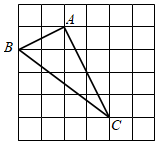 (1)、在网格中画出平行四边形ABCD;(2)、线段AC的长为 , CD的长为 , AD的长为 , △ACD为 三角形,平行四边形ABCD的面积为 .20. 如图,已知一块四边形的草地ABCD,其中∠B=90°,AB=20m,BC=15m,CD=7m,DA=24m,求这块草地的面积.
(1)、在网格中画出平行四边形ABCD;(2)、线段AC的长为 , CD的长为 , AD的长为 , △ACD为 三角形,平行四边形ABCD的面积为 .20. 如图,已知一块四边形的草地ABCD,其中∠B=90°,AB=20m,BC=15m,CD=7m,DA=24m,求这块草地的面积.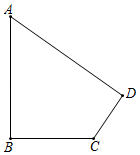 21. 如图,正方形ABCD和正方形CEFG,点G在CD上,AB=5,CE=2,T为AF的中点,求CT的长.
21. 如图,正方形ABCD和正方形CEFG,点G在CD上,AB=5,CE=2,T为AF的中点,求CT的长.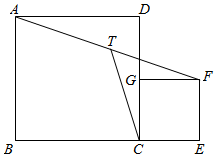 22. 如图,在Rt△ABC中,∠BAC=90°,AB=6,AC=8,P为边BC上一动点,PE⊥AB于E,PF⊥AC于F,M为EF的中点,求AM的最小值.
22. 如图,在Rt△ABC中,∠BAC=90°,AB=6,AC=8,P为边BC上一动点,PE⊥AB于E,PF⊥AC于F,M为EF的中点,求AM的最小值. 23. 在一定弹性限度内,弹簧挂上物体后会伸长.现测得一弹簧长度y(cm)与所挂物体质量x(kg)有如下关系:(已知在弹性限度内该弹簧悬挂物体后的最大长度为21cm.)
23. 在一定弹性限度内,弹簧挂上物体后会伸长.现测得一弹簧长度y(cm)与所挂物体质量x(kg)有如下关系:(已知在弹性限度内该弹簧悬挂物体后的最大长度为21cm.)所挂物体质量x/kg
0
1
2
3
4
5
6
弹簧长度y/cm
12
12.5
13
13.5
14
14.5
15
(1)、有下列说法:①x与y都是变量,且x是自变量,y是x的函数;②所挂物体质量为6kg时,弹簧伸长了3cm;③弹簧不挂重物时的长度为6cm;④物体质量每增加1kg,弹簧长度y增加0.5cm.上述说法中不正确的是 (填序号)(2)、请写出弹簧长度y(cm)与所挂物体质量x(kg)之间的关系式及自变量的取值范围.(3)、预测当所挂物体质量为10kg时,弹簧长度是多少?(4)、当弹簧长度为20cm时,求所挂物体的质量.24. 如图,在菱形ABCD中,AE⊥BC于点E. (1)、如图1,若∠BAE=30°,AE=3,求菱形ABCD的周长及面积;(2)、如图2,作AF⊥CD于点F,连接EF,BD,求证:EF∥BD;(3)、如图3,设AE与对角线BD相交于点G,若CE=4,BE=8,四边形CDGE和△AGD的面积分别是S1和S2 , 求S1﹣S2的值.
(1)、如图1,若∠BAE=30°,AE=3,求菱形ABCD的周长及面积;(2)、如图2,作AF⊥CD于点F,连接EF,BD,求证:EF∥BD;(3)、如图3,设AE与对角线BD相交于点G,若CE=4,BE=8,四边形CDGE和△AGD的面积分别是S1和S2 , 求S1﹣S2的值.