天津市津南区南部学区2020-2021学年八年级下学期期中数学试卷
试卷更新日期:2022-03-15 类型:期中考试
一、单选题
-
1. 式子 在实数范围内有意义,则x的取值范围是( )A、 B、 C、 D、2. 下列二次根式是最简二次根式的是( )A、 B、 C、 D、3. 下面计算正确的是( )A、4+=4 B、÷=3 C、·= D、=±24. 下列各组数中,以a、b、c为边的三角形不是直角三角形的是( )A、a=1、b=2、c= B、a=1.5、b=2、c=3 C、a=6、b=8、c= 10 D、a=3、b=4、c=55. 在Rt△ABC中,两条直角边的长分别为5和12,则斜边的长为( )A、6 B、7 C、10 D、136. 如图,将□ABCD的一边BC延长至点E , 若∠A=110°,则∠1等于( )
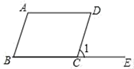 A、110° B、35° C、70° D、55°7. 下列命题不正确的是( )A、两组对边分别平行的四边形是平行四边形 B、两组对边分别相等的四边形是平行四边形 C、一组对边平行,另一组对边相等的四边形是平行四边形 D、对角线互相平分的四边形是平行四边形8. 在四边形中,对角线 , 相交于点O, , , 添加下列条件,不能判定四边形是菱形的是( ).A、 B、 C、 D、9. 如图,正方形网格中的△ABC,若小方格边长为1,则△ABC的形状为( )
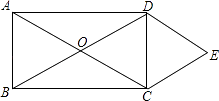
A、110° B、35° C、70° D、55°7. 下列命题不正确的是( )A、两组对边分别平行的四边形是平行四边形 B、两组对边分别相等的四边形是平行四边形 C、一组对边平行,另一组对边相等的四边形是平行四边形 D、对角线互相平分的四边形是平行四边形8. 在四边形中,对角线 , 相交于点O, , , 添加下列条件,不能判定四边形是菱形的是( ).A、 B、 C、 D、9. 如图,正方形网格中的△ABC,若小方格边长为1,则△ABC的形状为( )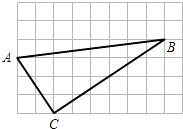 A、直角三角形 B、锐角三角形 C、钝角三角形 D、以上答案都不对10. 如图,在菱形 中,对角线 相交于点 为 中点, .则线段 的长为:( )
A、直角三角形 B、锐角三角形 C、钝角三角形 D、以上答案都不对10. 如图,在菱形 中,对角线 相交于点 为 中点, .则线段 的长为:( ) A、 B、 C、3 D、511. 正方形有而矩形不一定有的性质是( )A、四个角都是直角 B、对角线相等 C、对角线互相平分 D、对角线互相垂直12. 如图,已知矩形纸片ABCD,AB=4,BC=3,点P在BC边上,将△CDP沿DP折叠,点C落在点E处,PE、DE分别交AB于点O、F,且OP=OF,则DF的长为( )
A、 B、 C、3 D、511. 正方形有而矩形不一定有的性质是( )A、四个角都是直角 B、对角线相等 C、对角线互相平分 D、对角线互相垂直12. 如图,已知矩形纸片ABCD,AB=4,BC=3,点P在BC边上,将△CDP沿DP折叠,点C落在点E处,PE、DE分别交AB于点O、F,且OP=OF,则DF的长为( )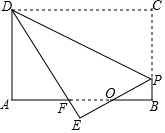 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
13. 化简二次根式 的结果是.14. 一个直角三角形两边长为6和8,则第三边长为 .15. 如图,在四边形中, , , 若再添加一个条件,就能推出四边形是矩形,你所添加的条件是 . (写出一种情况即可).
 16. 如图,在校园内有两棵树相距12米,一棵树高14米,另一棵树高9米,一只小鸟从一棵树的顶端飞到另一棵树的顶端,小鸟至少要飞米.
16. 如图,在校园内有两棵树相距12米,一棵树高14米,另一棵树高9米,一只小鸟从一棵树的顶端飞到另一棵树的顶端,小鸟至少要飞米.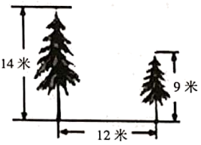 17. 如图,已知在△ABC中,D、E分别是AB、AC的中点,F、G分别是AD、AE的中点,且FG=2cm,则BC的长度是cm.
17. 如图,已知在△ABC中,D、E分别是AB、AC的中点,F、G分别是AD、AE的中点,且FG=2cm,则BC的长度是cm. 18. 如图,正方形ABCD和正方形EFCG的边长分别为3和1,点F,G分别在边BC,CD上,P为AE的中点,连接PG,则PG的长为 .
18. 如图,正方形ABCD和正方形EFCG的边长分别为3和1,点F,G分别在边BC,CD上,P为AE的中点,连接PG,则PG的长为 .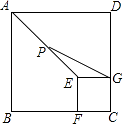
三、解答题
-
19. 计算(1)、(2)、20. 已知:如图,四边形ABCD中,AB⊥BC,AB=1,BC=2,CD=2,AD=3,求四边形ABCD的面积.
 21. 一架云梯长25m,如图所示斜靠在一而墙上,梯子底端C离墙7m.
21. 一架云梯长25m,如图所示斜靠在一而墙上,梯子底端C离墙7m.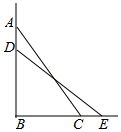 (1)、这个梯子的顶端A距地面有多高?(2)、如果梯子的顶端下滑了4 m,那么梯子的底部在水平方向滑动了多少米?22. 如图,在▱ABCD中,点E、F分别在边BC和AD上,且BE=DF.
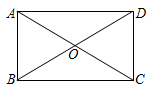
(1)、这个梯子的顶端A距地面有多高?(2)、如果梯子的顶端下滑了4 m,那么梯子的底部在水平方向滑动了多少米?22. 如图,在▱ABCD中,点E、F分别在边BC和AD上,且BE=DF.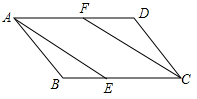 (1)、求证:△ABE≌△CDF.(2)、求证:四边形AECF是平行四边形.23. 如图,矩形ABCD的对角线AC、BD相交于点O,AB=5cm,∠BOC=120°,求矩形对角线的长.
(1)、求证:△ABE≌△CDF.(2)、求证:四边形AECF是平行四边形.23. 如图,矩形ABCD的对角线AC、BD相交于点O,AB=5cm,∠BOC=120°,求矩形对角线的长.