天津市河西区2020-2021学年八年级下学期期中考试数学试题
试卷更新日期:2022-03-15 类型:期中考试
一、单选题
-
1. 计算的结果为( )A、 B、 C、 D、2. 若式子 在实数范围内有意义,则x的取值范围是( )A、x≥3 B、x≤3 C、x>3 D、x<33. 由下列长度组成的各组线段中,不能组成直角三角形的是( )A、7cm,24cm,25cm B、1.5cm,2cm,2.5cm C、50cm,30cm,40cm D、cm,cm,1cm4. 下列计算不正确的是( )A、 B、 C、 D、5. 下列命题中,是假命题的是( )A、对角线互相平分的四边形是平行四边形 B、对角线互相垂直的平行四边形是菱形 C、对角线相等的四边形是矩形 D、对角线互相垂直平分且相等的四边形是正方形6. 点在平面直角坐标系中,则点到原点的距离是( )A、2 B、 C、 D、7. 已知是整数,正整数n的最小值为( )A、96 B、6 C、24 D、28. 如图,在中,已知 , 垂足为E.如果 , 则的度数是( )
 A、 B、 C、 D、9. 如图,四边形中, , , , , 且 , 则四边形的面积为( )
A、 B、 C、 D、9. 如图,四边形中, , , , , 且 , 则四边形的面积为( ) A、 B、 C、 D、10. 将5个边长为2cm的正方形按如图所示摆放,点 , , , 是正方形的中心,则这个正方形重叠部分的面积和为( )
A、 B、 C、 D、10. 将5个边长为2cm的正方形按如图所示摆放,点 , , , 是正方形的中心,则这个正方形重叠部分的面积和为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 计算 的结果是.12. 边长为的正方形的对角线的长度为 .13. 若平行四边形中相邻两个内角的度数比为1:3,则其中较小的内角是度.14. 如图,在菱形中,对角线相交于点O.若 , , 则的周长是 .
 15. 如图,O是坐标原点,菱形的顶点A的坐标为 , 顶点C在x轴的正半轴上,则点B的坐标为 .
15. 如图,O是坐标原点,菱形的顶点A的坐标为 , 顶点C在x轴的正半轴上,则点B的坐标为 . 16. 如图,是由12个边长相等的正三角形镶嵌而成的平面图形,则图中的平行四边形共有个.
16. 如图,是由12个边长相等的正三角形镶嵌而成的平面图形,则图中的平行四边形共有个.
三、解答题
-
17. 计算:(1)、(2)、18. 已知 , 求 的值.19. 已知:如图,在平行四边形中,E,F分别是 , 的中点.求证:四边形是平行四边形.
 20. 如图,折叠矩形的一边AD,使点D落在BC边的点F处,已知AB=8cm,BC=10cm,求EC的长.
20. 如图,折叠矩形的一边AD,使点D落在BC边的点F处,已知AB=8cm,BC=10cm,求EC的长. 21. 如图,在四边形 中, , ,对角线 , 交于点 , 平分 ,过点 作 交 的延长线于点 ,连接 .
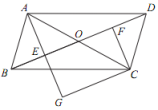
21. 如图,在四边形 中, , ,对角线 , 交于点 , 平分 ,过点 作 交 的延长线于点 ,连接 . (1)、求证:四边形 是菱形;(2)、若 , ,求 的长.
(1)、求证:四边形 是菱形;(2)、若 , ,求 的长.