天津市东丽区2020-2021学年八年级下学期期中数学试题
试卷更新日期：2022-03-15 类型：期中考试
一、单选题
-
1. 二次根式有意义的条件是（ ）。
A、x>3 B、x>-3 C、x≥-3 D、x≥32. 如果下列各组数是三角形的三边，那么不能组成直角三角形的一组数是（ ）A、2，3，4 B、3，4，5 C、6，8，10 D、5，12，133. 下列式子中，属于最简二次根式的是（ ）A、 B、 C、 D、4. 如图，△ABC中，已知AB＝8，∠C＝90°，∠A＝30°，DE是中位线，则DE的长为（ ）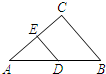
A、4 B、3 C、2 3 D、25. 计算 的结果为（ ）A、 B、 C、 D、6. 已知平行四边形ABCD，下列条件中，不能判定这个平行四边形为矩形的是（ ）A、∠A=∠B B、∠A=∠C C、AC=BD D、AB⊥BC7. 估算 的值在（ ）A、1和2之间 B、2和3之间 C、3和4之间 D、4和5之间8. 在平行四边形ABCD中，∠B＝110°，延长AD至F，延长CD至E，连接EF，则∠E+∠F＝（ ）
A、110° B、30° C、50° D、70°9. 如图，矩形ABCD的对角线AC＝8cm，∠AOD＝120°，则AB的长为（ ）
A、5cm B、4cm C、3cm D、2cm10.如图，已知某广场菱形花坛ABCD的周长是24米，∠BAD=60°，则花坛对角线AC的长等于（ ）
A、6 米 B、6米 C、3 米 D、3米11. △ABC中，AB＝15，AC＝13，高AD＝12，则△ABC的周长为（ ）A、42 B、32 C、42 或 32 D、37 或 3312. 如图，在等腰直角三角形ABC中， ， ， 点D是边AC的中点，连接BD，点E为AC延长线上的一点，连接BE， ， 则CE的长为（ ）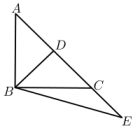
A、 B、 C、 D、二、填空题
-
13. 化简 的结果为.14. 平面直角坐标系中，点P的坐标为（3，﹣5），则OP的长为 ．15. 如图，在 ▱ ABCD中，AD=6，AB=4，DE平分∠ADC交BC于点E，则BE的长是 ．
16. 在如图的网格中，每个小正方形的边长为1，A、B、C三点均在正方形格点上，若AD是△ABC的高，则AD的长为 ．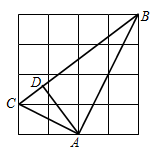
17. 实数a在数轴上的位置如图所示，则﹣化简后为 ．
18. 将矩形纸片ABCD按如图所示的方式折叠，恰好得到菱形AECF．若AB＝3，则菱形AECF的面积为 ．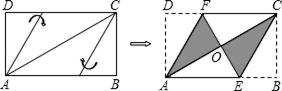
三、解答题
-
19. 计算： .20. 如图，已知在△ABC中，CD⊥AB于D，AC＝8，BC＝5，DB＝3．
(1)、求DC的长；(2)、求AB的长．21. 如图，在▱ABCD中，点E，F是对角线BD上的两点，且BE＝DF，
求证：
(1)、△ABE≌△CDF；(2)、AE∥CF22. 如图，△ABC中，AC=BC，CD⊥AB于点D，四边形DBCE是平行四边形.求证：四边形ADCE是矩形.
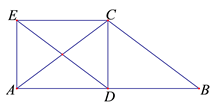23. 如图，O为矩形ABCD对角线的交点，DE∥AC，CE∥BD．
(1)、试判断四边形OCED的形状，并说明理由；(2)、若AB=6，BC=8，求四边形OCED的面积．
