山西省晋中市灵石县2020-2021学年八年级下学期期中数学试题
试卷更新日期:2022-03-15 类型:期中考试
一、单选题
-
1. 2020年太原将正式步入地铁时代,太原轨道交通近期建设的1,2,3号线在全国是第338条线路,下面是中国四个城市的地铁图标,其中是中心对称图形的是( ).A、
 B、
B、 C、
C、 D、
D、 2. 下列多项式中,能分解出因式的是( )A、 B、 C、 D、3. 如图:一把直尺压住射线OB,另一把直尺压住射线OA并且与第一把直尺交于点P,小明说:“射线OP就是∠BOA的角平分线.”他这样做的依据是( )
2. 下列多项式中,能分解出因式的是( )A、 B、 C、 D、3. 如图:一把直尺压住射线OB,另一把直尺压住射线OA并且与第一把直尺交于点P,小明说:“射线OP就是∠BOA的角平分线.”他这样做的依据是( ) A、角平分线上的点到这个角两边的距离相等 B、角的内部到角的两边的距离相等的点在角的平分线上 C、三角形三条角平分线的交点到三条边的距离相等 D、以上均不符合题意4. 如图,在 中, ,则 的度数为( )
A、角平分线上的点到这个角两边的距离相等 B、角的内部到角的两边的距离相等的点在角的平分线上 C、三角形三条角平分线的交点到三条边的距离相等 D、以上均不符合题意4. 如图,在 中, ,则 的度数为( ) A、 B、 C、 D、5. 古埃及人曾经用如图所示的方法画直角:把一根长绳打上等距离的13个结,然后以3个结间距,4个结间距,5个结间距的长度为边长,用木桩钉成一个三角形,其中一角便是直角,这样做的道理是( )
A、 B、 C、 D、5. 古埃及人曾经用如图所示的方法画直角:把一根长绳打上等距离的13个结,然后以3个结间距,4个结间距,5个结间距的长度为边长,用木桩钉成一个三角形,其中一角便是直角,这样做的道理是( ) A、直角三角形两个锐角互余 B、三角形内角和等于180° C、三角形两边之和大于第三边,两边之差小于第三边 D、如果三角形两边的平方和等于第三边的平方,那么这个三角形是直角三角形6. 如图,△ABC沿线段BA方向平移得到△DEF,若AB=6,AE=2,则平移的距离为( )
A、直角三角形两个锐角互余 B、三角形内角和等于180° C、三角形两边之和大于第三边,两边之差小于第三边 D、如果三角形两边的平方和等于第三边的平方,那么这个三角形是直角三角形6. 如图,△ABC沿线段BA方向平移得到△DEF,若AB=6,AE=2,则平移的距离为( )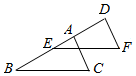 A、2 B、4 C、6 D、87. 下列分解因式正确的是( )A、-x2+4x=-x(x+4) B、x2+xy+x=x(x+y) C、-x2+y2=(x+y)(y-x) D、x2-4x+4=(x+2)(x-2)8. 如图,教室里有一只倒地的装垃圾的灰斗,BC与地面的夹角为50°,∠C=25°,小贤同学将它绕点C旋转一定角度,扶起平放在地面上(如图),则灰斗柄AB绕点C转动的角度为( )
A、2 B、4 C、6 D、87. 下列分解因式正确的是( )A、-x2+4x=-x(x+4) B、x2+xy+x=x(x+y) C、-x2+y2=(x+y)(y-x) D、x2-4x+4=(x+2)(x-2)8. 如图,教室里有一只倒地的装垃圾的灰斗,BC与地面的夹角为50°,∠C=25°,小贤同学将它绕点C旋转一定角度,扶起平放在地面上(如图),则灰斗柄AB绕点C转动的角度为( ) A、75° B、25° C、115° D、105°9. 如图,在△ABC中,∠BAC=80°,AB边的垂直平分线交AB于点D , 交BC于点E , AC边的垂直平分线交AC于点F , 交BC于点G , 连接AE , AG . 则∠EAG的度数为( )
A、75° B、25° C、115° D、105°9. 如图,在△ABC中,∠BAC=80°,AB边的垂直平分线交AB于点D , 交BC于点E , AC边的垂直平分线交AC于点F , 交BC于点G , 连接AE , AG . 则∠EAG的度数为( ) A、15° B、20° C、25° D、30°10. 在△ABC中,AB=AC﹥BC,D为BC的中点,动点P从点B出发,沿B→A→C的方向运动.运动过程中使得△PBD为等腰三角形的P的位置有( )个A、2个 B、4个 C、6个 D、8个
A、15° B、20° C、25° D、30°10. 在△ABC中,AB=AC﹥BC,D为BC的中点,动点P从点B出发,沿B→A→C的方向运动.运动过程中使得△PBD为等腰三角形的P的位置有( )个A、2个 B、4个 C、6个 D、8个二、填空题
-
11. 命题“等腰三角形的两腰上的高线相等” 的逆命题是: .12. 如图所示的美丽图案,绕着它的旋转中心至少旋转度,能够与原来的图象重合.
 13. 如图,点O在内,且到三边的距离相等,若∠A=55°,则∠BOC= .
13. 如图,点O在内,且到三边的距离相等,若∠A=55°,则∠BOC= . 14. 如图,点 分别是等边三角形 的边 的点,且 与 相交于点 .则 的度数为 .
14. 如图,点 分别是等边三角形 的边 的点,且 与 相交于点 .则 的度数为 .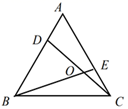 15. 如图,在中, , , 点D是线段上一点,将沿折叠,得到 , 当时,的长为 .
15. 如图,在中, , , 点D是线段上一点,将沿折叠,得到 , 当时,的长为 .
三、解答题
-
16. 下面是小华同学分解因式的过程,请认真阅读,并回答下列问题.
解:原式①
②
③
(1)、任务一:以上解答过程从第步开始出现错误.(2)、任务二:请你写出正确的解答过程.17. 在直角坐标系中,将平移后得到 , 它们的三个顶点坐标如表所示:A(a,5)
B(1,3)
C(2,6)
A1(3,3)
B1(5,b)
C1(c,d)
 (1)、观察表中各对应点坐标的变化填空: , ;(2)、向平移个单位长度,再向平移个单位长度可以得到;(3)、①在坐标系中画出及平移后△A1B1C1;
(1)、观察表中各对应点坐标的变化填空: , ;(2)、向平移个单位长度,再向平移个单位长度可以得到;(3)、①在坐标系中画出及平移后△A1B1C1;②以坐标原点O为旋转中心,将顺时针旋转90°,得到 , 请画出
18. 如图,在 中, , 是 边上的中线, 的垂直平分线分别交 、 、 于点 、 、 ,连接 , . (1)、求证:点 在 的垂直平分线上;(2)、若 ,求 的度数.19.(1)、探究发现:
(1)、求证:点 在 的垂直平分线上;(2)、若 ,求 的度数.19.(1)、探究发现:小明计算下面几个题目
①;②;③;④
后发现,形如的两个多项式相乘,计算结果具有一定的规律,请你帮助小明完善发现的规律:
(2)、面积说明:上面规律是否正确呢?小明利用多项式乘法法则计算 , 发现这个规律是正确的.小明记得学习乘法公式时,除利用多项式乘法法则可以证明公式外,还可以利用图形面积说明乘法公式,于是画出右面图形说明他发现的规律,请你帮助小明补全图中括号的代数式.
 (3)、逆用规律:
(3)、逆用规律:学过因式分解后,小明知道了因式分解与整式乘法是逆变形,他就逆用发现的规律对下面的多项式进行了因式分解,请你用小明发现的规律分解下面因式:.
20. 如图,AD平分∠BAC,DE⊥AB,DF⊥AC,垂足分别为点E,F,DB=DC. (1)、求证:BE=CF;(2)、如果BD//AC,∠DAF=15°,求证:AB=2DF.21. 如图①是实验室中的一种摆动装置,BC在地面上,支架ABC是底边为BC的等腰直角三角形,摆动臂AD可绕点A旋转,摆动臂DM可绕点D旋转,AD=13,DM=5.
(1)、求证:BE=CF;(2)、如果BD//AC,∠DAF=15°,求证:AB=2DF.21. 如图①是实验室中的一种摆动装置,BC在地面上,支架ABC是底边为BC的等腰直角三角形,摆动臂AD可绕点A旋转,摆动臂DM可绕点D旋转,AD=13,DM=5. (1)、在旋转过程中.
(1)、在旋转过程中.①当A,D,M三点在同一直线上时,求AM的长;
②当A,D,M三点为同一直角三角形的顶点时,求AM的长;
(2)、若摆动臂AD顺时针旋转90°,点D的位置由△ABC外的点D1转到其内的点D2处,连接D1D2 . 如图②,此时∠AD2C=135°,CD2=20,求BD2的长.22. 综合与实践【问题情境】
在数学综合实践课上,老师让同学用两张全等的等腰三角形纸片进行拼摆,并探究摆放后所构成的图形之间的关系.如图1, , AB=AC,DE=DF.
【操作发现】
 (1)、勤奋小组的同学把这两张纸片完全重合,点A与点D重合,将 绕点D逆时针方向旋转到如图2的位置,连接BE和CF.他们发现BE与CF之间存在着一定的数量关系,请写出这些关系并说明理由;(2)、创新小组的同学在勤奋小组的启发下,把 垂直翻转,再平移使得点E与点A重合,点D与点C重合,再将 沿射线CA的方向向上平移到图3的位置,连接BE和CF,他们发现了BE和CF之间的数量和位置关系,请写出这些关系并说明理由;(3)、请你参照以上操作,将图1中的 在同一平面内进行平移、旋转、翻转等图形变换,构成一种与图2和图3都不相同的图形,在图4中画出构造出的新图形,标明字母,说明构图方法,写出你发现的结论,不必证明.23. 如图, 是等边三角形,AB=6,P是AC边上一动点,由A向C运动(与A、C不重合),Q是CB延长线上一动点,由B向CB延长线方向运动(Q不与B重合),已知点P、Q都以每秒 的速度同时开始运动,连接PQ交AB于D.
(1)、勤奋小组的同学把这两张纸片完全重合,点A与点D重合,将 绕点D逆时针方向旋转到如图2的位置,连接BE和CF.他们发现BE与CF之间存在着一定的数量关系,请写出这些关系并说明理由;(2)、创新小组的同学在勤奋小组的启发下,把 垂直翻转,再平移使得点E与点A重合,点D与点C重合,再将 沿射线CA的方向向上平移到图3的位置,连接BE和CF,他们发现了BE和CF之间的数量和位置关系,请写出这些关系并说明理由;(3)、请你参照以上操作,将图1中的 在同一平面内进行平移、旋转、翻转等图形变换,构成一种与图2和图3都不相同的图形,在图4中画出构造出的新图形,标明字母,说明构图方法,写出你发现的结论,不必证明.23. 如图, 是等边三角形,AB=6,P是AC边上一动点,由A向C运动(与A、C不重合),Q是CB延长线上一动点,由B向CB延长线方向运动(Q不与B重合),已知点P、Q都以每秒 的速度同时开始运动,连接PQ交AB于D. (1)、运动几秒后, 为直角三角形?(2)、求证:在运动过程中,点D始终为线段PQ的中点;(3)、过P作PE⊥AB于E,在运动过程中线段ED的长是否发生变化?如果不变,直接写出线段ED的长;如果变化请说明理由.
(1)、运动几秒后, 为直角三角形?(2)、求证:在运动过程中,点D始终为线段PQ的中点;(3)、过P作PE⊥AB于E,在运动过程中线段ED的长是否发生变化?如果不变,直接写出线段ED的长;如果变化请说明理由.