山西省晋中市介休市2020-2021学年八年级下学期期中数学试题

试卷更新日期：2022-03-15 类型：期中考试

进入出卷网下载

一、单选题

1. 不等式 $x < - 3$ 的解集在数轴上表示正确的是（）

A、 B、 C、 D、

查看试题解析
2. 下面的图形是用数学家名字命名的，其中既是轴对称图形又是中心对称图形的是（）

A、赵爽弦图 B、笛卡尔心形线 C、科克曲线 D、斐波那契螺旋线

查看试题解析
3. 若m＞n，下列不等式不一定成立的是（）

A、m+2＞n+2 B、2m＞2n C、 $\frac{m}{2}$ ＞ $\frac{n}{2}$ D、m²＞n²

查看试题解析
4. 如图，已知∠AOB，以点O为圆心，任意长为半径画弧，交OA于点C，交OB于点D，再分别以C，D为圆心，以大于 $\frac{1}{2}$ CD长为半径画弧，两弧交于点F，作射线OF，点P为OF上一点，PE⊥OB，垂足为点E，若PE＝5，则点P到OA的距离为（）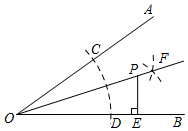

A、5 B、4 C、3 D、 $\sqrt{5}$

查看试题解析
5. 不等式组 ${\begin{array}{l} x - 1 \leq 0 \\ 3 x + 6 > 0 \end{array}$ 的解集为(　　)

A、x≤1 B、x＞﹣2 C、﹣2＜x≤1 D、无解

查看试题解析
6. 如图，将 $△ O A B$ 绕点O逆时针旋转 $70 °$ ，得到 $△ O C D$ ，若 $∠ A = 2 ∠ D = 100 °$ ，则 $α$ 的度数是（）

A、50° B、60° C、40° D、30°

查看试题解析
7. 如图，直线y₁＝kx+2与直线y₂＝mx相交于点P(1，m)，则不等式mx＜kx+2的解集是（）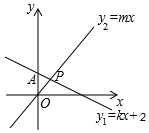

A、x＜0 B、x＜1 C、0＜x＜1 D、x＞1

查看试题解析
8. 如图，在 $Δ A B C$ 中， $A B = A C$ ， $∠ A P B \neq ∠ A P C$ ，求证： $P B \neq P C$ .当用反证法证明时，第一步应假设（）

A、 $A B \neq A C$ B、 $P B = P C$ C、 $∠ A P B = ∠ A P C$ D、 $∠ B \neq ∠ C$

查看试题解析
9. 以如图的右边缘所在直线为轴将该图案向右翻折后，再绕正方形的中心旋转 $18 0^{∘}$ ，所得到的图形是 $($ 　　 $)$

A、 B、 C、 D、

查看试题解析
10. 如图，在 $△ A B C$ 中， $∠ B = 15^{o}$ ， $∠ C = 30^{o}$ ， $M N$ 是 $A B$ 的中垂线， $P Q$ 是 $A C$ 的中垂线，已知 $B C$ 的长为 $3 + \sqrt{3}$ ，则阴影部分的面积为（）

A、 $\sqrt{3}$ B、 $\frac{\sqrt{3}}{2}$ C、 $3$ D、 $\frac{3}{2}$

查看试题解析

二、填空题

11. 请你写出一个满足不等式2x-1＜6的正整数x的值：．

查看试题解析
12. 由于木质的衣架没有柔性，在挂置衣服的时候不太方便操作．小敏设计了一种衣架，在使用时能轻易收拢，然后套进衣服后松开即可，如图1，衣架杆 $O A = O B = 17 c m$ .若衣架收拢时， $∠ A O B = 60 °$ ，如图2，则此时 $A B =$ $c m$ .

查看试题解析
13. 如图1，是某超市自动扶梯，如图2，是其示意图，大厅两层之间的距离 $h = 6.5$ 米，自动扶梯的倾角为30°，若自动扶梯运行速度 $v = 0.5$ 米/秒，则顾客乘自动扶梯上一层楼的时间为秒.

查看试题解析
14. 某品牌运动鞋的进价为150元，出售时标价为225元，由于销路不好，所以商店准备降价促销，但是要保证利润不低于10%，那么商店最多降价元出售．

查看试题解析
15. 如图，把等边△A BC沿着D E折叠，使点A恰好落在BC边上的点P处，且DP⊥BC，若BP=4cm，则EC=cm．

查看试题解析

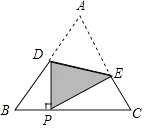
三、解答题

16. 下面是小颖同学解一元一次不等式 $\frac{x + 3}{5} - \frac{2 x - 5}{3} \leq - 1$ 的解答过程，请认真阅读并完成相应任务.
解： $3 (x + 3) - 5 (2 x - 5) \leq - 15$ ，第一步
$3 x + 9 - 10 x - 25 \leq - 15$ ，第二步
$- 7 x \leq 1$ ，第三步
$x \geq - \frac{1}{7}$ ，第四步

(1)、任务一：
填空：
①以上运算步骤中，第步是进行去分母，去分母的依据是；
②第步开始出现错误，这一步不正确的原因是；

(2)、任务二：请直接写出正确的计算结果；

(3)、任务三：除纠正上述不符合题意外，请你根据平时的学习经验，解一元一次不等式时，还需要注意的事项给其他同学提一条建议．

查看试题解析
17. 解下列不等式组，并在数轴上表示出不等式组的解集：

(1)、 ${\begin{array}{l} 4 x \leq 3 (x + 1) \\ 2 x - 1 > - 3 \end{array}$

(2)、 ${\begin{array}{l} 2 (x - 3) < 4 x \\ \frac{5 x - 1}{2} - 1 \leq \frac{2 x + 1}{3} \end{array}$

查看试题解析
18. 如图，在直角坐标系中， $A (- 1 ， 5)$ ， $B (- 1 ， 0)$ ， $C (- 4 ， 3)$ .

(1)、求 $△ A B C$ 的面积；

(2)、若把 $△ A B C$ 向下平移2个单位，再向右平移5个单位得到 $△ A^{'} B^{'} C^{'}$ ，并写出 $C^{'}$ 的坐标.

查看试题解析

19. 阅读理解，并完成任务：

小敏同学在近期作业中遇到一个作图问题，问题如下：

如图，已知 $△ A B C$ 绕某点O逆时针转动一个角度得到 $△ A^{'} B^{'} C^{'}$ ，其中A，B，C的对应点分别是 $A^{'}$ ， $B^{'}$ ， $C^{'}$ ，如何确定旋转中心O位置？

他经过认真思考设计了以下作法，并予以推理：

①连接A、 $A^{'}$ 作线段 $A A^{'}$ 的垂直平分线 $l_{1}$ ；

②连接B， $B^{'}$ 作线段 $B B^{'}$ 的垂直平分线 $l_{2}$ ， $l_{2}$ 与 $l_{1}$ 交于点O.

则点 $O$ 为所求作的旋转中心.

推理过程如下：

∵ $△ A^{'} B^{'} C^{'}$ 是 $△ A B C$ 绕点O旋转而成的

∴ $O A^{^{'}} = O A$ （依据1）

∴点O在线段 $A A^{'}$ 的垂直平分线 $l_{1}$ 上（依据2）

同理可得，点 $O$ 在线段 $B B^{'}$ 的垂直平分线 $l_{2}$ 上

∴点 $O$ 为 $l_{1}$ 与 $l_{2}$ 的交点.

任务：

(1)、请你使用直尺和圆规，补全图形（保留作图痕迹）；

(2)、上述解答过程中的“依据1”“依据2”分别指什么？

“依据1”：.

“依据2”：.

查看试题解析

20. 如图，在 $△ A B C$ 中， $∠ C = 90 °$ ， $A D$ 平分 $∠ C A B$ ，交 $C B$ 于点D，过点D作 $D E ⊥ A B$ 于点E

(1)、求证： $△ A C D ≌ △ A E D$ ；

(2)、若 $∠ B = 30 °$ ， $C D = 5$ ，求 $B D$ 的长．

查看试题解析
21. 应用题：
马铃薯常被人们称之为土豆，是最常见的一种食材，其营养价值很高．为了增加种植效益，农民王大伯因地制宜调整种植结构计划种植马铃薯和蔬菜共15亩，预计每亩的投入与产出如下表：

投入（元）
产出（元）
马铃薯
1000
4500
蔬菜
1200
5300

(1)、如果这15亩地的纯收入要达到5490元，需种植马铃薯和蔬菜各多少亩？

(2)、如果总投入不超过16000元，则最多种植蔬菜多少亩？该情况下15亩地的纯收入是多少？

查看试题解析
22. 综合与探究：
如图1，在 $△ A B C$ 中，已知 $A B = A C$ ， $∠ B A C = 90 °$ ， $B C = 8 c m$ ，点D从点C开始沿射线CB方向以每秒2厘米的速度运动，连接AD，设运动时间为t秒．

(1)、求 $A B$ 的长．

(2)、当t为何值时， $△ A B D$ 为等腰三角形．

查看试题解析
23. 综合与实践：

【问题情境】

在数学综合实践课上，老师让同学用两张全等的等腰三角形纸片进行拼摆，并探究摆放后所构成的图形之间的关系．如图1， $△ A B C ≌ △ D E F$ ， $A B = A C$ ， $D E = D F$ ．

(1)、【猜想探究】
“勤奋小组”的同学把这两张纸片按如图2的方式摆放，点A与点D重合，连接 $B E$ 和 $C F$ ．他们发现 $B E$ 和 $C F$ 之间存在着一定的数量关系，这个关系是．

(2)、【类比验证】
“创新小组”的同学在“勤奋小组”的启发下，把这两张纸片按如图3的方式摆放，点F，A，D，C在同一直线上，连接 $B F$ 和 $C E$ ，他们发现了 $B F$ 和 $C E$ 之间的数量和位置关系，请写出这些关系并说明理由；

(3)、【操作展示】
请你利用 $△ A B C$ 和 $△ D E F$ 纸片进行拼摆，将拼摆出的图形画在图4中（要求不得与图2，图3相同），并根据图形写出一条正确的数学结论．

查看试题解析

	投入（元）	产出（元）
马铃薯	1000	4500
蔬菜	1200	5300