内蒙古自治区呼和浩特市玉泉区2020-2021学年八年级下学期期中数学试题
试卷更新日期:2022-03-15 类型:期中考试
一、单选题
-
1. 式子 在实数范围内有意义,则x的取值范围是( )A、 B、 C、 D、2. 下列式子中,属于最简二次根式的是( )A、 B、 C、 D、3. 下列各式计算正确的是( )A、 B、 C、 D、4. 由下列条件能判定为直角三角形的是( ).A、 B、 C、 , , D、5. 如图,▱ABCD中,AB=3,BC=5,AE平分∠BAD交BC于点E,则CE的长为( )
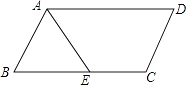 A、1 B、2 C、3 D、46. 下列命题,其中是真命题的为( )A、一组对边平行,另一组对边相等的四边形是平行四边形 B、一组邻边相等的矩形是正方形 C、对角线相等的四边形是矩形 D、对角线互相垂直的四边形是菱形7. 若顺次连接某四边形四边中点所得的四边形是矩形,则原四边形一定是( )A、菱形 B、矩形 C、对角线互相垂直 D、对角线相等8. 如图,边长为4的等边△ABC中,DE为中位线,则四边形BCED的面积为( )
A、1 B、2 C、3 D、46. 下列命题,其中是真命题的为( )A、一组对边平行,另一组对边相等的四边形是平行四边形 B、一组邻边相等的矩形是正方形 C、对角线相等的四边形是矩形 D、对角线互相垂直的四边形是菱形7. 若顺次连接某四边形四边中点所得的四边形是矩形,则原四边形一定是( )A、菱形 B、矩形 C、对角线互相垂直 D、对角线相等8. 如图,边长为4的等边△ABC中,DE为中位线,则四边形BCED的面积为( )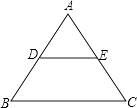 A、 B、 C、 D、9. 如图,在平面直角坐标系中,四边形 为菱形, , , ,则对角线交点 的坐标为( )
A、 B、 C、 D、9. 如图,在平面直角坐标系中,四边形 为菱形, , , ,则对角线交点 的坐标为( )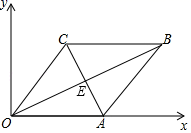 A、 B、 C、 D、10. 有一边长为2的正方形纸片ABCD,先将正方形ABCD对折,设折痕为EF(如图①);再沿过点D的折痕将角A翻折,使得点A落在EF的H上(如图②),折痕交AE于点G,则EG的长度为( )
A、 B、 C、 D、10. 有一边长为2的正方形纸片ABCD,先将正方形ABCD对折,设折痕为EF(如图①);再沿过点D的折痕将角A翻折,使得点A落在EF的H上(如图②),折痕交AE于点G,则EG的长度为( ) A、4﹣6 B、2﹣3 C、8﹣4 D、4﹣2
A、4﹣6 B、2﹣3 C、8﹣4 D、4﹣2二、填空题
-
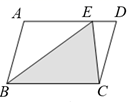
11. 计算:=12. 如图,E为▱ABCD的边AD上任意一点,▱ABCD的面积为6,则图中阴影部分的面积为 .
 13. 如图,在数轴上,先以O为圆心,为半径画圆弧交数轴与A点,再作 , 且 . 若C对应的数是 , 那么数轴上点A所表示的数是 .
13. 如图,在数轴上,先以O为圆心,为半径画圆弧交数轴与A点,再作 , 且 . 若C对应的数是 , 那么数轴上点A所表示的数是 .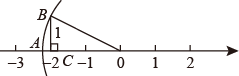 14. 有一根长7cm的木棒,要放进长、宽、高分别为5cm、4cm、3cm的木箱,(填“能”或“不能”)放进去。15. 如图,已知菱形ABCD的周长为16,面积为8 ,E为AB的中点,若P为对角线BD上一动点,则EP+AP的最小值为 .
14. 有一根长7cm的木棒,要放进长、宽、高分别为5cm、4cm、3cm的木箱,(填“能”或“不能”)放进去。15. 如图,已知菱形ABCD的周长为16,面积为8 ,E为AB的中点,若P为对角线BD上一动点,则EP+AP的最小值为 . 16. 观察以下几组勾股数,并寻找规律:①3,4,5;②5,12,13;③7,24,25;④9,40,41;…,请你写出具有以上规律的第⑥组勾股数:
16. 观察以下几组勾股数,并寻找规律:①3,4,5;②5,12,13;③7,24,25;④9,40,41;…,请你写出具有以上规律的第⑥组勾股数:三、解答题
-
17. 计算:(1)、;(2)、 .18. 已知:如图,是平行四边形的对角线上的两点, .

求证:
(1)、;(2)、 .19. 已知a,b,c满足 .(1)、求a、b、c的值(2)、试问以a、b、c为边能否构成三角形?若能构成三角形,请求出三角形的周长,若不能,请说明理由.20. 如图,一架长2.5m的梯子AB斜靠在墙AC上,∠C=90°,此时,梯子的底端B离墙底C的距离BC为0.7m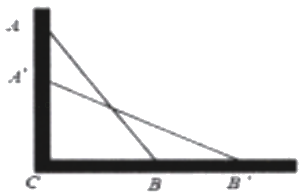 (1)、求此时梯子的顶端A距地面的高度AC;(2)、如果梯子的顶端A下滑了0.9m,那么梯子的底端B在水平方向上向右滑动了多远?21. 已知:如图,在 ▱ ABCD中,AF,BH,CH,DF分别是∠BAD,∠ABC,∠BCD,∠ADC的平分线.求证:四边形EFGH为矩形.
(1)、求此时梯子的顶端A距地面的高度AC;(2)、如果梯子的顶端A下滑了0.9m,那么梯子的底端B在水平方向上向右滑动了多远?21. 已知:如图,在 ▱ ABCD中,AF,BH,CH,DF分别是∠BAD,∠ABC,∠BCD,∠ADC的平分线.求证:四边形EFGH为矩形.

