内蒙古自治区赤峰市松山区2020-2021学年八年级下学期期中数学试题

试卷更新日期：2022-03-15 类型：期中考试

进入出卷网下载

一、单选题

1. 下列二次根式中，最简二次根式的是 $($ $)$

A、 $\sqrt{18}$ B、 $\sqrt{8}$ C、 $\sqrt{10}$ D、 $\sqrt{\frac{1}{2}}$

查看试题解析
2. 下列运算正确的是（）

A、 $\sqrt{2} + \sqrt{3} = \sqrt{5}$ B、 $2 \sqrt{2} \times 3 \sqrt{2} = 6 \sqrt{2}$ C、 $\sqrt{8} \div \sqrt{2} = 2$ D、 $3 \sqrt{2} - \sqrt{2} = 3$

查看试题解析
3. 下列各组数据能构成直角三角形的是（　　）

A、 $\sqrt{3} ， \sqrt{4} ， \sqrt{5}$ B、1， $\sqrt{2} ， \sqrt{3}$ C、5，13，14 D、2，3，4

查看试题解析
4. 如图，在四边形ABCD中，AB∥CD，要使四边形ABCD是平行四边形，下列可添加的条件不正确的是（）

A、AD=BC B、AB=CD C、AD∥BC D、∠A=∠C

查看试题解析
5. 如图，矩形ABCD中，点E在AD上，点F在AB上，且EF⊥EC，EF＝EC，DE＝2，矩形ABCD的周长为16，则AE的长为（　　）

A、3 B、4 C、5 D、6

查看试题解析
6. 如图，已知四边形ABCD中，R，P分别是BC，CD上的点，E，F分别是AP，RP的中点．当点P在CD上从点C向点D移动而点R不动时，以下结论成立的是（　　）

A、线段EF的长逐渐增大 B、线段EF的长逐渐变小 C、线段EF的长不变 D、线段EF的长与点P的位置有关

查看试题解析
7. 式子 $\frac{\sqrt{a + 1}}{a - 2}$ 有意义，则实数a的取值范围是（）

A、a≥﹣1 B、a≠2 C、a≥﹣1且a≠2 D、a＞2

查看试题解析
8. 下列命题中正确的是（　　）

A、对角线互相垂直的四边形是菱形 B、对角线互相平分且相等的四边形是矩形 C、对角线相等的四边形是矩形 D、对角线相等的平行四边形是正方形

查看试题解析
9. 如图△ABC中，AD是角平分线，DE∥AC交AB于E，DF∥AB交AC于F，若AE=4cm，那么四边形AEDF周长为（）

A、12cm B、16cm C、20cm D、22cm

查看试题解析
10. 如图所示，正方形ABCD中，O是对角线AC、BD的交点，过O点作OE⊥OF，分别交AB、BC于E、F，若AE＝4，CF＝3，则EF等于（）

A、7 B、5 C、4 D、3

查看试题解析
11. 若最简二次根式4 $\sqrt{10 - 2 m}$ 与 $\sqrt{m + 4}$ 可以进行合并，则m的值为（　　）

A、﹣1 B、0 C、1 D、2

查看试题解析
12.
如图，将边长为8㎝的正方形ABCD折叠，使点D落在BC边的中点E处，点A落在F处，折痕为MN ，则线段CN的长是（）

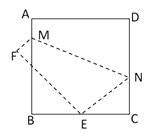A、3cm B、4cm C、5cm D、6cm

查看试题解析
13. 如果ab＞0，a＋b＜0，那么下面各式：① $\sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}}$ ； ② $\sqrt{\frac{a}{b}} \cdot \sqrt{\frac{b}{a}}$ ＝1；③ $\sqrt{a b} \div \sqrt{\frac{a}{b}}$ ＝－b.其中正确的是（）

A、①② B、①③ C、①②③ D、②③

查看试题解析
14. 如果正整数a、b、c满足等式 $a^{2} + b^{2} = c^{2}$ ，那么正整数a、b、c叫做勾股数.某同学将自己探究勾股数的过程列成下表，观察表中每列数的规律，可知x+y的值为（）

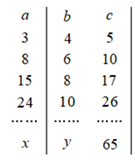A、47 B、62 C、79 D、98

查看试题解析

二、填空题

15. 已知 $\sqrt{9 - x^{2}}$ ＝2﹣x，则x的取值范围是．

查看试题解析
16. 已知 $x, y$ 为实数，且 $y = \sqrt{x^{2} - 9} - \sqrt{9 - x^{2}} + 4$ ，则 $x - y =$ .

查看试题解析
17. 如图，请你添加一个适当的条件，使平行四边形ABCD成为菱形．

查看试题解析
18. 棱长分别为 $5 c m$ ， $4 c m$ 两个正方体如图放置，点P在 $E_{1} F_{1}$ 上，且 $E_{1} P = \frac{1}{4} E_{1} F_{1}$ ，一只蚂蚁如果要沿着长方体的表面从点A爬到点P，需要爬行的最短距离是

查看试题解析

三、解答题

19. 计算： $| 2 \sqrt{2} - 3 | - (- \frac{1}{2})^{- 2} + \sqrt{18}$ ．

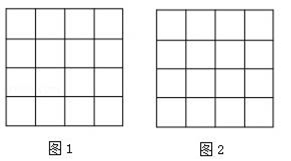
查看试题解析
20. 如图，正方形网格中的每个小正方形边长都是1，每个小格的顶点叫做格点，以格点为顶点分别按下列要求画三角形．

(1)、在图1中，画一个直角三角形，使它们的三边长都是无理数；

(2)、在图2中，画一个正方形，使它的面积是10．

查看试题解析
21. 已知m＝5﹣2 $\sqrt{6}$ ， n＝5+2 $\sqrt{6}$ ．求3m²+5mn+3n²的值．

查看试题解析
22. 已知等腰三角形ABC的底边BC＝4 $\sqrt{13}$ cm，D是腰AB上一点，且CD=12 cm，BD＝8cm．

(1)、求证：CD⊥AB．

(2)、求腰AB的长．

查看试题解析
23. 如图，在四边形 $A B C D$ 中， $A D // B C$ ， $A C$ 与 $B D$ 交于点E ， E是 $B D$ 的中点，延长 $C D$ 到点F ，使 $D F = C D$ ，连接 $A F$ ．

(1)、求证： $A E = C E$ ．

(2)、求证：四边形 $A B D F$ 是平行四边形．

查看试题解析
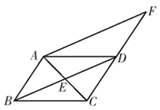24. 阅读材料定义：只有一组对角是直角的四边形叫做损矩形，连接它的两个非直角顶点的线段叫做这个损矩形的直径．

(1)、如图1，损矩形ABCD，∠ABC＝∠ADC＝90°，则该损矩形的直径是线段AC，同时我们还发现损矩形中有公共边的两个三角形角的特点．在公共边的同侧的两个角是相等的．如图1中：△ABC和△ABD有公共边AB，在AB同侧有∠ADB和∠ACB．此时∠ADB＝∠ACB；再比如△ABC和△BCD有公共边BC，在BC同侧有∠BAC和∠BDC，此时∠BAC＝∠BDC，请再找一对这样的角＝．

(2)、应用：
如图2，△ABC中，∠ABC＝90°，以AC为一边向形外作菱形ACEF，D为菱形ACEF的对角线交点．连接BD，当BD平分∠ABC时，判断四边形ACEF为何种特殊的四边形？请说明理由．

查看试题解析
25. 如图1，在△ABC中，点P为BC边中点，直线a绕顶点A旋转．若B、P在直线a的异侧，BM⊥直线a于点M，CN⊥直线a于点N，连接PM、PN；

(1)、延长MP交CN于点E（如图2）．
①求证：△BPM≌△CPE；

②求证：PM＝PN；

(2)、若直线a绕点A旋转到图3的位置时，点B、P在直线a的同侧，其它条件不变．此时PM＝PN还成立吗？若成立，请给予证明；若不成立，请说明理由；

(3)、若直线a绕点A旋转到与BC边平行的位置时，其它条件不变．请直接判断四边形MBCN的形状及此时PM＝PN还成立吗？（不必说明理由）

查看试题解析
26. 阅读理解：
[问题情境]教材中小明用4张全等的直角三角形纸片拼成图1，利用此图，可以验证勾股定理吗？
[探索新知]从面积的角度思考，不难发现：
大正方形的面积＝小正方形的面积+4个直角三角形的面积．
从而得数学等式：（a+b）²＝c²+4× $\frac{1}{2}$ ab，化简证得勾股定理：a²+b²＝c² ．
[初步运用]

(1)、如图1，若b＝2a，求小正方形面积与大正方形面积的比值；

(2)、现将图1中上方的两直角三角形向内折叠，如图2，若a＝4，b＝6，求此时空白部分的面积；

(3)、如图3，将八个全等的直角三角形紧密地拼接，记图中正方形ABCD，正方形EFGH、正方形MNKT的面积分别为S₁ ， S₂ ， S₃ ．若S₁+S₂+S₃＝40，求S₂的值．

查看试题解析