河北省唐山市路北区2020-2021学年八年级下学期期中数学试题
试卷更新日期:2022-03-15 类型:期中考试
一、单选题
-
1. 使二次根式 有意义的x的取值范围是( )A、x≠2 B、x>2 C、x≤2 D、x≥22. 下列根式中,不是最简二次根式的是( )A、 B、x C、 D、3. 下列四组数据中,不能作为直角三角形三边长的是( )A、5,12,13 B、1,2,3 C、9,40,41 D、3,4,54. 下列说法不正确的是( )A、中,若 , 则是直角三角形 B、中,若 , 则是直角三角形 C、的三边之比是5:12:13,则是直角三角形 D、中,若 , 则不是直角三角形5. 已知 是整数,则正整数n的最小值是( )A、4 B、6 C、8 D、126. 一次函数y=x+2的图象与y轴的交点坐标为( )A、(0,2) B、(0,-2) C、(2,0) D、(-2,0)7. 将直线 向右平移2个单位,再向上平移3个单位后,所得的直线的表达式为( )A、 B、 C、 D、8. 如图,数轴上有A、B、C、D四个点,下列说法正确的是( )
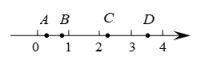 A、点A表示的数约为 B、点B表示的数约为 C、点C表示的数约为 D、点D表示的数约为9. 若1<x<2,则 的值为( )A、2x-4 B、-2 C、4-2x D、210. 如图,数轴上点A对应的数是0,点B对应的数是1, , 垂足为B,且BC=1,以A为圆心,为半径画弧,交数轴于点D,则点D表示的数为( )
A、点A表示的数约为 B、点B表示的数约为 C、点C表示的数约为 D、点D表示的数约为9. 若1<x<2,则 的值为( )A、2x-4 B、-2 C、4-2x D、210. 如图,数轴上点A对应的数是0,点B对应的数是1, , 垂足为B,且BC=1,以A为圆心,为半径画弧,交数轴于点D,则点D表示的数为( )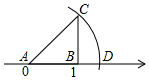 A、 B、 C、 D、11. 一次函数y=kx+3(k≠0)的函数值y随x的增大而增大,它的图象不经过的象限是( )A、第一 B、第二 C、第三 D、第四12.
A、 B、 C、 D、11. 一次函数y=kx+3(k≠0)的函数值y随x的增大而增大,它的图象不经过的象限是( )A、第一 B、第二 C、第三 D、第四12.若函数y=kx﹣b的图象如图所示,则关于x的不等式k(x﹣3)﹣b>0的解集为( )
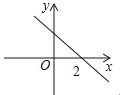 A、x<2 B、x>2 C、x<5 D、x>513. 若以二元一次方程x+2y﹣b=0的解为坐标的点(x,y)都在直线y=﹣ x+b﹣1上,则常数b=( )A、 B、2 C、﹣1 D、114. 若式子 有意义,则一次函数 的图象可能是( )A、
A、x<2 B、x>2 C、x<5 D、x>513. 若以二元一次方程x+2y﹣b=0的解为坐标的点(x,y)都在直线y=﹣ x+b﹣1上,则常数b=( )A、 B、2 C、﹣1 D、114. 若式子 有意义,则一次函数 的图象可能是( )A、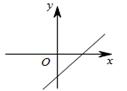 B、
B、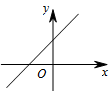 C、
C、 D、
D、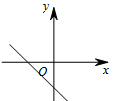
二、填空题
-
15. 化简= .16. 在正比例函数y=﹣3mx中,函数y的值随x值的增大而增大,则P(m,5)在第象限.17. 如图所示,一次函数y=ax+b的图象与x轴相交于点(2,0),与y轴相交于点(0,4),结合图象可知,关于x的方程ax+b=0的解是 .
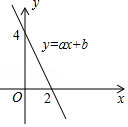 18. 如图,一只蚂蚁沿长方体的表面从顶点A爬到另一顶点M,已知AB=AD=2,BF=3.这只蚂蚁爬行的最短距离 .
18. 如图,一只蚂蚁沿长方体的表面从顶点A爬到另一顶点M,已知AB=AD=2,BF=3.这只蚂蚁爬行的最短距离 .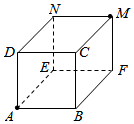
三、解答题
-
19. 计算:(1)、(2)、 .20. 已知y与x-1成正比例,并且当x=3时,y=-4.(1)、求y与x之间的函数关系式;(2)、如果函数图象经过点P(m,6),求m的值.21. 某学校积极响应怀化市“三城同创”的号召,绿化校园,计划购进A,B两种树苗,共21棵,已知A种树苗每棵90元,B种树苗每棵70元.设购买A种树苗x棵,购买两种树苗所需费用为y元.(1)、求y与x的函数表达式,其中0≤x≤21;(2)、若购买B种树苗的数量少于A种树苗的数量,请给出一种费用最省的方案,并求出该方案所需费用.22. 如图所示有一张图纸被损坏,上面两个标志点 , 清晰,而主要建筑标志点)破损.
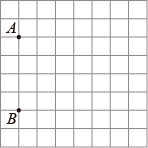 (1)、请建立直角坐标系并确定图中C点的位置;(2)、是否为直角三角形?请证明.23. 如图,在平面直角坐标系中,直线 过点 且与 轴交于点 ,把点 向左平移2个单位,再向上平移4个单位,得到点 .过点 且与 平行的直线交 轴于点 .
(1)、请建立直角坐标系并确定图中C点的位置;(2)、是否为直角三角形?请证明.23. 如图,在平面直角坐标系中,直线 过点 且与 轴交于点 ,把点 向左平移2个单位,再向上平移4个单位,得到点 .过点 且与 平行的直线交 轴于点 . (1)、求直线 的解析式;
(1)、求直线 的解析式;
(2)、直线 与 交于点 ,将直线 沿 方向平移,平移到经过点 的位置结束,求直线 在平移过程中与 轴交点的横坐标的取值范围.
24. 求代数式 的值,其中a=﹣2020如图是小亮和小芳的解答过程.
小亮:解:原式=
小芳:解:原式=
(1)、的解法是不正确的;(2)、不正确的原因在于未能正确地运用二次根式的性质:;(3)、求代数式 的值,其中a=﹣2019.25. 一艘轮船从A港向南偏西48°方向航行100km到达B岛,再从B岛沿BM方向航行125km到达C岛,A港到航线BM的最短距离是60km. (1)、若轮船速度为25km/小时,求轮船从C岛沿CA返回A港所需的时间.(2)、C岛在A港的什么方向?26. 如图,已知函数y=mx 的图象为直线l1 , 函数y=kx+b的图象为直线l2 , 直线l1、l2分别交x轴于点B和点C(3,0),分别交y轴于点D和E,l1和l2相交于点A(2,2).
(1)、若轮船速度为25km/小时,求轮船从C岛沿CA返回A港所需的时间.(2)、C岛在A港的什么方向?26. 如图,已知函数y=mx 的图象为直线l1 , 函数y=kx+b的图象为直线l2 , 直线l1、l2分别交x轴于点B和点C(3,0),分别交y轴于点D和E,l1和l2相交于点A(2,2).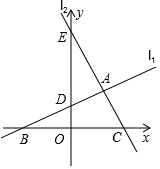 (1)、填空:m=;求直线l2的解析式为;(2)、若点M是x轴上一点,连接AM,当△ABM的面积是△ACM面积的2倍时,请求出符合条件的点M的坐标;(3)、若函数y=nx﹣6的图象是直线l3 , 且l1、l2、l3不能围成三角形,直接写出n的值.
(1)、填空:m=;求直线l2的解析式为;(2)、若点M是x轴上一点,连接AM,当△ABM的面积是△ACM面积的2倍时,请求出符合条件的点M的坐标;(3)、若函数y=nx﹣6的图象是直线l3 , 且l1、l2、l3不能围成三角形,直接写出n的值.