河北省秦皇岛市青龙县2020-2021学年八年级下学期期中考试数学试题

试卷更新日期：2022-03-15 类型：期中考试

进入 出卷网 下载

一、单选题

  • 1. 下列调查中，调查方式选择合理的是（　　）
    A、节能灯厂要检测一批节能灯的使用寿命，采用全面调查方式 B、调查某一品牌5万袋包装鲜奶是否符合卫生标准，采用抽样调查方式 C、了解秦皇岛市城区居民日平均用水量，采用全面调查方式 D、旅客上飞机前的安检，采用抽样调查方式

    查看试题解析

  • 2. 今年我县有3900名考生参加中考，为了了解这些考生的数学成绩，从中抽取200名考生的数学成绩进行统计分析，在这个问题中，下列说法正确的是（     ）
    A、3900名考生的中考成绩的全体是总体 B、每个考生是个体 C、200名考生是总体的一个样本 D、样本的容量是200

    查看试题解析

  • 3. 下列数据能确定物体具体位置的是（　　）
    A、东经118°，北纬28° B、希望路右边 C、北偏东30° D、明华小区4号楼

    查看试题解析

  • 4. 点P(2，－5)所在的象限是（     ）
    A、第一象限 B、第二象限 C、第三象限 D、第四象限

    查看试题解析

  • 5. 甲以每小时20km的速度行驶时，他所走的路程S（km）与时间t（h）之间可用公式s＝20t来表示，则下列说法正确的是（   ）
    A、数20和s，t都是变量 B、s是常量，数20和t是变量 C、数20是常量，s和t是变量 D、t是常量，数20和s是变量

    查看试题解析

  • 6. 在方格纸上画出的小旗图案如图所示，若用(﹣2，1)表示A点，(﹣2，5)表示B点，那么C点的位置可表示为（    ）

    A、(3，5) B、(5，3) C、(1，3) D、(1，2)

    查看试题解析

  • 7. 函数y=1x−1自变量的取值范围是（       ）．
    A、x≥1 B、x<1 C、x≠1 D、x>−1

    查看试题解析

  • 8. 在平面直角坐标系中，将三角形三个顶点的横坐标都增加3，纵坐标保持不变，所得的新图形与原图形相比（     ）
    A、向上平移了3个单位长度 B、向下平移了3个单位长度 C、向左平移了3个单位长度 D、向右平移了3个单位长度

    查看试题解析

  • 9. 过A(4，－3)和B(－4，－3)两点的直线一定（       ）
    A、垂直于x轴 B、与x轴相交但不垂直 C、平行于x轴 D、平行于y轴

    查看试题解析

  • 10. 据不完全统计，2020年1--4月份我国某型号新能源客车的月销量情况如图所示，下列说法不正确的是（     ）

    A、1月份销量为2万辆 B、从2月到3月的月销量增长最快 C、4月份销量比3月份增加了0.9万辆 D、1~4月新能源客车销量逐月增加

    查看试题解析

  • 11. 已知点P在第四象限，且到x轴的距离为2，到y轴距离是4，则点P的坐标为（       ）
    A、(4 ， −2) B、(−4 ， 2) C、(−2 ， 4) D、(2 ， −4)

    查看试题解析

  • 12. 如图，动点P在平面直角坐标系中按图中箭头所示方向运动，第1次从原点运动到点(1，1)，第2次接着运动到点（2，0），第3次接着运动到点（3，2），…，按这样的运动规律，经过第2021次运动后，动点P的坐标是（       ）

    A、（2020， 0） B、（2021，1） C、（2021，2） D、（2021，0）

    查看试题解析

二、填空题

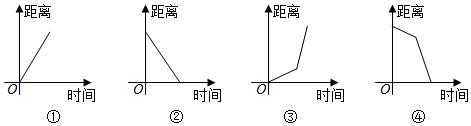
  • 13. 若电影票上座位是12排5号可记为（12，5），则（5，6）表示 ．

    查看试题解析

  • 14. 点A(−1 ， 2)关于x轴对称点的坐标是  ．

    查看试题解析

  • 15. 函数y= x –1的自变量x的取值范围是.

    查看试题解析

  • 16. 为了了解某地区45000名九年级学生的睡眠情况，运用所学统计知识解决上述问题所要经历的几个主要步骤：①抽样调查；②设计调查问卷；③用样本估计总体；④分析、整理数据；按操作的先后进行排序为 ． （只写序号）

    查看试题解析

  • 17. 小明早上步行去车站，然后坐车去学校．如图象中，能近似的刻画小明离学校的距离随时间变化关系的图象是 ． （填序号）

    查看试题解析

  • 18. 根据如图所示的程序计算函数y的值，若输入x的值是7，则输出y的值是.

    查看试题解析

三、解答题

  • 19. 如图，这是某市部分简图，请以火车站为坐标原点向东的方向为 x 轴的正方向，建立平面直角坐标系，并分别写出火车站以北（包括火车站）各地点的坐标．（每个正方形边长是 1）

    查看试题解析

  • 20. 为了传承中华民族优秀传统文化，石家庄市某中学组织了一次“中华民族优秀传统文化知识竞赛”活动，比赛后整理参赛学生的成绩，将参赛学生的成绩分为A、B、C、D四个等级，并制作了如下的统计表和统计图，但都不完整，请你根据统计图、表解答下列问题：

       

    等级

    频数（人）

    频率

    A

    30

    10%

    B

    90

    30%

    C

    m

    40%

    D

    60

    n

    (1)、在表中，m＝　                  　；n＝　                        　；
    (2)、补全频数直方图；
    (3)、扇形统计图中圆心角β的度数是；
    (4)、请你估计全市八年级2万名考生中，成绩评为“B”级及以上的学生大约有多少名？

    查看试题解析

  • 21. 如图所示的正方形网格中，每个小正方形的边长均为1，△ABC的三个顶点均为格点。若点C的坐标为(−1 ， 3) ， 按要求回答下列问题：

    (1)、在图中建立正确的平面直角坐标系，写出点A和点B的坐标；
    (2)、画出△ABC关于x轴对称的△A1B1C1.

    查看试题解析

  • 22. 在一定限度内弹簧挂上物体后会伸长，测得一弹簧长度y(cm)与所挂物体质量x(kg有如下关系：(假设都在弹性限度内)

    所挂物体质量x/kg

    0

    1

    2

    3

    4

    5

    弹簧长度y/cm

    12

    12.5

    13

    13.5

    14

    14.5

    (1)、由表格知，弹簧原长为cm，所挂物体每增加1kg弹簧伸长cm．
    (2)、请写出弹簧长度y(cm)与所挂物体质量x(kg)之间的关系式．
    (3)、预测当所挂物体质量为10kg时，弹簧长度是多少？
    (4)、当弹簧长度为20cm时，求所挂物体的质量．

    查看试题解析

  • 23. 如图，已知长方形ABCO中，边AB=12，BC=8．以点O为原点，OA、OC所在的直线为y轴和x轴建立直角坐标系．

    (1)、点A的坐标为（0，8），写出B、C两点的坐标；
    (2)、若点P从C点出发，以3单位/秒的速度向CO方向移动（不超过点O），点Q从原点O出发，以2单位/秒的速度向OA方向移动（不超过点A），设P、Q两点同时出发，t秒后，写出△BCP的面积S与t之间的函数关系式；
    (3)、在P、Q移动过程中，四边形OPBQ的面积是否发生变化?若不变，求其值；若变化，求变化范围．

    查看试题解析

  • 24. “龟兔赛跑”的故事同学们都非常熟悉，图中的线段OD和折线OABC表示“龟兔赛跑”时路程与时间的关系，请你根据图中给出的信息，解决下列问题．

    (1)、线段OD表示赛跑过程中的路程与时间的关系（填“乌龟”和“兔子”）．赛跑的全程是米．
    (2)、兔子在起初每分钟跑米，乌龟每分钟爬米．
    (3)、兔子醒来，以750米/分的速度跑向终点，结果还是比乌龟晚到了1分钟，请你算算兔子中间停下睡觉用了多少分钟？

    查看试题解析