山西省晋中市祁县2020-2021学年九年级下学期期中数学试题

试卷更新日期：2022-03-15 类型：期中考试

进入出卷网下载

一、单选题

1. 计算 $- 4 \times (- 2)$ 的结果是（）

A、-8 B、8 C、-6 D、6

查看试题解析
2. 下列运算不正确的是（）

A、 ${(- \frac{3}{2})}^{0} = 1$ B、 $3 \sqrt{2} - \sqrt{8} = \sqrt{2}$ C、 $4 x^{3} \div 2 x = 2 x^{2}$ D、 $(a + b) (a - b) = 2 a b$

查看试题解析
3. 如图，直线 $c ， d$ 分别与直线 $a ， b$ 相交， $∠ 3 + ∠ 4 = 18 0^{°}$ ，若 $∠ 1 = 10 0^{°}$ ，则 $∠ 2$ 的度数为（）

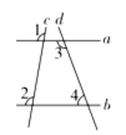A、80° B、90° C、100° D、110°

查看试题解析
4. 某学校举行了“重视阅读教学，提高核心素养”系列活动，在增大课堂阅读的同时还鼓励同学进行大量的课后阅读.王老师调查了上个月全班学生阅读课外图书的本数，统计结果如下表所示，则在本次调查中，全班学生阅读课外图书本数的平均数和众数分别是（）
阅读课外图书的本数（本）
0
1
2
3
人数
2
18
14
6

A、1.6，1 B、1，1.5 C、1.6，1.5 D、1，1

查看试题解析
5. 化简 $\frac{1}{1 - a} + \frac{2 a}{a^{2} - 1}$ 的结果是（）

A、 $a - 1$ B、 $1 - a$ C、 $\frac{1}{a - 1}$ D、 $\frac{1}{1 + a}$

查看试题解析
6. 若关于 $x$ 的一元二次方程 $x^{2} - 2 x + \frac{1}{2} m + 3 = 0$ 有两个相等的实数根，则 $m$ 的值是（）

A、-8 B、-4 C、-2 D、2

查看试题解析
7. 某广场有一个小型喷泉，水流从垂直于地面的水管 $O A$ 喷出， $O A$ 长为 $1.5 m$ .水流在各个方向上沿形状相同的抛物线路径落到地面上，某方向上抛物线路径的形状如图所示，落点B到O的距离为 $3 m$ .建立平面直角坐标系，水流喷出的高度 $y (m)$ 与水平距离 $x (m)$ 之间近似满足函数关系 $y = a x^{2} + x + c (a \neq 0)$ ，则水流喷出的最大高度为（）

A、 $1 m$ B、 $\frac{3}{2} m$ C、 $\frac{13}{8} m$ D、 $2 m$

查看试题解析
8. 勾股定理是人类早期发现并证明的重要数学定理之一，是用代数思想解决几何问题的最重要的工具之一，它也是数学定理中证明方法最多的定理之一.美国第20任总统詹姆斯·加菲尔德的证法如下：
$∵ S_{梯形 A B C D} = \frac{1}{2} (a + b)^{2} = \frac{1}{2} (a^{2} + 2 a b + b^{2})$ ， ${S_{梯形 A B C D}}_{} = S_{Δ A B D} + S_{Δ E B C} + S_{Δ C E D} = \frac{1}{2} a b$ $+ \frac{1}{2} b a + \frac{1}{2} c^{2} = \frac{1}{2} (2 a b + c^{2}) ， ∴$ 比较上二式可得 $c^{2} = a^{2} + b^{2}$ .
此证明方法体现的数学思想是（）

A、整体思想 B、转化思想 C、数形结合思想 D、分类讨论思想

查看试题解析
9. 如图，在 $⊙ O$ 中， $O A ⊥ O B ， C D = D E = \sqrt{2} ， ∠ C D E = 9 0^{°}$ ，则图中阴影部分的面积为（）

A、 $\frac{π}{4} - \frac{1}{2}$ B、 $\frac{π}{4}$ C、 $\frac{π}{2} - \frac{1}{2}$ D、 $\frac{π}{2} - 1$

查看试题解析

二、填空题

10. 将二次函数 $y = (x + 1)^{2} - 1$ 的图象先向右平移1个单位长度，再向上平移2个单位长度，所得的二次函数的解析式为.

查看试题解析
11. 在一个不透明盒子中放入四张卡片，四张卡片上分别写有数字 $- 2 ， - 1 ， 0 ， 1$ ，每张卡片除数字不同外其他都相同从中随机抽取两张卡片，其数字之和为非负数的概率是.

查看试题解析
12. 如图，在 $△ A B C$ 中，若 $∠ C = 90 °$ ，利用直尺和圆规按照以下步骤作图：①以点 $A$ 为圆心，任意长为半径作弧，分别交 $∠ B A C$ 的两边于点 $D 、 E$ ；②分别以点 $D 、 E$ 为圆心，大于 $\frac{1}{2} D E$ 为半径作弧，两弧相交于点 $M$ ；③作射线 $A M$ 交 $B C$ 于点 $F$ ，以点 $A$ 为圆心， $A F$ 为半径作弧，交线段 $A B$ 于点 $H$ .若 $∠ B = 26 °$ ，则 $∠ H F A =$ .

查看试题解析
13. 如图，是由白色正方形和灰色等腰直角三角形按照一定规律摆成的图形，按此规律，则第 $n$ 个图形中共有灰色等腰直角三角形个（用含 $n$ 的代数式表示）

查看试题解析
14. 如图，四边形ABCD是一张矩形纸片，AB＝4，点G是CD的中点，先将矩形纸片ABCD沿过点B的直线折叠，使点A落在BC上的点F处，折痕为BE，然后把纸片展平．再将矩形纸片ABCD沿BG折叠，点C恰好落在BE上的点H处，折痕为BG，然后再把纸片展平，分别连接EF、HG，BG，则BC的长为．

查看试题解析

三、解答题

15.

(1)、计算： ${(- \frac{1}{2})}^{- 1} + t a n 45 °$ $+ 202 1^{0} - | 1 - \sqrt{2} |$

(2)、阅读下面的计算过程，并回答下面的问题：
解方程组： ${\begin{array}{l} 4 x + 3 y = 5 ① \\ x - 2 y = 4 ② \end{array}$

解：②×4，得 4x－2y＝16 ③ ．．．．．．第一步

①－③，得5y＝－11．．．．．．第二步

解得y＝ $- \frac{11}{5}$ ．．．．．．第三步

把y＝ $- \frac{11}{5}$ 代入②，得x＝ $- \frac{2}{5}$ ．．．．．．第四步

∴原方程组的解为 ${\begin{array}{l} x = - \frac{2}{5} \\ y = - \frac{11}{5} \end{array}$ ．．．．．．第五步

①以上解题过程中，第二步变形实现了的目的，体现了的数学思想；

②第步开始出现错误，这一步不正确的原因是；

③请写出正确的解题过程．

查看试题解析
16. 如图，在△ABC中，AC＝10cm，D为边AB上一点，且AD＝2BD．

(1)、实践操作：利用尺规按下列要求作图，并在图中标明相应的字母（保留作图痕迹，不写作法）过点D作DE∥BC，交AC边于点E

(2)、求AE的长．

查看试题解析
17. 中华文化博大精深，有着深厚的底蕴，学习传统文化有利于我们的发展改革．电视是一个传播传统文化很好地平台，《中国诗词大会》是中央电视台首档全民参与的诗词节目，节目以“赏中华诗词、寻文化基因、品生活之美”为基本宗旨，带动全民重温那些曾经学过的古诗词，分享诗词之美，感受诗词之趣，从古人的智慧和情怀中汲取营养，涵养心灵．节目自从开播以来，成为网络热搜．为此，国内知名搜索引擎，基于广大网民的搜索行为，对关注《中国诗词大会》节目的人群特征作了数据调查．根据搜索大数据绘制了如下统计图表．

年龄段
＜19
19－24
25－34
35－49
≥50
偏好指数
1.9
____
1.025
0.8
____
请根据统计图表解答下列问题：

(1)、在扇形统计图中，35－49岁年龄段人数所占的百分比是，此年龄段人数对应的扇形的圆心角是度．

(2)、补全条形统计图和偏好指数统计表．

(3)、根据统计图表的信息，谈谈你对关注《中国诗词大会》节目的人群特征的认识．

查看试题解析
18. 如图，在平面直角坐标系中，一次函数y＝2x＋2的图象与x轴、y轴分别交于点A、B，与反比例函数 $y = \frac{k}{x}$ 的图象交于点C（1，m），过点B作y轴的垂线交反比例函数 $y = \frac{k}{x}$ 的图象于点D，连接AD，求k的值及△ABD的面积．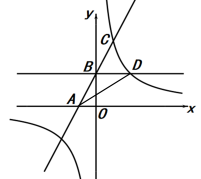

查看试题解析
19. 大数据时代的降临带来了大量爆炸性的知识增长，其中很大一部分被转化为实用技术推入商用，激光电视就是近几年发展相当迅猛的其中一支．激光电视最值得一提的是对消费者眼睛的保护方面，其光源是激光，运用了反射成像原理，屏幕不通电，无辐射，观看时不会感到刺眼．根据THX、isf观影标准，水平视角33－40°时，双眼处于肌肉放松状态，是享受震撼感官体验的客厅黄金观影位．

(1)、如图，小佳家决定要换一个激光电视，他家客厅的观影距离（人坐在沙发上眼睛到屏幕的距离）为3.5米，请你计算一下小佳家要选择电视屏幕宽（BC的长）在什么范围内的激光电视就能享受黄金观看体验？（结果精确到0.1m，参考数据：sin33°≈0.54，cos33°≈0.84，tan33°≈0.65，sin40°≈0.64，cos40°≈0.77，tan40°≈0.84，sin16.5°≈0.28，cos16.5°≈0.96，tan16.5°≈0.30，sin20°≈0.34，cos20°≈0.94，tan20°≈0.36）

(2)、由于技术革新，激光电视的功能越来越强大，价格也逐渐下降，某电器行经营的某款激光电视去年销售总额为50万元，今年每台销售价比去年降低4000元，若卖出的数量相同，销售总额将比去年减少20%，今年这款激光电视每台的售价是多少元？

查看试题解析
20. 阅读下列材料，并完成相应的任务：阿基米德是古希腊最伟大的数学家之一，他流传于世的数学著作有十余种．下面是《阿基米德全集》的《引理集》中记载的一个命题：如图1，AB是⊙O的弦，C在⊙O上，CD⊥AB于点D，在弦AB上取一点E，使AD＝DE，点F是弧BC上的一点，且 $\overset{⌢}{C F} = \overset{⌢}{C A}$ ，连接BF，则BF＝BE．
小颖思考后，给出了如下证明：
如图2，连接AC、CE、CF、EF
∵CD⊥AB，AD＝DE
∴AC＝CE（依据1）
∴∠A＝∠CEA
∵ $\overset{⌢}{C F} = \overset{⌢}{C A}$
∴CF＝AC（依据2）
∴CF＝CE
∴∠CEF＝∠CFE
任务：

(1)、依据1：；依据2：；

(2)、请按照上面的证明思路，完成该命题证明的剩余部分；

(3)、如图3，将图2中的“弦AB”改为“直径AB”，作直线 $l$ 与⊙O相切于点F，过点B作BG⊥ $l$ 于点G，其余条件不变．若AB＝10，AD＝2，则线段FG的长为．

查看试题解析
21. 如图

(1)、如图①，在等边三角形ABC中，点P在△ABC内，且∠APB＝150°，猜想PA，PB，PC三条线段之间有何数量关系，并说明理由．
小明同学通过观察、分析、思考，对上述问题形成了如下想法：
想法一：将△APC绕点A按顺时针方向旋转60°，得到△AP′B，连接PP′，寻找PA，PB，PC三条线段之间的数量关系；
想法二：将△APB绕点A按逆时针方向旋转60°，得到△AP′C，连接PP′，寻找PA，PB，PC三条线段之间的数量关系．…
请参考小明同学的想法，补充图形，并完成该问题的解答过程．（一种方法即可）

(2)、如图②，点P是正方形ABCD内一点，若∠APB＝135°，PA，PB，PC三条线段之间又有何数量关系？请说明理由．

(3)、如图③，点P是正方形ABCD外一点，若PA，PB，PC三条线段满足“类比探究”中的数量关系，请直接写出∠APB的度数．

查看试题解析
22. 如图，抛物线 $y = \frac{1}{2} x^{2} - 2 x - 6$ 与 $x$ 轴交于 $A$ 、 $B$ 两点，与 $y$ 轴交于点 $C$ ，点 $P$ 是线段 $O B$ 上的一个动点（不与 $O$ 、 $B$ 重合），过点 $P$ 作直线 $P D ⊥ x$ 轴交抛物线于点 $D$ ，交直线 $B C$ 于点 $E$ ．

(1)、求 $A$ 、 $B$ 两点的坐标，及直线 $B C$ 的表达式；

(2)、若 $D E = 2 P E$ 时，求线段 $D E$ 的长；

(3)、在（2）的条件下，若点 $Q$ 是直线 $P D$ 上的一个动点，点 $M$ 是抛物线上的一个动点，是否存在以 $B$ 、 $C$ 、 $Q$ 、 $M$ 为顶点的四边形是平行四边形？若存在，请直接写出点 $Q$ 的坐标；若不存在，请说明理由．

查看试题解析

年龄段	＜19	19－24	25－34	35－49	≥50
偏好指数	1.9	____	1.025	0.8	____

阅读课外图书的本数（本）	0	1	2	3
人数	2	18	14	6