内蒙古自治区赤峰市松山区2020-2021学年九年级下学期期中数学试题
试卷更新日期:2022-03-15 类型:期中考试
一、单选题
-
1. 的算术平方根是( )A、4 B、﹣4 C、2 D、﹣22. 如图图形中,是中心对称图形的是( )A、
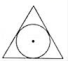 B、
B、 C、
C、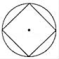 D、
D、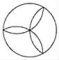 3. 下列运算正确的是( )A、a2+a2=2a4 B、a2•a3=a6 C、(a3)2=a6 D、(2a2)3=6a64. 达里诺尔湖又称达理湖,汉语译为“大海一样的湖”.是内蒙古地区四大名湖之一,内蒙古赤峰市最大的湖泊,位于内蒙古赤峰市克什克腾旗高原地区,分布着被风化的玄武岩或花岗岩,是低浓度盐水湖,达里诺尔湖湖,周长百余公里,呈海马状,为封闭式苏达型半咸水湖,达里诺尔湖属高原内陆湖,湖水无外泻,总储水量达16亿立方米,16亿用科学记数法表示为( )A、16×108 B、1.6×108 C、1.6×109 D、1.6×10105. 赤峰市某青少年宫门前有一座正方体雕塑,它的每个面上都有一个汉字,如图是该正方体模型的展开图,那么在正方体中,与“英”字所在面相对的面上的汉字是( )
3. 下列运算正确的是( )A、a2+a2=2a4 B、a2•a3=a6 C、(a3)2=a6 D、(2a2)3=6a64. 达里诺尔湖又称达理湖,汉语译为“大海一样的湖”.是内蒙古地区四大名湖之一,内蒙古赤峰市最大的湖泊,位于内蒙古赤峰市克什克腾旗高原地区,分布着被风化的玄武岩或花岗岩,是低浓度盐水湖,达里诺尔湖湖,周长百余公里,呈海马状,为封闭式苏达型半咸水湖,达里诺尔湖属高原内陆湖,湖水无外泻,总储水量达16亿立方米,16亿用科学记数法表示为( )A、16×108 B、1.6×108 C、1.6×109 D、1.6×10105. 赤峰市某青少年宫门前有一座正方体雕塑,它的每个面上都有一个汉字,如图是该正方体模型的展开图,那么在正方体中,与“英”字所在面相对的面上的汉字是( )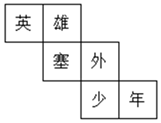 A、塞 B、外 C、少 D、年6. 有一天,兔子和乌龟赛跑.比赛开始后,兔子飞快地奔跑,乌龟缓慢的爬行.不一会儿,乌龟就被远远的甩在了后面.兔子想:“这比赛也太轻松了,不如先睡一会儿.”而乌龟一刻不停地继续爬行.当兔子醒来跑到终点时,发现乌龟已经到达了终点.符合题意反映这则寓言故事的大致图象是( )
A、塞 B、外 C、少 D、年6. 有一天,兔子和乌龟赛跑.比赛开始后,兔子飞快地奔跑,乌龟缓慢的爬行.不一会儿,乌龟就被远远的甩在了后面.兔子想:“这比赛也太轻松了,不如先睡一会儿.”而乌龟一刻不停地继续爬行.当兔子醒来跑到终点时,发现乌龟已经到达了终点.符合题意反映这则寓言故事的大致图象是( )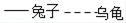 A、
A、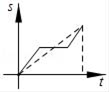 B、
B、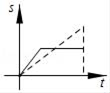 C、
C、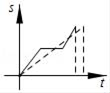 D、
D、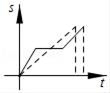 7. 不等式组的解集是( )A、x<3 B、x>3 C、x<4 D、x>48. 如图,AB∥CD,E为CD上一点,射线EF经过点A,EC=EA.若∠CAE=30°,则∠BAF=( )
7. 不等式组的解集是( )A、x<3 B、x>3 C、x<4 D、x>48. 如图,AB∥CD,E为CD上一点,射线EF经过点A,EC=EA.若∠CAE=30°,则∠BAF=( ) A、30° B、40° C、50° D、60°9. 汉代数学家赵爽在注解《周髀算经》时给出的“赵爽弦图”是我国古代数学的瑰宝,如图所示的弦图中,四个直角三角形都是全等的,他们的两条直角边之比均为2:3,现随机向该图形内掷一枚小针,则针尖落在阴影区域的概率为( )
A、30° B、40° C、50° D、60°9. 汉代数学家赵爽在注解《周髀算经》时给出的“赵爽弦图”是我国古代数学的瑰宝,如图所示的弦图中,四个直角三角形都是全等的,他们的两条直角边之比均为2:3,现随机向该图形内掷一枚小针,则针尖落在阴影区域的概率为( )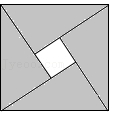 A、 B、 C、 D、10. 程大位《直指算法统宗》趣题:“一百馒头一百僧,大僧三个更无争,小僧三人分一个,大小和尚各几丁?”意思是:有100个和尚分100个馒头,如果大和尚1人分3个,小和尚3人分1个,正好分完,试问大、小和尚各多少人?设小和尚有x人,依题意列方程得( )A、 B、 C、 D、11. 如图,已知⊙O的直径AE=10cm,∠B=∠EAC,则AC的长为( )
A、 B、 C、 D、10. 程大位《直指算法统宗》趣题:“一百馒头一百僧,大僧三个更无争,小僧三人分一个,大小和尚各几丁?”意思是:有100个和尚分100个馒头,如果大和尚1人分3个,小和尚3人分1个,正好分完,试问大、小和尚各多少人?设小和尚有x人,依题意列方程得( )A、 B、 C、 D、11. 如图,已知⊙O的直径AE=10cm,∠B=∠EAC,则AC的长为( )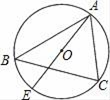 A、5cm B、5 cm C、5 cm D、6cm12. 如图,一段公路的转弯处是一段圆弧AB,则扇形AOB的面积为( )
A、5cm B、5 cm C、5 cm D、6cm12. 如图,一段公路的转弯处是一段圆弧AB,则扇形AOB的面积为( )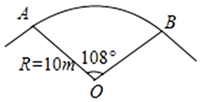 A、15πm2 B、30πm2 C、18πm2 D、12πm213. 下列调查方式中最适合的是( )A、要了解一批节能灯的使用寿命,采用全面调查方式 B、调查你所在班级的同学的身高,采用抽样调查方式 C、环保部门调查老哈河某段水域的水质情况,采用抽样调查方式 D、调查全市中学生每天的就寝时间,采用全面调查方式14. 如图,在平面直角坐标系中,过点O的⊙O 1与两坐标轴分别交于A、B两点,A(5,0),B(0,3),点C在弧OA上,则tan∠BCO=( )
A、15πm2 B、30πm2 C、18πm2 D、12πm213. 下列调查方式中最适合的是( )A、要了解一批节能灯的使用寿命,采用全面调查方式 B、调查你所在班级的同学的身高,采用抽样调查方式 C、环保部门调查老哈河某段水域的水质情况,采用抽样调查方式 D、调查全市中学生每天的就寝时间,采用全面调查方式14. 如图,在平面直角坐标系中,过点O的⊙O 1与两坐标轴分别交于A、B两点,A(5,0),B(0,3),点C在弧OA上,则tan∠BCO=( )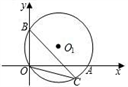 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
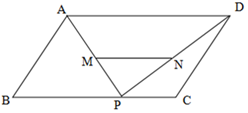
15. 分解因式8m﹣8﹣2m2= .16. 已知反比例函数 的图像在第二、四象限,点(﹣ , y1),(﹣ , y2),( , y3)是这个函数图象上的点,则将y1、y2、y3按从小到大排列为 .17. 如图,P是平行四边形ABCD边BC上的一点,M、N分别是PA、PD的中点,若△PMN的面积为3cm2 , 则平行四边形ABCD的面积是cm2 .
 18. 已知有理数a≠1,我们把称为a的差倒数,如2的差倒数是=﹣1,﹣1的差倒数是 , 如果a1=﹣2,a2是a1的差倒数,a3是a2的差倒数,a4是a3的差倒数……以此类推,a2021的值是 .
18. 已知有理数a≠1,我们把称为a的差倒数,如2的差倒数是=﹣1,﹣1的差倒数是 , 如果a1=﹣2,a2是a1的差倒数,a3是a2的差倒数,a4是a3的差倒数……以此类推,a2021的值是 .三、解答题
-
19. 计算:6cos45°+()﹣1+(﹣1.73)0+|5﹣3|+42021×(﹣0.25)2021 .20. 如图,在Rt△ABC中,∠C=90°,AC=6,BC=8.
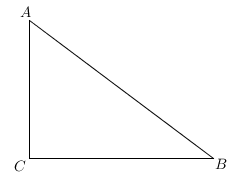 (1)、尺规作图:作三角形ABC的内切圆⊙O,⊙O分别与AB、BC、CA相切于点D、E、F保留作图痕迹,不写作法.(2)、求⊙O的半径r.21. 2015年7月31日,托马斯巴赫宣布2022年冬季奥林匹克运动会主办城市是北京,北京成为第一个举办过夏季奥林匹克运动会和冬季奥林匹克运动会以及亚洲运动会三项国际赛事的城市,也是继1952年挪威的奥斯陆举办后时隔70年的第二个举办冬奥会的首都城市,北京冬季奥运会设7个大项,15个分项,109个小项.北京将主办冰上项目,张家口将主办雪上项目,延庆协办张家口举办雪上项目,其中在北京举办的冰上项目共分为A.短道速滑、B.速度滑冰、C.花样滑冰、D.冰球、E冰壶五个小项.体育老师针对某个班级的学生喜欢哪个项目比赛做了调查,并将调查结果制成如下两幅不充整的统计图:
(1)、尺规作图:作三角形ABC的内切圆⊙O,⊙O分别与AB、BC、CA相切于点D、E、F保留作图痕迹,不写作法.(2)、求⊙O的半径r.21. 2015年7月31日,托马斯巴赫宣布2022年冬季奥林匹克运动会主办城市是北京,北京成为第一个举办过夏季奥林匹克运动会和冬季奥林匹克运动会以及亚洲运动会三项国际赛事的城市,也是继1952年挪威的奥斯陆举办后时隔70年的第二个举办冬奥会的首都城市,北京冬季奥运会设7个大项,15个分项,109个小项.北京将主办冰上项目,张家口将主办雪上项目,延庆协办张家口举办雪上项目,其中在北京举办的冰上项目共分为A.短道速滑、B.速度滑冰、C.花样滑冰、D.冰球、E冰壶五个小项.体育老师针对某个班级的学生喜欢哪个项目比赛做了调查,并将调查结果制成如下两幅不充整的统计图:
根据统计图提供的信息,解答下列问题:
(1)、本次共调查了名学生;(2)、请根据以上信息,补全条形统计图;(3)、扇形统计图中的m的值是 , 类别D所对应的扇形圆心角的度数是度.(4)、若该校有800名学生,根据抽样调查的结果,请你估计该校有多少名学生喜欢速度滑冰?22. 某公司开发了一种新产品,现要在甲地或者乙地进行销售,设年销售量为x(件),其中x>0.若在甲地销售,每件售价y(元)与x之间的函数关系式为y=﹣x+100,每件成本为20元,设此时的年销售利润为w甲(元)(利润=销售额﹣成本).
若在乙地销售,受各种不确定因素的影响,每件成本为a元(a为常数,18≤a≤25),每件售价为98元,销售x(件)每年还需缴纳x2元的附加费.设此时的年销售利润为w乙(元)(利润=销售额﹣成本﹣附加费).
(1)、当a=18,且x=100是,w乙=元;(2)、求w甲与x之间的函数关系式(不必写出x的取值范围),当w甲=15000时,若使销售量最大,求x的值;(3)、为完成x件的年销售任务,请你通过分析帮助公司决策,应选择在甲地还是在乙地销售才能使该公司所获年利润最大.23. 已知:如图,在△ABC 中,AB=AC,AE是角平分线,BM平分∠ABC交AE于点 M,经过B,M两点的 ⊙O交BC于点G,交AB于点F,FB恰为⊙O的直径.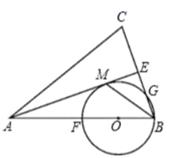 (1)、求证:AE与⊙O相切;(2)、当 BC=4,AC=6,求⊙O 的半径.24. 阅读下面的材料:
(1)、求证:AE与⊙O相切;(2)、当 BC=4,AC=6,求⊙O 的半径.24. 阅读下面的材料:按照一定顺序排列着的一列数称为数列,数列中的每一个数叫做这个数列的项.排在第一位的数称为第一项,记为a1 , 排在第二位的数称为第二项,记为a2 , 依此类推,排在第n位的数称为第n项,记为an , 所以,数列的一般形式可以写成:a1 , a2 , a3 , …,an , ….
一般地,如果一个数列从第二项起,每一项与它前一项的差等于同一个常数,那么这个数列叫做等差数列,这个常数叫做等差数列的公差,公差通常用d表示.
如:数列1,3,5,7,…为等差数列,其中a1=1,a2=3,公差为d=2.
根据以上材料,解答下列问题:
(1)、等差数列5,10,15,…的公差d为 , 第5项是 .(2)、如果一个数列a1 , a2 , a3 , …,an , …,是等差数列,且公差为d,那么根据定义可得到:a2﹣a1=d,a3﹣a2=d,a4﹣a3=d,…,an﹣an﹣1=d,….所以a2=a1+d,a3=a2+d=(a1+d)+d=a1+2d,a4=a3+d=(a1+2d)+d=a1+3d,….由此,请你填空完成等差数列的通项公式:an=a1+()d.(3)、﹣4045是不是等差数列﹣5,﹣7,﹣9…的项?如果是,是第几项?25. 如图,已知抛物线y=ax2+bx+c经过A(4,0),B(﹣2,0),C(0,﹣4)三点.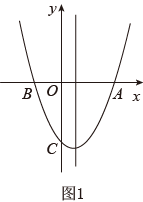
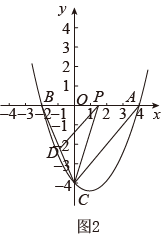 (1)、求抛物线解析式,并求出该抛物线对称轴及顶点坐标;(2)、如图1,点M是抛物线对称轴上的一点,求△MBC周长的最小值;(3)、如图2,P是线段AB上一动点(端点除外),过P作PD AC,交BC于点D,连接CP,求△PCD面积的最大值,并判断当△PCD的面积取最大值的时候,以PA、PD为邻边的平行四边形是否为菱形.26. 如图
(1)、求抛物线解析式,并求出该抛物线对称轴及顶点坐标;(2)、如图1,点M是抛物线对称轴上的一点,求△MBC周长的最小值;(3)、如图2,P是线段AB上一动点(端点除外),过P作PD AC,交BC于点D,连接CP,求△PCD面积的最大值,并判断当△PCD的面积取最大值的时候,以PA、PD为邻边的平行四边形是否为菱形.26. 如图 (1)、如图1,在 ABC中,AB>AC,点D,E分别在边AB、AC上,且DE∥BC,若AD=2,AE= , 则 的值是 .(2)、如图2,在(1)的条件下,将△ADE绕点A逆时针方向旋转一定的角度,连接CE和BD, 的值变化吗?若变化,请说明理由;若不变化,请求出不变的值;(3)、如图3,在Rt△ABC中,∠ACB=90°, , 点M、N分别在边AB,AC上,且MN∥BC,现将△AMN绕点A逆时针方向旋转到△ADE的位置,连接BD和CD,若∠BAC=∠ADC,MN=3,CD=6,请直接写出线段BD的长度.
(1)、如图1,在 ABC中,AB>AC,点D,E分别在边AB、AC上,且DE∥BC,若AD=2,AE= , 则 的值是 .(2)、如图2,在(1)的条件下,将△ADE绕点A逆时针方向旋转一定的角度,连接CE和BD, 的值变化吗?若变化,请说明理由;若不变化,请求出不变的值;(3)、如图3,在Rt△ABC中,∠ACB=90°, , 点M、N分别在边AB,AC上,且MN∥BC,现将△AMN绕点A逆时针方向旋转到△ADE的位置,连接BD和CD,若∠BAC=∠ADC,MN=3,CD=6,请直接写出线段BD的长度.