浙教版备考2022年中考数学二轮复习训练题5:函数应用题
试卷更新日期:2022-03-15 类型:二轮复习
一、单选题
-
1. 已知A , B两地相距60km,甲从A地去B地,乙从B地去A地,图中l1 , l2分别表示甲、乙两人离B地的距离y(km)与甲出发时间x(h)的函数关系图象.设两人相遇在P处,则PA的距离为( )
 A、42km B、28km C、24km D、18km2. 甲、乙两车分别从 、 两地同时出发,沿同一条公路相向而行,相遇时甲、乙所走路程的比为2:3,甲、乙两车离 中点 路程 (千米)与甲车出发时间 (时)的关系图象如图所示,则下列说法错误的是( )
A、42km B、28km C、24km D、18km2. 甲、乙两车分别从 、 两地同时出发,沿同一条公路相向而行,相遇时甲、乙所走路程的比为2:3,甲、乙两车离 中点 路程 (千米)与甲车出发时间 (时)的关系图象如图所示,则下列说法错误的是( ) A、乙车的速度为90千米/时 B、 的值为 C、 的值为150 D、当甲、乙车相距30千米时,甲行走了 或3. 14:00时,时钟中时针与分针的位置如图所示(分针在射线OA上),设经过xmin(0≤x≤30),时针、分针与射线OA所成角的度数分别为y1°、y2°,则y1、y2与x之间的函数关系图是 ( )
A、乙车的速度为90千米/时 B、 的值为 C、 的值为150 D、当甲、乙车相距30千米时,甲行走了 或3. 14:00时,时钟中时针与分针的位置如图所示(分针在射线OA上),设经过xmin(0≤x≤30),时针、分针与射线OA所成角的度数分别为y1°、y2°,则y1、y2与x之间的函数关系图是 ( ) A、
A、 B、
B、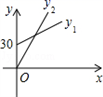 C、
C、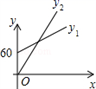 D、
D、 4. 甲,乙两车分别从A, B两地同时出发,相向而行.乙车出发2h后休息,当两车相遇时,两车立即按原速度继续向目的地行驶.设甲车行驶的时间为x(h), 甲,乙两车到B地的距离分别为y1(km), y2(km), y1 , y2关于x的函数图象如图.下列结论:①甲车的速度是 km/h;②乙车休息了0.5h;③两车相距a km时,甲车行驶了 h.正确的是( )
4. 甲,乙两车分别从A, B两地同时出发,相向而行.乙车出发2h后休息,当两车相遇时,两车立即按原速度继续向目的地行驶.设甲车行驶的时间为x(h), 甲,乙两车到B地的距离分别为y1(km), y2(km), y1 , y2关于x的函数图象如图.下列结论:①甲车的速度是 km/h;②乙车休息了0.5h;③两车相距a km时,甲车行驶了 h.正确的是( ) A、①② B、①③ C、②③ D、①②③5. 如图,等边三角形 中, ,动点 从点 出发,以每秒2个单位的速度沿折线 的路径向点 运动,同时动点 也从点 出发,沿线段 以每秒1个单位的速度向点 运动,连接 ,设点 , 的运动时间为 , 的面积为 ,则能反映 与 之间函数关系的图象是( )
A、①② B、①③ C、②③ D、①②③5. 如图,等边三角形 中, ,动点 从点 出发,以每秒2个单位的速度沿折线 的路径向点 运动,同时动点 也从点 出发,沿线段 以每秒1个单位的速度向点 运动,连接 ,设点 , 的运动时间为 , 的面积为 ,则能反映 与 之间函数关系的图象是( )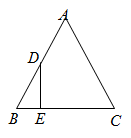 A、
A、 B、
B、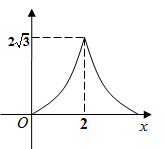 C、
C、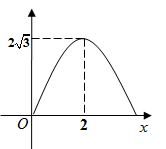 D、
D、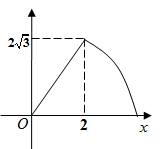 6. 足球运动员将足球沿与地面成一定角度的方向踢出,足球飞行的路线是一条抛物线,不考虑空气阻力,足球距离地面的高度h(单位:m)与足球被踢出后经过的时间t(单位:s)之间的关系如表:
6. 足球运动员将足球沿与地面成一定角度的方向踢出,足球飞行的路线是一条抛物线,不考虑空气阻力,足球距离地面的高度h(单位:m)与足球被踢出后经过的时间t(单位:s)之间的关系如表:t
0
1
2
3
4
5
6
7
…
h
0
8
14
18
20
20
18
14
…
下列结论:①足球距离地面的最大高度超过20m;②足球飞行路线的对称轴是直线t= ;③点(9,0)在该抛物线上;④足球被踢出5s~7s时,距离地面的高度逐渐下降.其中正确的结论是( )
A、②③ B、①②③ C、①②③④ D、②③④7. 学校卫生间的洗手盘台面上有一瓶洗手液(如图①).小丽经过测量发现:洗手液瓶子的截面图下部分是矩形CGHD,洗手液瓶子的底面直径GH=12cm,D,H与喷嘴位置点B三点共线.当小丽按住顶部A下压至如图②位置时,洗手液从喷口B流出(此时喷嘴位置点B距台面的距离为16cm),路线近似呈抛物线状,小丽在距离台面15cm处接洗手液时,手心Q到直线DH的水平距离为4cm,若小丽不去接,则洗手液落在台面的位置距DH的水平距离是16cm.根据小丽测量所得数据,可得洗手液喷出时的抛物线函数解析式的二次项系数是( )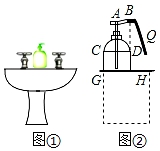 A、﹣ B、 C、﹣ D、8. 如图,矩形ABCD各边中点分别是E、F、G、H,AB=2 ,BC=2,M为AB上一动点,过点M作直线l⊥AB,若点M从点A开始沿着AB方向移动到点B即停(直线l随点M移动),直线l扫过矩形内部和四边形EFGH外部的面积之和记为S.设AM=x,则S关于x的函数图象大致是( )
A、﹣ B、 C、﹣ D、8. 如图,矩形ABCD各边中点分别是E、F、G、H,AB=2 ,BC=2,M为AB上一动点,过点M作直线l⊥AB,若点M从点A开始沿着AB方向移动到点B即停(直线l随点M移动),直线l扫过矩形内部和四边形EFGH外部的面积之和记为S.设AM=x,则S关于x的函数图象大致是( ) A、
A、 B、
B、 C、
C、 D、
D、 9. 甲、乙两人在笔直的公路上同起点、同终点、同方向匀速步行1200米,先到终点的人原地休息、已知甲先出发3分钟,在整个步行过程中,甲、乙两人之间的距离y(米)与甲出发的时间t (分)之间的关系如图所示,下列结论:①乙用6分钟追上甲;②乙步行的速度为60米/分;③乙到达终点时,甲离终点还有400米;④整个过程中,甲乙两人相聚180米有2个时刻,分别是t=18和t=24.其中正确的结论有( )
9. 甲、乙两人在笔直的公路上同起点、同终点、同方向匀速步行1200米,先到终点的人原地休息、已知甲先出发3分钟,在整个步行过程中,甲、乙两人之间的距离y(米)与甲出发的时间t (分)之间的关系如图所示,下列结论:①乙用6分钟追上甲;②乙步行的速度为60米/分;③乙到达终点时,甲离终点还有400米;④整个过程中,甲乙两人相聚180米有2个时刻,分别是t=18和t=24.其中正确的结论有( ) A、①② B、①③ C、②④ D、①②④10. 如图,线段 ,点 、 在 上, .已知点 从点 出发,以每秒1个单位长度的速度沿着 向点 移动,到达点 后停止移动,在点 移动过程中作如下操作:先以点 为圆心, 、 的长为半径分别作两个圆心角均为60°的扇形,再将两个扇形分别围成两个圆锥的侧面.设点 的移动时间为(秒).两个圆锥的底面面积之和为 .则 关于 的函数图象大致是( )
A、①② B、①③ C、②④ D、①②④10. 如图,线段 ,点 、 在 上, .已知点 从点 出发,以每秒1个单位长度的速度沿着 向点 移动,到达点 后停止移动,在点 移动过程中作如下操作:先以点 为圆心, 、 的长为半径分别作两个圆心角均为60°的扇形,再将两个扇形分别围成两个圆锥的侧面.设点 的移动时间为(秒).两个圆锥的底面面积之和为 .则 关于 的函数图象大致是( )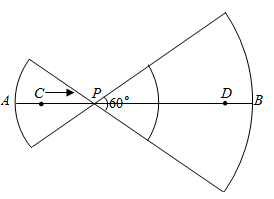 A、
A、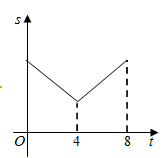 B、
B、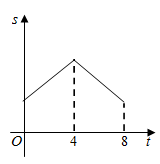 C、
C、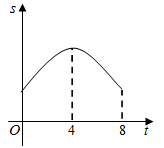 D、
D、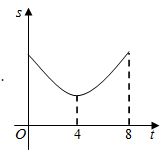
二、填空题
-
11. 如图,有一矩形养鸡场,养鸡场的一边靠墙(墙足够长),另三边用米的长篱笆围成,则矩形面积的最大值是平方米.
 12. 某商户购进某种商品的进价是50元/个,根据市场调研发现售价是80元/个时,每月可卖出200个,若销售单价每降低1元,则每月可多卖出10个,同样若销售单价每增加1元,则每月可少卖出10个.若计划下月该商品的销售利润不低于5760元,则该商品的销售单价x(元)的取值范围是 .13. 如图所示,从高为2m的点 处向右上抛一个小球 ,小球路线呈抛物线 形状,小球水平经过2m时达到最大高度6m,然后落在下方台阶B处弹起,已知 m, m, m,若小球弹起形成一条与 形状相同的抛物线,且落点 与 , 在同一直线上,则小球弹起时的最大高度是m
12. 某商户购进某种商品的进价是50元/个,根据市场调研发现售价是80元/个时,每月可卖出200个,若销售单价每降低1元,则每月可多卖出10个,同样若销售单价每增加1元,则每月可少卖出10个.若计划下月该商品的销售利润不低于5760元,则该商品的销售单价x(元)的取值范围是 .13. 如图所示,从高为2m的点 处向右上抛一个小球 ,小球路线呈抛物线 形状,小球水平经过2m时达到最大高度6m,然后落在下方台阶B处弹起,已知 m, m, m,若小球弹起形成一条与 形状相同的抛物线,且落点 与 , 在同一直线上,则小球弹起时的最大高度是m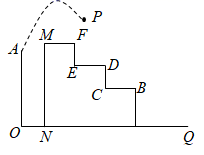 14. 如图1是某校园运动场主席台及遮阳棚,其侧面结构示意图如图2所示.主席台(矩形ABCD)高AD=2米,直杆DE=6米,斜拉杆EG,EH起稳固作用,点H处装有一射灯.遮阳棚边缘曲线FHG可近似看成抛物线的一部分,G为抛物线的最高点且位于主席台边缘BC的正上方,若点E,H,C在同一直线上,且DF=1米,EG=6米,∠AEG=60°,则射灯H离地面的高度为 米.
14. 如图1是某校园运动场主席台及遮阳棚,其侧面结构示意图如图2所示.主席台(矩形ABCD)高AD=2米,直杆DE=6米,斜拉杆EG,EH起稳固作用,点H处装有一射灯.遮阳棚边缘曲线FHG可近似看成抛物线的一部分,G为抛物线的最高点且位于主席台边缘BC的正上方,若点E,H,C在同一直线上,且DF=1米,EG=6米,∠AEG=60°,则射灯H离地面的高度为 米. 15. 如图1,在矩形 中,动点P从点A出发,沿 的方向在AB和BC上运动,记 ,点D到直线PA的距离为y , 且y关于x的函数图象如图2所示.当 的面积与 的面积相等时,y的值为 .
15. 如图1,在矩形 中,动点P从点A出发,沿 的方向在AB和BC上运动,记 ,点D到直线PA的距离为y , 且y关于x的函数图象如图2所示.当 的面积与 的面积相等时,y的值为 .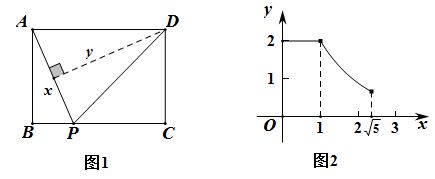 16. 如图1是甲、乙两个圆柱形容器的轴截面示意图,乙容器中有一个圆柱形铁块立放其中(圆柱形铁块的下底面完全落在乙容器底面上),现将甲容器中的水匀速注入乙容器,甲、乙两个容器中水的深度与注水时间(分钟)之间的关系如图2所示,若乙容器中铁块的体积是 , 则甲容器的底面积是 .
16. 如图1是甲、乙两个圆柱形容器的轴截面示意图,乙容器中有一个圆柱形铁块立放其中(圆柱形铁块的下底面完全落在乙容器底面上),现将甲容器中的水匀速注入乙容器,甲、乙两个容器中水的深度与注水时间(分钟)之间的关系如图2所示,若乙容器中铁块的体积是 , 则甲容器的底面积是 .
三、综合题
-
17. 为响应国家“篮球进校园”的号召,某校购买了50个A型篮球和20个B型篮球共花费5000元,已知购买一个B型篮球比购买一个A型篮球多花40元.(1)、求购买一个A型篮球和一个B型篮球各需多少元;(2)、通过全校师生的共同努力,今年该校被评为“篮球特色学校”,学校计划用不超过4600元的经费再次购买A型篮球和B型篮球共50个,其中B型篮球的数量不少于A型篮球数量的 , 求A型篮球数量的取值范围;(3)、报价如下表:
型号
购买数量少于30个
购买数量不少于30个
A型
原价购买
打九折
B型
原价购买
打八折
在(2)的条件下,设购买总花费为w元,问如何购买使得总花费w最少?请说明理由.
18. 上午8点,某台风中心在A岛正南方向 处由南向北匀速移动,同时在A岛正西方向 处有一艘补给船向A岛匀速驶来,补给完后改变速度立即向A岛正北方向的C港匀速驶去,如图所示是台风中心、补给船与A岛的距离S和时间t的图象.已知台风影响的半径是 (包含边界),请结合图象解答下列问题: (1)、台风的速度是 ,补给船在到达A岛前的速度是 ,图中点P的实际意义是;(2)、从几点开始,补给船将受到台风的影响?(3)、设补给船驶出A岛到驶到C港之前受到台风影响的时间为a小时,出于安全考虑,补给船速度不超过 、 .求出图中补给船航行时间m的正整数值及此时补给船在驶入C港之前受台风影响的总时间.19. 某土产公司组织20辆汽车装运甲、乙、丙三种土特产共120吨去外地销售.按计划20辆车都要装运,每辆汽车只能装运同一种土特产,且必须装满.根据下表提供的信息,解答以下问题:
(1)、台风的速度是 ,补给船在到达A岛前的速度是 ,图中点P的实际意义是;(2)、从几点开始,补给船将受到台风的影响?(3)、设补给船驶出A岛到驶到C港之前受到台风影响的时间为a小时,出于安全考虑,补给船速度不超过 、 .求出图中补给船航行时间m的正整数值及此时补给船在驶入C港之前受台风影响的总时间.19. 某土产公司组织20辆汽车装运甲、乙、丙三种土特产共120吨去外地销售.按计划20辆车都要装运,每辆汽车只能装运同一种土特产,且必须装满.根据下表提供的信息,解答以下问题:土特产种类
甲
乙
丙
每辆汽车运载量(吨)
8
6
5
每吨土特产获利(百元)
12
16
10
(1)、设装运甲种土特产的车辆数为 ,装运乙种土特产的车辆数为 ,求 与 之间的函数关系式.(2)、如果装运每辆土特产的车辆都不少于3辆,那么车辆的安排方案有几种?并写出每种安排方案.(3)、若要使此次销售获利最大,应采用(2)中哪种安排方案?并求出最大利润的值.20. 甲、乙两名实验者在A、B两个实验室进行空调制冷后舒适度测试,两人同时启动空调1小时后,开始记录数据,经过数据分析,甲的舒适指数与空调启动时间成反比例关系,乙的舒适指数与空调启动时间的函数关系式为 , 函数图象如图所示且在2小时,乙的舒适指数最大. (1)、求m、k;(2)、当时,求的较大值;(3)、若规定舒适度小于1时,实验室则不适合人长时间逗留,求至少启动空调多少小时后,两个实验室均不适合人长时间逗留.21. 某企业决定从甲、乙两种产品中选择一种生产,打入国际市场,已知生产销售这两种产品的有关数据如表:(单位:万元)
(1)、求m、k;(2)、当时,求的较大值;(3)、若规定舒适度小于1时,实验室则不适合人长时间逗留,求至少启动空调多少小时后,两个实验室均不适合人长时间逗留.21. 某企业决定从甲、乙两种产品中选择一种生产,打入国际市场,已知生产销售这两种产品的有关数据如表:(单位:万元)年固定成本
每件产品成本
每件产品销售价
甲产品
20
a
10
乙产品
40
8
18
a为常数,且3≤a≤8.甲产品每年最多可生产销售200件,乙产品每年最多可生产销售80件,销售乙产品x件时需另外上交0.05x2万元的特别关税.
(1)、写出该企业生产销售乙产品的年利润y关于x的函数表达式为.(2)、当销售乙产品多少件时,可获乙产品的利润最大?最大利润是多少?(3)、该企业选择哪一种产品生产销售可获得最大年利润?请说明理由.22. 合肥市某水产养殖户进行小龙虾养殖.已知每千克小龙虾养殖成本为6元,在整个销售旺季的80天里,销售单价 (元/千克)与时间第 (天)之间的函数关系为:,日销售量 (千克)与时间第 (天)之间的函数关系如图所示:
 (1)、哪一天的日销售利润最大?最大利润是多少?(2)、该养殖户有多少天日销售利润不低于2400元?(3)、在实际销售的前40天中,该养殖户决定每销售1千克小龙虾,就捐赠 元给村里的特困户.在这前40天中,每天扣除捐赠后的日销售利润随时间 的增大而增大,求 的取值范围.23. 某公司生产A型活动板房成本是每个425元。图①表示A型活动板房的一面墙,它由长方形和抛物线构成,长方形的长AD=4m,宽AB=3m,抛物线的最高点E到BC的距离为4m。
(1)、哪一天的日销售利润最大?最大利润是多少?(2)、该养殖户有多少天日销售利润不低于2400元?(3)、在实际销售的前40天中,该养殖户决定每销售1千克小龙虾,就捐赠 元给村里的特困户.在这前40天中,每天扣除捐赠后的日销售利润随时间 的增大而增大,求 的取值范围.23. 某公司生产A型活动板房成本是每个425元。图①表示A型活动板房的一面墙,它由长方形和抛物线构成,长方形的长AD=4m,宽AB=3m,抛物线的最高点E到BC的距离为4m。 (1)、按如图①所示的直角坐标系,抛物线可以用y=kx2+m(k+0)表示,求该抛物线的函数表达式;(2)、现将A型活动板房改造为B型活动板房。如图②,在抛物线与AD之间的区域内加装一扇长方形窗户FGMN,点G,M在AD上,点N,F在抛物线上,窗户的成本为50元/m2。已知GM= 2m,求每个B型活动板房的成本是多少?(每个B型活动板房的成本=每个A
(1)、按如图①所示的直角坐标系,抛物线可以用y=kx2+m(k+0)表示,求该抛物线的函数表达式;(2)、现将A型活动板房改造为B型活动板房。如图②,在抛物线与AD之间的区域内加装一扇长方形窗户FGMN,点G,M在AD上,点N,F在抛物线上,窗户的成本为50元/m2。已知GM= 2m,求每个B型活动板房的成本是多少?(每个B型活动板房的成本=每个A型活动板房的成本+扇窗户FGMN的成本)
(3)、根据市场调查,以单价650元销售(2)中的B型活动板房,每月能售出100个,而单价每降低10元,每月能多售出20个。公司每月最多能生产160个B型活动板房。不考虑其他因素,公司将销售单价n(元)定为多少时,每月销售B型活动板房所获利润w(元)最大?最大利润是多少?24. 女生排球考试要求:垫球后,球在运动中离地面的最大高度至少为2米.某次模拟测试中,某女生在O处将球垫偏,之后又在A, B两处先后垫球,球沿抛物线C1 → C2 → C3运动(假设抛物线C1 , C2 , C3在同一平面内),最终正好在O处垫住,O处离地面的距离为1米.如图所示,以O为坐标原点1米为单位长度建立直角坐标系,x轴平行于地面水平直线m,已知点A( , ),点B的横坐标为 - ,抛物线C1和C3的表达式分别为 y = ax2- 2ax 和 y = 2ax2 + bx (a≠ 0).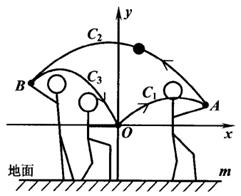 (1)、求抛物线C1的函数表达式.(2)、第一次垫球后,球在运动中离地面的最大高度是否达到要求?请说明理由.(3)、为了使第三次垫球后,球在运动中离地面的最大高度达到要求,该女生第三次垫球处B 离地面的高度至少为多少米?
(1)、求抛物线C1的函数表达式.(2)、第一次垫球后,球在运动中离地面的最大高度是否达到要求?请说明理由.(3)、为了使第三次垫球后,球在运动中离地面的最大高度达到要求,该女生第三次垫球处B 离地面的高度至少为多少米?