浙教版备考2022年中考数学二轮复习训练题3:反比例函数
试卷更新日期:2022-03-15 类型:二轮复习
一、单选题
-
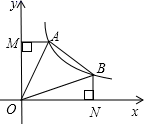
1. 若正比例函数y=2kx与反比例函数(k≠0)的图象交于点A(m,1),则k的值是( )A、或 B、或 C、 D、2. 如图,若一次函数与反比例函数的图象交两点,过点B作轴,垂足为C,且 , 则不等式的解集为( )
 A、或 B、或 C、或 D、或3. 如图,直线 与 轴、 轴分别相交于点A、B,过点B作 ,使 .将 绕点 顺时针旋转,每次旋转 .则第2022次旋转结束时,点 的对应点 落在反比例函数 的图象上,则 的值为
A、或 B、或 C、或 D、或3. 如图,直线 与 轴、 轴分别相交于点A、B,过点B作 ,使 .将 绕点 顺时针旋转,每次旋转 .则第2022次旋转结束时,点 的对应点 落在反比例函数 的图象上,则 的值为 A、-4 B、4 C、-6 D、64. 如图,在平面直角坐标系中,平行四边形的边交轴于点 , 反比例函数( , )的图象经过上的两点 , .若 , , 平行四边形的面积为7,则的值为( )
A、-4 B、4 C、-6 D、64. 如图,在平面直角坐标系中,平行四边形的边交轴于点 , 反比例函数( , )的图象经过上的两点 , .若 , , 平行四边形的面积为7,则的值为( ) A、 B、 C、2 D、5. 如图,在平面直角坐标系中,菱形ABCO的顶点O在坐标原点,且与反比例函数y=的图象相交于A(m,3),C两点,已知点B( , ),则k的值为( )
A、 B、 C、2 D、5. 如图,在平面直角坐标系中,菱形ABCO的顶点O在坐标原点,且与反比例函数y=的图象相交于A(m,3),C两点,已知点B( , ),则k的值为( ) A、-6 B、-6 C、-12 D、-126. 如图,点A是函数y= 的图象上的点,点B,C的坐标分别为B(﹣ ,﹣ ),C( , ).试利用性质:“函数y= 的图象上任意一点A都满足|AB﹣AC|=2 ”求解下面问题:作∠BAC的角平分线AE,过B作AE的垂线交AE于F,已知当点A在函数y= 的图象上运动时,点F总在一条曲线上运动,则这条曲线为( )
A、-6 B、-6 C、-12 D、-126. 如图,点A是函数y= 的图象上的点,点B,C的坐标分别为B(﹣ ,﹣ ),C( , ).试利用性质:“函数y= 的图象上任意一点A都满足|AB﹣AC|=2 ”求解下面问题:作∠BAC的角平分线AE,过B作AE的垂线交AE于F,已知当点A在函数y= 的图象上运动时,点F总在一条曲线上运动,则这条曲线为( )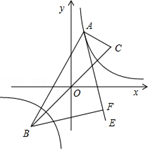 A、直线 B、抛物线 C、圆 D、反比例函数的曲线7. 如图,在直角坐标系 中,已知点A,点 分别是 轴和 轴上的点,过 轴上的另一点 作 ,与反比例函数 的图象交于 、 两点, 恰好为 的中点,连结 和 .若 , 的面积为 ,则 的值为( )
A、直线 B、抛物线 C、圆 D、反比例函数的曲线7. 如图,在直角坐标系 中,已知点A,点 分别是 轴和 轴上的点,过 轴上的另一点 作 ,与反比例函数 的图象交于 、 两点, 恰好为 的中点,连结 和 .若 , 的面积为 ,则 的值为( ) A、3 B、 C、2 D、18. 如图,在平面直角坐标系xOy中,菱形ABCD与菱形GFED关于点D成中心对称,点C,G在x轴的正半轴上,点A,F在反比例函数y= (k>0,x>0)的图象上,延长AB交x轴于点P(1,0),若∠APO=120°,则k的值是( )
A、3 B、 C、2 D、18. 如图,在平面直角坐标系xOy中,菱形ABCD与菱形GFED关于点D成中心对称,点C,G在x轴的正半轴上,点A,F在反比例函数y= (k>0,x>0)的图象上,延长AB交x轴于点P(1,0),若∠APO=120°,则k的值是( )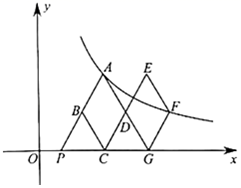 A、3 B、3 C、6 D、69. 我们知道,方程x²+2x-1=0的解可看作函数y=x+2的图象与函数y= 的图象交点的横坐标。那么方程kx²+x-4=0(k≠0)的两个解其实就是直线y=kx+1与双曲线y= 的图象交点的横坐标。若这两个交点所对应的坐标为(x1 , )、(x2 , ),且均在直线y=x的同侧,则实数k的取值范围是( )A、 <k< B、 <k< C、 <k<0或0<k< D、 <k< 或 <k<010. 如图,点P是函数y= (k1>0,x>0)的图象上一点,过点P分别作x轴和y轴的垂线,垂足分别为点A、B,交函数y= (k2>0,x>0)的图象于点C、D,连接OC、OD、CD、AB,其中k1>k2.下列结论:①CD∥AB;②S△OCD= ;③S△DCP= ,其中正确的是( )
A、3 B、3 C、6 D、69. 我们知道,方程x²+2x-1=0的解可看作函数y=x+2的图象与函数y= 的图象交点的横坐标。那么方程kx²+x-4=0(k≠0)的两个解其实就是直线y=kx+1与双曲线y= 的图象交点的横坐标。若这两个交点所对应的坐标为(x1 , )、(x2 , ),且均在直线y=x的同侧,则实数k的取值范围是( )A、 <k< B、 <k< C、 <k<0或0<k< D、 <k< 或 <k<010. 如图,点P是函数y= (k1>0,x>0)的图象上一点,过点P分别作x轴和y轴的垂线,垂足分别为点A、B,交函数y= (k2>0,x>0)的图象于点C、D,连接OC、OD、CD、AB,其中k1>k2.下列结论:①CD∥AB;②S△OCD= ;③S△DCP= ,其中正确的是( ) A、①②③ B、①② C、②③ D、①③
A、①②③ B、①② C、②③ D、①③二、填空题
-
11. 如图,矩形 的顶点A在y轴的正半轴上,顶点C在x轴的正半轴上,反比例函数 在第一象限内的图象分别与边 、 相交于点D、E.连结 , ,恰有 , ,若 ,则k的值是.
 12. 如图,在平面直角坐标系中,菱形ABCD的顶点A与原点O重合,点C在直线y=x_上,点B的坐标为(2,1)将菱形ABCD沿直线y=x平移,当点B,D同时落在反比例函数y= (x>0)的图象上时,菱形沿直线y=x平移的距离为。
12. 如图,在平面直角坐标系中,菱形ABCD的顶点A与原点O重合,点C在直线y=x_上,点B的坐标为(2,1)将菱形ABCD沿直线y=x平移,当点B,D同时落在反比例函数y= (x>0)的图象上时,菱形沿直线y=x平移的距离为。 13. 如图,在x轴正半轴上依次截取OA1=A1A2=A2A…An﹣1An(n为正整数),过点A1、A2、A3、…、An分别作x轴的垂线,与反比例函数y= (x>0)交于点P1、P2、P3、…、Pn , 连接P1P2、P2P3、…、Pn﹣1Pn , 过点P2、P3、…、Pn分别向P1A1、P2A2、…、Pn﹣1An﹣1作垂线段,构成的一系列直角三角形(见图中阴影部分)的面积和是
13. 如图,在x轴正半轴上依次截取OA1=A1A2=A2A…An﹣1An(n为正整数),过点A1、A2、A3、…、An分别作x轴的垂线,与反比例函数y= (x>0)交于点P1、P2、P3、…、Pn , 连接P1P2、P2P3、…、Pn﹣1Pn , 过点P2、P3、…、Pn分别向P1A1、P2A2、…、Pn﹣1An﹣1作垂线段,构成的一系列直角三角形(见图中阴影部分)的面积和是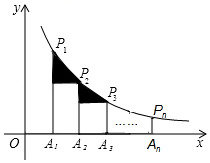 14. 如图,一次函数 与反比例函数 的图象交于点A,B,点P在以 为圆心,1为半径的⊙C上,Q是 的中点,若 长的最大值为 ,则k的值为.
14. 如图,一次函数 与反比例函数 的图象交于点A,B,点P在以 为圆心,1为半径的⊙C上,Q是 的中点,若 长的最大值为 ,则k的值为.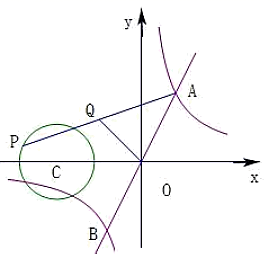 15. 如图,在平面直角坐标系 中,点 坐标为 ,以 为对角线作正方形 ,若顶点 在反比例函数 的图象上, 的值是.
15. 如图,在平面直角坐标系 中,点 坐标为 ,以 为对角线作正方形 ,若顶点 在反比例函数 的图象上, 的值是. 16. 如图,直线 与双曲线 交于 、 两点,连接 、 , 轴于 , 轴于 ,设 , 的解析式分别为 , ,现有以下结论:
16. 如图,直线 与双曲线 交于 、 两点,连接 、 , 轴于 , 轴于 ,设 , 的解析式分别为 , ,现有以下结论:① ;② ;③若 ,则 ;④ 有最小值.
其中正确的是.(写出所有正确结论的序号)
三、综合题
-
17. 已知反比例函数 图象经过一、三象限.(1)、判断点 在第几象限(2)、若点 , 是反比例函数 图象上的两点,试比较a,b,c的大小关系(3)、设反比例函数 ,已知 ,且满足当 时,函数 的最大值是 ;当 时,函数 的最小值是 .求x为何值时, .18. 已知反比例函数 ( 为常数)的图象在一、三象限.
 (1)、求m的取值范围.(2)、如图,若该反比例函数的图象经过 ABCD的顶点D,点A,B的坐标分别为(0,3),(-2,0).
(1)、求m的取值范围.(2)、如图,若该反比例函数的图象经过 ABCD的顶点D,点A,B的坐标分别为(0,3),(-2,0).①求出反比例函数表达式;
②设点P是该反比例函数图象上的一点,若OD=OP,则P点的坐标为▲ .若以D,O,P为顶点的三角形是等腰三角形,则满足条件的点P的个数为▲ .
19. 综合与探究如图,矩形的顶点O与坐标原点重合,边 , 分别落在轴和轴上,顶点B的坐标(8,4),点D是边上一动点,过点D作反比例函数的图象与矩形的边交于点E.
 (1)、如图1,连接 , , 若 .
(1)、如图1,连接 , , 若 .①填空:点D的坐标为 ▲ , 点E的坐标为 ▲ ;
②请判断线段与的位置关系,并说明理由.
(2)、如图2,连接 , , 若线段平分 .①求k的值;
②若动点M在y轴上运动,当线段与的差最大时,请直接写出点M的坐标.
20. 如图,在平面直角坐标系中,矩形OABC的顶点B的坐标为(4,2),OA,OC分别在x轴和y轴正半轴上,连接OB.将△OAB绕点O逆时针旋转,得到△ODE,点A的对应点为点D,点B的对应点为点E,且点E在y轴正半轴上,OD与CB相交于点F,反比例函数y (x>0)的图象经过点F,交AB于点G. (1)、点F的坐标为;k=;(2)、连接FG,求证:△OCF∽△FBG;(3)、点M在直线OD上,点N是平面内一点,当四边形GFMN是正方形时,请直接写出点N的坐标.21. 如图,矩形ABCD的两边AD、AB的长分别为3、8,边BC落在x轴上,E是DC的中点,连接AE.
(1)、点F的坐标为;k=;(2)、连接FG,求证:△OCF∽△FBG;(3)、点M在直线OD上,点N是平面内一点,当四边形GFMN是正方形时,请直接写出点N的坐标.21. 如图,矩形ABCD的两边AD、AB的长分别为3、8,边BC落在x轴上,E是DC的中点,连接AE.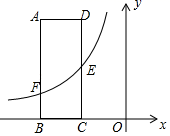 (1)、若点B坐标为(﹣6,0),求直线AE的表达式;(2)、反比例函数y=(x<0)的图象经过点E,与AB交于点F,若AF﹣AE=2,求反比例函数的表达式;(3)、在(2)的条件下,连接矩形ABCD两对边AD与BC的中点M、N,设线段MN与反比例函数图象交于点P,将线段MN沿x轴向右平移n个单位,若MP<NP,直接写出n的取值范围.22. 如图,在平面直角坐标系中,直线y=-x+5与反比例函数y= (x>0)的图象相交于点A(3,a)和点B(b , 3),点D , C分别是x轴和y轴的正半轴上的动点,且满足
(1)、若点B坐标为(﹣6,0),求直线AE的表达式;(2)、反比例函数y=(x<0)的图象经过点E,与AB交于点F,若AF﹣AE=2,求反比例函数的表达式;(3)、在(2)的条件下,连接矩形ABCD两对边AD与BC的中点M、N,设线段MN与反比例函数图象交于点P,将线段MN沿x轴向右平移n个单位,若MP<NP,直接写出n的取值范围.22. 如图,在平面直角坐标系中,直线y=-x+5与反比例函数y= (x>0)的图象相交于点A(3,a)和点B(b , 3),点D , C分别是x轴和y轴的正半轴上的动点,且满足CD∥AB.
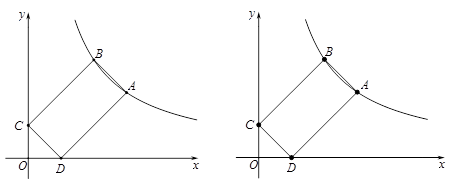 (1)、求a , b的值及反比例函数的解析式;(2)、若OD=1,求点C的坐标,判断四边形ABCD的形状并说明理由;(3)、若点M是反比例函数y= (x>0)图象上的一个动点,当△AMD是以AM为直角边的等腰直角三角形时,求点M的坐标.23. 九年级某数学兴趣小组在学习了反比例函数的图象与性质后,进一步研究函数 的图象与性质.其探究过程如下:(1)、绘制函数图象,如图.
(1)、求a , b的值及反比例函数的解析式;(2)、若OD=1,求点C的坐标,判断四边形ABCD的形状并说明理由;(3)、若点M是反比例函数y= (x>0)图象上的一个动点,当△AMD是以AM为直角边的等腰直角三角形时,求点M的坐标.23. 九年级某数学兴趣小组在学习了反比例函数的图象与性质后,进一步研究函数 的图象与性质.其探究过程如下:(1)、绘制函数图象,如图.列表:下表是 与 的几组对应值,其中 ▲ ;
…
-3
-2
-1
1
2
3
…
…
1
3
9
9
3
1
…
描点:根据表中各组对应值 ,在平面直角坐标系中描出了各点:
连线:用平滑的曲线顺次连接各点,画出了部分图象,请你把图象补充完整;
 (2)、通过观察图象,写出该函数的两条性质:①;②;(3)、①观察发现:若直线 交函数 的图象于 , 两点,连接 ,过点 作 交 轴于 ,则 ;
(2)、通过观察图象,写出该函数的两条性质:①;②;(3)、①观察发现:若直线 交函数 的图象于 , 两点,连接 ,过点 作 交 轴于 ,则 ;②探究思考:将①中“直线 ”改为“直线 ”,其他条件不变,则 ;
③类比猜想:若直线 交函数 的图象于 , 两点,连接 ,过点 作 交轴于 ,则 ;
24. 定义:只有三边相等的四边形称为准菱形.
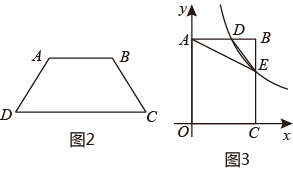 (1)、如图1,图形 (填序号)是准菱形;(2)、如图2,四边形ABCD中,AB∥DC,∠B+∠D=180°,AB=AD,求证:四边形ABCD是准菱形;(3)、如图3,在平面直角坐标系xOy中,矩形OABC的边OA,OC分别落在y轴,x轴上,反比例函数y= (k>0)的图象分别与边AB,BC交于点D,E.已知AD=DE,△ADE的面积为10,AD:DB=5:3,若点F是坐标平面上一点,四边形ADEF是准菱形,当准菱形ADEF面积最大时,求点F的坐标.
(1)、如图1,图形 (填序号)是准菱形;(2)、如图2,四边形ABCD中,AB∥DC,∠B+∠D=180°,AB=AD,求证:四边形ABCD是准菱形;(3)、如图3,在平面直角坐标系xOy中,矩形OABC的边OA,OC分别落在y轴,x轴上,反比例函数y= (k>0)的图象分别与边AB,BC交于点D,E.已知AD=DE,△ADE的面积为10,AD:DB=5:3,若点F是坐标平面上一点,四边形ADEF是准菱形,当准菱形ADEF面积最大时,求点F的坐标.