北师大版备考2022中考数学二轮复习专题3 分式

试卷更新日期：2022-03-14 类型：二轮复习

进入出卷网下载

一、单选题

1. 在代数式 $\frac{3}{a}$ ， $\frac{2 x - 3 y}{4}$ ， $\frac{1}{2} (m - n)$ ， $\frac{x - y}{x + y}$ ， $\frac{1}{π}$ 中属于分式的有（）

A、2个 B、3个 C、4个 D、5个

查看试题解析
2. 下列式子从左到右变形不正确的是（）

A、 $\frac{3 a}{3 b} = \frac{a}{b}$ B、 $\frac{- a}{b} = - \frac{a}{b}$ C、 $\frac{a^{2} + b^{2}}{a + b} = a + b$ D、 $\frac{a - 1}{1 - a} = - 1$

查看试题解析
3. 下列分式中，是最简分式的是（）

A、 $\frac{2 (x + 1)}{x + 1}$ B、 $\frac{a - b}{a + b}$ C、 $\frac{2 a x}{3 a y}$ D、 $\frac{a^{2} - b^{2}}{a - b}$

查看试题解析
4. 若式子 $\frac{\sqrt{x - 2}}{x - 3}$ 有意义，则x的取值范围为（）

A、x≥2 B、x≠3 C、x≤2或x≠3 D、x≥2且x≠3

查看试题解析
5. 计算： ${(- m^{2} n^{3})}^{- 2} =$ （）

A、－ $\frac{1}{m^{4} n^{5}}$ B、－ $m^{4} n^{5}$ C、 $\frac{1}{m^{4} n^{6}}$ D、－ $m^{4} n^{6}$

查看试题解析
6. 若代数式 $\frac{x^{2}}{x - 1} ◯ \frac{x}{x - 1} (x \neq 0)$ 运算结果为x，则在“○”处的运算符号应该是（）

A、除号“÷” B、除号“÷”或减号“-” C、减号“-” D、乘号“×”或减号“-”

查看试题解析
7. 下图的计算过程中，从哪一步开始出现错误（）

A、① B、② C、③ D、④

查看试题解析
8. 已知a＋ $\frac{1}{a}$ ＝ $\sqrt{10}$ ，则a－ $\frac{1}{a}$ 的值为（）

A、±2 $\sqrt{2}$ B、8 C、 $\sqrt{6}$ D、± $\sqrt{6}$

查看试题解析
9. 若 $x$ 是整数，则使分式 $\frac{8 x + 2}{2 x - 1}$ 的值为整数的 $x$ 值有（）个.

A、2 B、3 C、4 D、5

查看试题解析
10. 已知三个数 $a ， b ， c$ 满足 $\frac{a b}{a + b} = \frac{1}{5}$ ， $\frac{b c}{b + c} = \frac{1}{6}$ ， $\frac{c a}{c + a} = \frac{1}{7}$ ，则 $\frac{a b c}{a b + b c + c a}$ 的值是（）

A、 $\frac{1}{9}$ B、 $\frac{1}{6}$ C、 $\frac{2}{15}$ D、 $\frac{1}{20}$

查看试题解析

二、填空题

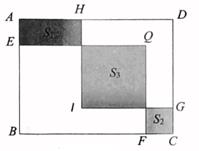
11. 若分式 $\frac{2}{x + 1}$ 无意义，则x的值为.

查看试题解析
12. 当 $x$ 时，分式 $\frac{x - 2}{2 x + 1}$ 的值为零.

查看试题解析
13. 计算：-2²⁺（ $\frac{1}{3}$ ）^-2+（ $π$ - $\sqrt{5}$ ）⁰+ $\sqrt[3]{- 125}$ =.

查看试题解析
14. 如果 $n = 4 m \neq 0$ ，那么代数式 $\frac{3 m - n}{4 m^{2} - n^{2}} \cdot (2 m + n)$ 的值是.

查看试题解析
15. 红细胞也称红血球，是血液中数量最多的一种血细胞，也是我们体内通过血液运送氧气的最主要的媒介，同时还具有免疫功能．红细胞的直径单位一般用微米（μm），1μm＝0.000001m，人类的红细胞直径通常是6μm～8μm.6μm用科学记数法可以表示为m．

查看试题解析
16. 若 $x^{2} - 3 x + 1 = 0$ ，则 $\frac{x^{2}}{x^{4} + x^{2} + 1}$ 的值为

查看试题解析
17. 如图，在长方形ABCD中，AB=10，BC=13．E，F，G，H分别是线段AB，BC，CD，AD上的定点．现分别以BE，BF为边作长方形BEQF，以DG为边作正方形DGIH．若长方形BEQF与正方形DGIH的重合部分恰好是一个正方形，且BE=DG，Q，I均在长方形ABCD内部．记图中的阴影部分面积分别为S₁ ， S₂ ， S₃ ．若 $\frac{S_{2}}{S_{1}} = \frac{3}{7}$ ，则S₃= ．

查看试题解析
18. 已知 ${(x - 2)}^{x^{2} - 4}$ = 1，则 x =（）

查看试题解析

三、计算题

19. 计算： ${(π - 1)}^{0} + \sqrt{8} -$ 4sin45°

查看试题解析
20. 计算 $\frac{1}{x (x + 1)} + \frac{1}{(x + 1) (x + 2)} + \frac{1}{(x + 2) (x + 3)} + \dots + \frac{1}{(x + 2017) (x + 2018)}$ 并求当x=1时，该代数式的值.

查看试题解析
21. 先化简，再求值： $\frac{x^{2}}{x^{2} - 1} \div (\frac{1}{x - 1} + 1)$ ，其中 $x$ 为整数且满足不等式组 ${\begin{array}{l} x - 1 > 1 ， \\ 5 - 2 x \geq - 2. \end{array}$

查看试题解析

四、作图题

22. 平面直角坐标系中，△ABC的位置如图所示（每个小方格都是边长为1个单位长度的正方形）．其中A（1，1）、B（4，4）、C（5，1）．

(1)、将△ABC沿x轴方向向左平移6个单位，画出平移后得到的△A₁B₁C₁ ．

(2)、将△ABC绕着点A顺时针旋转90°，画出旋转后得到的△A₂B₂C₂ ， A、B、C的对应点分别为A₂、B₂、C₂ ．

(3)、先化简，再求值： $(\frac{1}{a - 2} - \frac{2}{a^{2} - 4}) \div \frac{a^{2} - 2 a}{a^{2} - 4}$ ，其中a＝5．

查看试题解析

五、解答题

23. 化简求值： $(1 + \frac{2}{x - 2}) \div \frac{1}{x^{2} - 4} - (2 x + 1)$ ，其中 $x = \sqrt{7}$ .

查看试题解析
24. 阅读材料：
（ 1 ）1的任何次幂都为1；

（ 2 ）-1的奇数次幂为-1；

（ 3 ）-1的偶数次幂为1；

（ 4 ）任何不等于零的数的零次幂为1.

请问当 $x$ 为何值时，代数式 ${(2 x + 3)}^{x + 2020}$ 的值为1.

查看试题解析

六、综合题

25.

(1)、若单项式 $x^{m - n} y^{14}$ 与单项式 $- \frac{1}{2} x^{3} y^{3 m - 8 n}$ 是一多项式中的同类项，求m、n的值；

(2)、先化简，再求值： $(\frac{x}{x + 1} + \frac{1}{x - 1}) \div \frac{1}{x^{2} - 1}$ ，其中 $x = \sqrt{2} - 1$ ．

查看试题解析
26. 本学期我们学习了“有理数乘方”运算，知道乘方的结果叫做“幂”，下面介绍一种有关“幂”的新运算.
定义： $a^{m}$ 与 $a^{n}$ （ $a \neq 0$ ， $m$ ， $n$ 都是正整数）叫做同底数幂，同底数幂除法记作 $a^{m} \div a^{n}$ .

运算法则如下： $a^{m} \div a^{n} = {\begin{array}{l} 当 m > n 时， a^{m} \div a^{n} = a^{m - n} \\ 当 m = n 时， a^{m} \div a^{n} = 1 \\ 当 m < n 时， a^{m} \div a^{n} = \frac{1}{a^{n - m}} \end{array}$

根据“同底数幂除法”的运算法则，回答下列问题：

(1)、填空： ${(\frac{1}{3})}^{3} \div {(\frac{1}{3})}^{2} =$ ， $5^{2} \div 5^{4} =$ ；

(2)、如果 $x > 0$ ，且 $2^{x} \div 2^{2 x} = \frac{1}{8}$ ，求出 $x$ 的值；

(3)、如果 ${(x - 2)}^{2 x + 2} \div {(x - 2)}^{12} = 1$ ，则 $x =$ .

查看试题解析
27. 阅读下列材料，解答下面的问题：
我们知道方程2x+3y=12有无数个解，但在实际生活中我们往往只需求出其正整数解．

例：由2x+3y=12，得：y= $\frac{12 - 2 x}{3}$ ，根据x、y为正整数，运用尝试法可以知道方程2x+3y=12的正整数解为 ${\begin{matrix} x = 3 \\ y = 2 \end{matrix}$ ．问题：

(1)、请你直接写出方程3x﹣y=6的一组正整数解．

(2)、若 $\frac{12}{x - 3}$ 为自然数，则满足条件的正整数x的值有（）个．

A、5 B、6 C、7 D、8

(3)、2020－2021学年七年级某班为了奖励学生学习的进步，购买单价为3元的笔记本与单价为5元的钢笔两种奖品，共花费48元，问有哪几种购买方案？

查看试题解析
28.

(1)、探索：如果 $\frac{2 x + 3}{x - 1} = 2 + \frac{m}{x - 1}$ ，则m=；如果 $\frac{3 x - 1}{x + 1} = 3 + \frac{m}{x + 1}$ 则m=；

(2)、总结：如果 $\frac{a x + b}{x + c} = a + \frac{m}{x + c}$ （其中a，b，c为常数），则m=；（用含a，b，c的式子表示）；

(3)、利用上述结论解决：若代数式 $\frac{4 x - 3}{x - 1}$ 的值为整数，求满足条件的整数x的值．

查看试题解析