北师大版备考2022中考数学二轮复习专题1 实数

试卷更新日期：2022-03-14 类型：二轮复习

进入出卷网下载

一、单选题

1. $\sqrt{81}$ 的算术平方根是（）

A、3 B、 $\pm 3$ C、 $\pm 9$ D、9

查看试题解析
2. 实数 $\frac{π}{4}$ ，0， $\sqrt[3]{27}$ ， $\sqrt{7}$ ， $\frac{\sqrt{16}}{2}$ ，0.1，-0.313313331…（每两个1之间依次增加一个3），其中无理数共有（）

A、2个 B、3个 C、4个 D、5个

查看试题解析
3. 下列式子变形正确的是（）

A、 $| π - 3 | = 3 - π$ B、 $- (a - 1) = - a - 1$ C、 $3 a - 5 a = - 2 a$ D、 $2 (a + b) = 2 a + b$

查看试题解析
4. 估计 $\sqrt{2} \times (\sqrt{14} - \sqrt{2})$ 的值在（）

A、2到3之间 B、3到4之间 C、4到5之间 D、5到6之间

查看试题解析
5. 如图是 5×5 的方格（每个小方格的边长为 1 个单位长度），图中阴影部分是正方形，则此正方形的边长为（）

A、5 B、 $\sqrt{13}$ C、 $\sqrt{7}$ D、3

查看试题解析
6. 如图．AB=AC，BD=1，BD⊥AD，则数轴上点C所表示的数为（）

A、 $\sqrt{5}$ +1 B、- $\sqrt{5}$ -1 C、- $\sqrt{5}$ +1 D、 $\sqrt{5}$ -1

查看试题解析
7. 实数a，b，c，d在数轴上的对应点的位置如图所示，则正确的结论是（）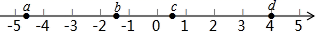

A、a＞﹣4 B、bd＞0 C、|a|＞|d| D、b+c＞0

查看试题解析
8. 下列计算或判断：（1）±3是27的立方根；（2） $\sqrt[3]{a^{3}} = a$ ；（3） $\sqrt{64}$ 的平方根是2；（4） $\sqrt[2]{{(\pm 8)}^{2}} = \pm 8$ ；（5） $\frac{1}{\sqrt{6} - \sqrt{5}} = \sqrt{6} + \sqrt{5}$ ，其中正确的有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
9. 比较大小错误的是（）

A、 $\sqrt{5}$ ＜ $\sqrt{7}$ B、 $\sqrt{35}$ ＋2＜ $\sqrt{82}$ ﹣1 C、 $\frac{- 7 - \sqrt{23}}{2}$ ＞﹣6 D、|1－ $\sqrt{3}$ |＞ $\sqrt{3}$ －1

查看试题解析
10. 一个数值转换器的原理如图所示，当输入的x为256时，输出的y是(　　)

A、16 B、 $\sqrt{2}$ C、 $\sqrt{3}$ D、 $\sqrt{8}$

查看试题解析

二、填空题

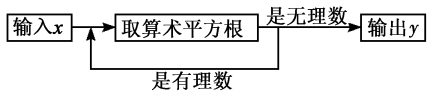11. 若 $^{3} \sqrt{a}$ =-5，则a= ．

查看试题解析
12. 若 $\sqrt{{(3 - x)}^{2}}$ =x-3成立，则x需满足条件：.

查看试题解析
13. 若m、n是两个连续的整数，且 $m < \sqrt{33} < n$ ，则 $m + n =$ .

查看试题解析
14. 比较大小： $\frac{\sqrt{5} - 1}{2}$ $\frac{1}{2}$ （填“＞”“＜”“＝”）.

查看试题解析
15. 已知：x-2的平方根是±2， $2 x + y + 7$ 的立方根为3，则 $x^{2} + y^{2}$ 的算术平方根为.

查看试题解析
16. 已知a是 $\sqrt{10}$ 的整数部分，b是它的小数部分，则 ${(- a)}^{3} + {(b + 3)}^{2}$ = ．

查看试题解析
17. 李明的作业本上有六道题：① $\sqrt[3]{- 2} = - \sqrt[3]{2}$ ，② $\sqrt{- 4} = - 2$ ，③ $\sqrt{{(- 2)}^{2}} = - 2$ ，④ $\sqrt{4} =$ ±2 ，⑤ $4 m^{- 2} = \frac{1}{4 m^{2}}$ ，⑥ $\sqrt{3 a} - \sqrt{2 a} = \sqrt{a}$ ，请你找出他做对的题是（填序号）.

查看试题解析
18. 小明学了在数轴上表示无理数的方法后，进行了练习：首先画数轴，原点为O，在数轴上找到表示数2的点A，然后过点A作AB⊥OA，使AB＝1；再以O为圆心，OB的长为半径作弧，交数轴正半轴于点P，那么点P表示的数是．

查看试题解析

三、计算题

19. 计算： $- 1^{0} - | \sqrt{7} - 3 | + \sqrt{28}$ .

查看试题解析
20. 计算： ${(- 1)}^{2022} + {(\frac{2}{3})}^{2} - {(π - 3.14)}^{0} - 3^{- 2}$

查看试题解析
21. 计算： $| - 2 | + \sqrt{9} + \frac{1}{2} \times \sqrt[3]{- 8}$ ．

查看试题解析
22. 计算： $2 c o s 30 ° - {(4 - π)}^{0} + t a n 60 ° - | - \sqrt{3} |$

查看试题解析

四、作图题

23. 如图所示，请在3×3的方格中，画出2个不同的正方形，要求满足以下条件：
①面积小于9；

②所画正方形的顶点都在格点上；

③边长是无理数，并写出边长.

边长为．边长为．

查看试题解析

五、解答题

24. 已知x+1的平方根是±2，2x+y﹣2的立方根是2，求x²+y²的算术平方根．

查看试题解析
25. 已知 $a + 1$ 的平方根是 $\pm 2$ ， $3 a + b - 1$ 的立方根是3，c是 $\sqrt{10}$ 的整数部分，求 $3 a + b - c$ 的平方根；

查看试题解析

六、综合题

26. 已知 $2 a - 7$ 和 $a + 4$ 是某正数的两个平方根， $b - 12$ 的立方根为-2.

(1)、求a，b的值；

(2)、求 $a + b$ 的平方根.

查看试题解析
27. 已知数a，b，c在数轴上的位置如图所示：
化简： $\sqrt{b^{2}} - | a - b | + \sqrt{{(c - a)}^{2}} - | c |$

查看试题解析
28. 材料1：因为无理数是无限不循环小数，所以无理数的小数部分我们不可能全部写出来.比如：π， $\sqrt{2}$ 等，而常用的“…”或者“≈”的表示方法都不够百分百准确.
材料2：2.5的整数部分是2，小数部分是0.5，小数部分可以看成是2.5−2得来的.

材料3：任何一个无理数，都夹在两个相邻的整数之间，如 $2 < \sqrt{5} < 3$ ，是因为 $\sqrt{4} < \sqrt{5} < \sqrt{9}$ .

根据上述材料，回答下列问题：

(1)、 $\sqrt{17}$ 的整数部分是，小数部分是.

(2)、 $5 + \sqrt{3}$ 也是夹在相邻两个整数之间的，可以表示为 $a < 5 + \sqrt{3} < b$ ，求 $a + b$ 的值.

(3)、已知 $3 + \sqrt{3} = x + y$ ，其中x是整数，且0＜y＜1，求x+4y的倒数.

查看试题解析