浙江省“七彩阳光”新高考研究联盟2020-2021学年高一下学期期中联考数学试题

试卷更新日期：2022-03-14 类型：期中考试

进入出卷网下载

一、单选题

1. 设复数z满足 $(3 + 4 i) z = | 3 - 4 i |$ （i为虚数单位），则 $z =$ （）

A、 $3 + 4 i$ B、 $3 - 4 i$ C、 $\frac{3}{5} + \frac{4}{5} i$ D、 $\frac{3}{5} - \frac{4}{5} i$

查看试题解析
2. 下列说法正确的是（）

A、直四棱柱是长方体 B、两个平面平行，其余各面是梯形的多面体是棱台 C、正棱锥的侧面是全等的等腰三角形 D、平行六面体不是棱柱

查看试题解析
3. 如图都是正方体的表面展开图，还原成正方体后，其中①、④处于正方体的两个相对面的是（）

A、（1）（2） B、（2）（3） C、（3）（4） D、（1）（4）

查看试题解析
4. 在 $△ A B C$ 中，内角A，B，C的对边分别为a，b，c，若 $a = 8 ， b = 7 ， A = \frac{π}{4}$ ，则 $△ A B C$ 的形状可能（）

A、锐角三角形 B、钝角三角形 C、钝角或锐角三角形 D、锐角、钝角或直角

查看试题解析
5. 已知向量 $\vec{a} ， \vec{b}$ 满足 $| \vec{a} | = 1 ， | \vec{b} | = \sqrt{3} ， | 2 \vec{a} + \vec{b} | = \sqrt{7}$ ，则 $\vec{b}$ 与 $\vec{b} - \vec{a}$ 的夹角为（）

A、30º B、60º C、120º D、150º

查看试题解析
6. 已知复数z满足 $2 \leq | z | \leq 3$ ，则 $| z - 1 - i |$ （i为虚数单位）的取值范围是（）

A、 $[2 - \sqrt{2} ， 2 + \sqrt{2}]$ B、 $[3 - \sqrt{2} ， 2 + \sqrt{2}]$ C、 $[3 - \sqrt{2} ， 3 + \sqrt{2}]$ D、 $[2 - \sqrt{2} ， 3 + \sqrt{2}]$

查看试题解析
7. 已知点P是边长为1的菱形 $A B C D$ 内一动点（包括边界）， $∠ D A B = 60 °$ ，则 $\vec{A P} \cdot \vec{A B}$ 的最大值为（）

A、 $\sqrt{3}$ B、 $\frac{3}{2}$ C、1 D、 $\frac{3}{4}$

查看试题解析
8. 已知向量 $\vec{a} ， \vec{b}$ 的夹角为 $\frac{π}{3}$ ， $| \vec{b} | = 2 | \vec{a} | = 2$ ，向量 $\vec{c} = x \vec{a} + y \vec{b}$ ，且 $x ， y \in [1 ， 2]$ ，则向量 $\vec{a} ， \vec{c}$ 夹角的余弦值的最小值为（）

A、 $\frac{\sqrt{21}}{7}$ B、 $\frac{2 \sqrt{7}}{7}$ C、 $\frac{\sqrt{3}}{2}$ D、 $\frac{3 \sqrt{21}}{14}$

查看试题解析

二、多选题

9. 已知函数 $f (x) = | l g x |$ ，则（）

A、 $f (x)$ 是偶函数 B、 $f (x)$ 值域为 $[0 ， + \infty)$ C、 $f (x)$ 在 $(0 ， + \infty)$ 上递增 D、 $f (x)$ 有一个零点

查看试题解析
10. 已知圆锥底面半径为3，高为4，则（）

A、圆锥的体积是 $36 π$ B、圆锥的侧面积是 $15 π$ C、圆锥的内切球体积是 $\frac{27}{2} π$ D、圆锥侧面展开图扇形的圆心角为 $\frac{6}{5} π$

查看试题解析
11. $△ A B C$ 中，内角A，B，C的对边分别为a，b，c，S为 $△ A B C$ 的面积，且 $a = 2$ ， $\vec{A B} \cdot \vec{A C} = 2 \sqrt{3} S$ ，下列选项正确的是（）

A、 $A = \frac{π}{3}$ B、若 $b = 3$ ，则 $△ A B C$ 有两解 C、若 $△ A B C$ 为锐角三角形，则b取值范围是 $(2 \sqrt{3} ， 4)$ D、若D为 $B C$ 边上的中点，则 $A D$ 的最大值为 $2 + \sqrt{3}$

查看试题解析
12. 已知等腰 $△ A B C$ 中 $∠ A = 120 ° ， A B = 4$ ， P为 $△ A B C$ 内部及边上的点，则 $\vec{P A} \cdot (\vec{P B} + \vec{P C})$ 的值可能是（）

A、-2 B、-3 C、24 D、16

查看试题解析

三、填空题

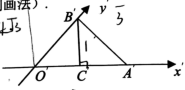
13. 已知函数 $f (x) = {\begin{array}{l} 2^{x} ， x \leq 0 ， \\ - \sqrt{x} ， x > 0 . \end{array}$ ，则 $f (f (1)) =$ ．

查看试题解析
14. 如图， $△ O^{'} A^{'} B^{'}$ 是水平放置的平面图形 $△ O A B$ 的直观图（斜二测画法）．若 $O^{'} A^{'} = 2 ， B^{'} C^{'} ⊥ O^{'} A^{'} ， B^{'} C^{'} = 1$ ，则原 $△ O A B$ 的面积是．

查看试题解析
15. 已知向量 $\vec{a} ， \vec{b}$ 满足 $| \vec{a} | = 3 ， \vec{a} \cdot \vec{b} = 6$ 若对任意实数x都有 $| \vec{a} - x \vec{b} | \geq | \vec{a} - \vec{b} |$ ，则 $| \vec{a} + λ \vec{b} | (λ \in R)$ 的最小值为．

查看试题解析
16. 已知 $△ A B C$ 的重心为G，内角A，B，C的对边分别为a，b，c，若 $\frac{\sqrt{3}}{3} a \vec{G A} + \frac{1}{2} b \vec{G B} + c \vec{G C} = \vec{0}$ ，则角A为．

查看试题解析

四、解答题

17. 已知复数 $z = m^{2} + m - (m + 1) i ， m \in R$ ， i为虚数单位．

(1)、当z是纯虚数时，求m的值；

(2)、当 $m = 1$ 时，求 $\frac{2 i}{z}$ ．

查看试题解析
18. 已知单位向量 $\vec{e_{1}} ， \vec{e_{2}}$ 的夹角为 $\frac{2}{3} π$ ，向量 $\vec{a} = 3 \vec{e_{1}} + \vec{e_{2}}$ ，向量 $\vec{b} = {\vec{e}}_{1} + λ \vec{e_{2}} (λ \in R)$ ．

(1)、若 $\vec{a} / / \vec{b}$ ，求 $λ$ 的值；

(2)、若 $\vec{a} ⊥ \vec{b}$ ，求 $| \vec{b} |$ 的值．

查看试题解析
19. 如图长方体 $A B C D - A_{1} B_{1} C_{1} D_{1}$ ，底面是边长为3的正方形，高为4，E为 $C C_{1}$ 的中点．

(1)、求长方体的表面积和它的外接球的表面积；

(2)、求三棱锥 $E - A_{1} B C$ 和长方体的体积之比．

查看试题解析
20. 某市需拍卖一块近似圆形的土地（如图），内接于圆的平面四边形 $A B C D$ 作为建筑用地，周边需做绿化．因地面限制，只能测量出 $A B = 1 k m ， A D = 2 k m$ ，测角仪测得角 $∠ B A D = 120 °$ ．

(1)、求 $B D$ 的长；

(2)、因地理条件限制， $A B ， A D$ 不能变更，但点C可以调整．建筑商为利益最大化，要求在弧上设计一点C使得四边形 $A B C D$ 面积最大，求四边形 $A B C D$ 面积的最大值．

查看试题解析
21. 如图，M，N分别是 $△ A B C$ 的边 $B C ， A B$ 上的点，且 $\vec{M C} = 2 \vec{B M} ， \vec{A N} = \frac{1}{2} \vec{A B}$ ， $A M$ 交 $C N$ 于点P．

(1)、若 $\vec{A M} = x \vec{A B} + y \vec{A C}$ ，求 $\frac{x}{y}$ 的值；

(2)、若 $A B = 3 ， A C = 4 ， ∠ B A C = 60 °$ ，求 $\vec{B P} \cdot \vec{B C}$ 的值．

查看试题解析
22. 已知向量 $\vec{m} = (s i n x ， 1) ， \vec{n} = (\sqrt{3} c o s x ， - \frac{1}{2})$ ．令函数 $f (x) = (\vec{m} + \vec{n}) \cdot \vec{m}$ ．

(1)、求函数 $f (x)$ 的最小正周期和单调递增区间；

(2)、 $△ A B C$ 中，内角A，B，C的对边分别为a，b，c， $∠ A C B$ 的角平分线交 $A B$ 于D．其中，函数 $f (C)$ 恰好为函数 $f (x)$ 的最大值，且此时 $C D = f (C)$ ，求 $3 a + b$ 的最小值．

查看试题解析