(人教版)2021-2022学年度第二学期人教版七年级数学第九章《不等式与不等式组》9.1不等式课堂练习卷
试卷更新日期:2022-03-14 类型:同步测试
一、单选题
-
1. 用不等式表示如图的解集,其中正确的是( )
 A、 B、 C、 D、2. 不等式3x≤6的解集,在数轴上表示正确的是( )A、
A、 B、 C、 D、2. 不等式3x≤6的解集,在数轴上表示正确的是( )A、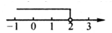 B、
B、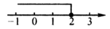 C、
C、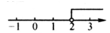 D、
D、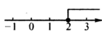 3. 在数轴上表示不等式的解集正确的是A、
3. 在数轴上表示不等式的解集正确的是A、 B、
B、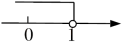 C、
C、 D、
D、 4. 已知 、 为常数,若 的解集是 ,则 的解集是A、 B、 C、 D、5. 下列实数中,不是x+4≥2的解的是( )A、﹣3 B、﹣2 C、0 D、3.56. 若 ,则下列式子一定成立的是( )A、 B、 C、 D、7. 如果a>b,那么下列结论一定正确的是( )A、a+3<b+3 B、a﹣3<b﹣3 C、3a>3b D、﹣3a>﹣3b8. 已知x<y,下列四个不等式中,正确的是( )A、-x<-y B、20-x>20-y C、x-19>y-19 D、-20x<-20y9. 已知 a,b都是实数,且a<b,则下列不等式的变形正确的是( )A、a-1>b-1 B、-a+2<-b+2 C、3a<3b D、10. 已知x>y,则下列不等式不成立的是( )A、﹣3x+6>﹣3y+6 B、2x>2y C、﹣3x<﹣3y D、x﹣6>y﹣6
4. 已知 、 为常数,若 的解集是 ,则 的解集是A、 B、 C、 D、5. 下列实数中,不是x+4≥2的解的是( )A、﹣3 B、﹣2 C、0 D、3.56. 若 ,则下列式子一定成立的是( )A、 B、 C、 D、7. 如果a>b,那么下列结论一定正确的是( )A、a+3<b+3 B、a﹣3<b﹣3 C、3a>3b D、﹣3a>﹣3b8. 已知x<y,下列四个不等式中,正确的是( )A、-x<-y B、20-x>20-y C、x-19>y-19 D、-20x<-20y9. 已知 a,b都是实数,且a<b,则下列不等式的变形正确的是( )A、a-1>b-1 B、-a+2<-b+2 C、3a<3b D、10. 已知x>y,则下列不等式不成立的是( )A、﹣3x+6>﹣3y+6 B、2x>2y C、﹣3x<﹣3y D、x﹣6>y﹣6二、填空题
-
11. 不等式(x-2)<3的解集是.12. 如图,关于x的不等式组在数轴上所表示的的解集是: .
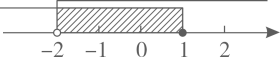 13. 请用不等式表示“x的2倍与3的和小于1”: .14. 根据“ 的2倍与3的差不小于8”列出的不等式是 .15. 已知 , ,则a的取值范围是.
13. 请用不等式表示“x的2倍与3的和小于1”: .14. 根据“ 的2倍与3的差不小于8”列出的不等式是 .15. 已知 , ,则a的取值范围是.三、解答题
-
16. 解不等式 < ,并把它的解集在数轴上表示出来.
 17. 解不等式 ,把它的解在数轴上表示出来,并写出该不等式的自然数解.18. 解不等式,并把解集在数轴上表示出来:(1)、2(x+1)-1≥3x+2;(2)、 ≥3(x-1)-4;19. 若方程(a+2)x=2的解为x=2想一想不等式(a+4)x>-3的解集是多少?试判断-2,-1,0,1,2,3这6个数中哪些数是该不等式的解。
17. 解不等式 ,把它的解在数轴上表示出来,并写出该不等式的自然数解.18. 解不等式,并把解集在数轴上表示出来:(1)、2(x+1)-1≥3x+2;(2)、 ≥3(x-1)-4;19. 若方程(a+2)x=2的解为x=2想一想不等式(a+4)x>-3的解集是多少?试判断-2,-1,0,1,2,3这6个数中哪些数是该不等式的解。
20. 某数学兴趣小组在学习“不等式的性质”时,有两名同学的对话如下: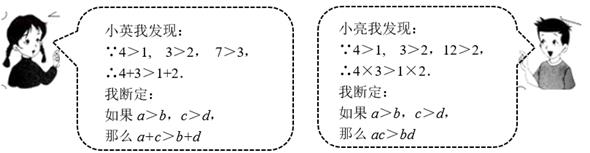
你认为小英和小亮的结论正确吗?如果正确,请说明理由;如果不正确,请举出一个反例。
21. 现有不等式的两个性质:①在不等式的两边都加上(或减去)同一个整式,不等号的方向不变;
②在不等式的两边都乘以同一个数(或整式),乘的数(或整式)为正时不等号的方向不变,乘的数(或整式)为负时不等号的方向改变.
请解决以下两个问题:
(1)、利用性质①比较2a与a的大小(a≠0);(2)、利用性质②比较2a与a的大小(a≠0).22. 【提出问题】已知x﹣y=2,且x>1,y<0,试确定x+y的取值范围.【分析问题】先根据已知条件用一个量如取y表示另一个量如x,然后根据题中已知量x的取值范围,构建另一个量y的不等式,从而确定该量y的取值范围,同法再确定另一未知量x的取值范围,最后利用不等式性质即可获解.
【解决问题】解:∵x﹣y=2,∴x=y+2.
又∵x>1,∴y+2>1,∴y>﹣1.
又∵y<0,∴﹣1<y<0,…①
同理得1<x<2…②
由①+②得﹣1+1<y+x<0+2.
∴x+y的取值范围是0<x+y<2.
【尝试应用】已知x﹣y=﹣3,且x<﹣1,y>1,求x+y的取值范围.