2021-2022学年浙教版数学八下第六章 反比例函数 单元检测卷
试卷更新日期:2022-03-12 类型:单元试卷
一、单选题
-
1. 下列函数中,属于反比例函数的是( )A、 B、 C、 D、2. 给出下列函数:① ;② ;③ ;④ ,其中 随 的增大而减小的函数的个数为( )A、1 B、2 C、3 D、43. 若反比例函数 的图象经过点 ,则此反比例函数的图象在( )A、第三、四象限 B、第二、四象限 C、第一、二象限 D、第一、三象限4. 已知 ,则函数 和 的图象大致是( )A、
 B、
B、 C、
C、 D、
D、 5. 在反比例函数 的每一条曲线上, 都随着 的增大而减小,则 的值可以是( )A、8 B、7 C、5 D、36. 如图所示,反比例函数 的图象经过矩形OABC的边AB的中点 ,则矩形OABC的面积为( )
5. 在反比例函数 的每一条曲线上, 都随着 的增大而减小,则 的值可以是( )A、8 B、7 C、5 D、36. 如图所示,反比例函数 的图象经过矩形OABC的边AB的中点 ,则矩形OABC的面积为( ) A、2 B、4 C、5 D、87. 关于反比例函数y=﹣ ,下列叙述正确的是( )A、函数图象经过点(﹣2,﹣3) B、函数图象在第一、三象限 C、当x>﹣2时,y>3 D、当x<0时,y随x的增大而增大8. 如图,反比例函数y= 的图象与直线y=mx相交于A , B两点,点B的坐标为(﹣2,﹣3),则点A的坐标为( ).
A、2 B、4 C、5 D、87. 关于反比例函数y=﹣ ,下列叙述正确的是( )A、函数图象经过点(﹣2,﹣3) B、函数图象在第一、三象限 C、当x>﹣2时,y>3 D、当x<0时,y随x的增大而增大8. 如图,反比例函数y= 的图象与直线y=mx相交于A , B两点,点B的坐标为(﹣2,﹣3),则点A的坐标为( ). A、(﹣2,﹣3) B、(2,3) C、(﹣2,3) D、(2,﹣3)9. 如图,一次函数 的图象与反比例函数 ( 为常数且 )的图象都经过 ,结合图象,则不等式 的解集是( )
A、(﹣2,﹣3) B、(2,3) C、(﹣2,3) D、(2,﹣3)9. 如图,一次函数 的图象与反比例函数 ( 为常数且 )的图象都经过 ,结合图象,则不等式 的解集是( )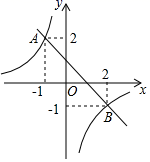 A、 B、 C、 或 D、 或10. 如图,直线 与 轴、 轴相交于 , 两点,与 的图象相交于 , 两点,连接 , .下列结论:① ;②不等式 的解集是 或 ;③ ;④ .其中正确的结论是( )
A、 B、 C、 或 D、 或10. 如图,直线 与 轴、 轴相交于 , 两点,与 的图象相交于 , 两点,连接 , .下列结论:① ;②不等式 的解集是 或 ;③ ;④ .其中正确的结论是( )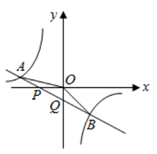 A、①③ B、②③④ C、①③④ D、②④
A、①③ B、②③④ C、①③④ D、②④二、填空题
-
11. 反比例函数 中自变量x的取值范围是。12. 设函数 与y=x﹣1的图象的交点坐标为(a,b),则 的值为.13. 一次函数y=-x+1与反比例函数 (k<0)中,x与y的部分对应值如下表:
x
-3
-2
-1
1
2
3
y=-x+1
4
3
2
0
-1
-2
1
2
-2
-1
-
则不等式 >0的解集为.
14. 已知反比例函数图象经过点(-1,4),(m,2),那么m=.15. 如图所示,在平面直角坐标系中,菱形OABC的面积为12,点 在 轴上,点 在反比例函数 的图象上,则 的值为. 16. 若 与 成反比例关系, 与 成反比例关系,则 与 成关系.
16. 若 与 成反比例关系, 与 成反比例关系,则 与 成关系.三、解答题
-
17. 已知正比例函数 与反比例函数交于A(-2,a),求这个反比例函数的解析式。18. 某市为促进经济发展,增强对外贸易的竞争力,把距离港口360千米的普通公路升级成了同等长度的高速公路,结果汽车行驶的平均速度比原来提高了50%,行驶时间缩短了2小时,求汽车原来的平均速度.19. 如图,在平面直角坐标系xOy中,反比例函数y= 的图象与一次函数y=-x+1的图象的一个交点为A(-1,m).
 (1)、求这个反比例函数的表达式;(2)、如果一次函数y=-x+1的图象与x轴交于点B(n,0),请确定当x<n时,对应的反比例函数y= 的值的范围.20. 如图,在Rt△AOB中,∠ABO=90°,OB=4,AB=8,且反比例函数 在第一象限内的图象分别交OA、AB于点C和点D,连结OD,若S△BOD=4,请回答下列问题:
(1)、求这个反比例函数的表达式;(2)、如果一次函数y=-x+1的图象与x轴交于点B(n,0),请确定当x<n时,对应的反比例函数y= 的值的范围.20. 如图,在Rt△AOB中,∠ABO=90°,OB=4,AB=8,且反比例函数 在第一象限内的图象分别交OA、AB于点C和点D,连结OD,若S△BOD=4,请回答下列问题: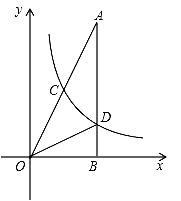 (1)、求反比例函数解析式;(2)、求C点坐标.21. 小林为探索函数 的图象与性质经历了如下过程.
(1)、求反比例函数解析式;(2)、求C点坐标.21. 小林为探索函数 的图象与性质经历了如下过程. (1)、列表:根据表中 的取值,求出对应的 值,将空白处填写完整.
(1)、列表:根据表中 的取值,求出对应的 值,将空白处填写完整.x
…
2.5
3
3.5
4
4.5
5
…
y
…
6
2
1.2
1
…
(2)、以表中各组对应值为点的坐标,在平面直角坐标系中描点并画出函数图象.(3)、若函数 的图象与 的图象交于点 ,且 为正整数),则 的值是22. 已知反比例函数 (k 为常数且 k≠0) 的图象经过点 .(1)、求这个函数的表达式;(2)、当 时,直接写出 y 的取值范围;(3)、判断点 是否在这个函数的图象上,并说明理由.23. 定义:只有三边相等的四边形称为准菱形.
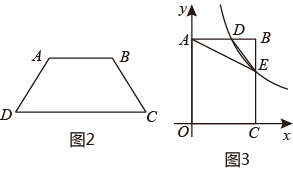 (1)、如图1,图形 (填序号)是准菱形;(2)、如图2,四边形ABCD中,AB∥DC,∠B+∠D=180°,AB=AD,求证:四边形ABCD是准菱形;(3)、如图3,在平面直角坐标系xOy中,矩形OABC的边OA,OC分别落在y轴,x轴上,反比例函数y= (k>0)的图象分别与边AB,BC交于点D,E.已知AD=DE,△ADE的面积为10,AD:DB=5:3,若点F是坐标平面上一点,四边形ADEF是准菱形,当准菱形ADEF面积最大时,求点F的坐标.24. 如图,在矩形ABCD中,AD=5,AB=3,E是BC上一点(不包括B,C两端点),连结AE和DE,作DF⊥AE于点F.
(1)、如图1,图形 (填序号)是准菱形;(2)、如图2,四边形ABCD中,AB∥DC,∠B+∠D=180°,AB=AD,求证:四边形ABCD是准菱形;(3)、如图3,在平面直角坐标系xOy中,矩形OABC的边OA,OC分别落在y轴,x轴上,反比例函数y= (k>0)的图象分别与边AB,BC交于点D,E.已知AD=DE,△ADE的面积为10,AD:DB=5:3,若点F是坐标平面上一点,四边形ADEF是准菱形,当准菱形ADEF面积最大时,求点F的坐标.24. 如图,在矩形ABCD中,AD=5,AB=3,E是BC上一点(不包括B,C两端点),连结AE和DE,作DF⊥AE于点F.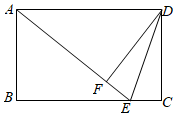 (1)、若AE=AD,求证:△ADF≌△EAB;(2)、在(1)条件下,求△DEF的面积;(3)、设AE=x,DF=y,请求y关于x的函数关系式及自变量x的取值范围.
(1)、若AE=AD,求证:△ADF≌△EAB;(2)、在(1)条件下,求△DEF的面积;(3)、设AE=x,DF=y,请求y关于x的函数关系式及自变量x的取值范围.