2021-2022学年浙教版数学八下6.3 反比例函数的应用 同步练习
试卷更新日期:2022-03-11 类型:同步测试
一、单选题
-
1. 某工厂现有原材料100吨,每天平均用去x吨,这批原材料能用y天,则y与x之间的函数表达式为( )A、 B、 C、 D、2. 反比例函数 和正比例函数 的图象如图所示.由此可以得到方程 的实数根为( )
 A、 B、 C、 D、3. 如果正比例函数图象与反比例函数图象的一个交点的坐标为(3,-4),那么另一个交点的坐标为( )A、(-3,-4) B、(3,4) C、(−3,4) D、(-4,3)4. 已知点A(x1 , y1)在反比例函数y1= 的图象上,点B(x2 , y2)在一次函数y2=kx﹣k的图象上,当k>0时,下列判断中正确的是( )A、当x1=x2>2时,y1>y2 B、当x1=x2<2时,y1>y2 C、当y1=y2>k时,x1<x2 D、当y1=y2<k时,x1>x25. 如图,点 落在第二象限内双曲线 上,过 两点分别作 轴的垂线段,垂足为 ,连接 ,若 且 ,则 的值为( )
A、 B、 C、 D、3. 如果正比例函数图象与反比例函数图象的一个交点的坐标为(3,-4),那么另一个交点的坐标为( )A、(-3,-4) B、(3,4) C、(−3,4) D、(-4,3)4. 已知点A(x1 , y1)在反比例函数y1= 的图象上,点B(x2 , y2)在一次函数y2=kx﹣k的图象上,当k>0时,下列判断中正确的是( )A、当x1=x2>2时,y1>y2 B、当x1=x2<2时,y1>y2 C、当y1=y2>k时,x1<x2 D、当y1=y2<k时,x1>x25. 如图,点 落在第二象限内双曲线 上,过 两点分别作 轴的垂线段,垂足为 ,连接 ,若 且 ,则 的值为( ) A、4 B、-4 C、2 D、-26. 设双曲线 (k > 0)与直线y=x交于A,B两点(点A在第三象限),将双曲线在第一象限的一支沿射线BA的方向平移,使其经过点A,将双曲线在第三象限的一支沿射线AB的方向平移,使其经过点B,平移后的两条曲线相交于点P,Q两点,此时我们称平移后的两条曲线所围部分(如图中阴影部分)为双曲线的“眸”,PQ为双曲线的“眸径”.当双曲线 (k > 0)的眸径为4时,k的值为( )
A、4 B、-4 C、2 D、-26. 设双曲线 (k > 0)与直线y=x交于A,B两点(点A在第三象限),将双曲线在第一象限的一支沿射线BA的方向平移,使其经过点A,将双曲线在第三象限的一支沿射线AB的方向平移,使其经过点B,平移后的两条曲线相交于点P,Q两点,此时我们称平移后的两条曲线所围部分(如图中阴影部分)为双曲线的“眸”,PQ为双曲线的“眸径”.当双曲线 (k > 0)的眸径为4时,k的值为( )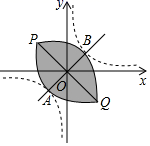 A、 B、 C、2 D、47. 如图,在直角坐标系中,直线 的图象上有8个点,从左往右依次记为 , ,…, (横坐标依次增加2个单位),要使这些点平均分布在函数 的图象两侧,每侧4个点,则 可以取到的整数值有( )
A、 B、 C、2 D、47. 如图,在直角坐标系中,直线 的图象上有8个点,从左往右依次记为 , ,…, (横坐标依次增加2个单位),要使这些点平均分布在函数 的图象两侧,每侧4个点,则 可以取到的整数值有( ) A、7个 B、8个 C、9个 D、10个8. 如图是一个闭合电路,其电源的电压为定值,电流I(A)是电阻R()的反比例函数.当时, . 若电阻R增大 , 则电源I为( )
A、7个 B、8个 C、9个 D、10个8. 如图是一个闭合电路,其电源的电压为定值,电流I(A)是电阻R()的反比例函数.当时, . 若电阻R增大 , 则电源I为( ) A、3A B、4A C、7A D、12A9. 市一小学数学课外兴趣小组的同学每人制作一个面积为200cm2的矩形学具进行展示,设矩形的宽为xcm,长为ycm,那么这些同学所制作的矩形长y(cm)与宽x(cm)之间的函数关系的图象大致是( )A、
A、3A B、4A C、7A D、12A9. 市一小学数学课外兴趣小组的同学每人制作一个面积为200cm2的矩形学具进行展示,设矩形的宽为xcm,长为ycm,那么这些同学所制作的矩形长y(cm)与宽x(cm)之间的函数关系的图象大致是( )A、 B、
B、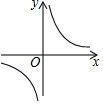 C、
C、 D、
D、 10. 验光师测得一组关于近视眼镜的度数y(度)与镜片焦距x(米)的对应数据如下表.根据表中数据,可得y关于x的函数表达式为
10. 验光师测得一组关于近视眼镜的度数y(度)与镜片焦距x(米)的对应数据如下表.根据表中数据,可得y关于x的函数表达式为近视眼镜的度数y(度)
200
250
400
500
1000
镜片焦距x(米)
0.50
0.40
0.25
0.20
0.10
A、 B、 C、 D、二、填空题
-
11. 表1给出了正比例函数 的图象上部分点的坐标,表2给出了反比例函数 的图象上部分点的坐标.
表1
x
0
1
2
3
y1
0
-2
-4
-6
表2
x
0.5
1
2
4
y2
-4
-2
-1
-0.5
则当 时, 的值为.
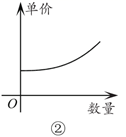
12. 正比例函数y1=k1x(k1≠0)与反比例函数y2= (k2≠0)的图象的一个交点是M(﹣3,2),若y2<y1 , 则x的取值范围是.13. 如图,在平面直角坐标系中,函数 与 的图象交于A、B两点,过点A作 轴的垂线,交函数 的图象于点C,连接BC,则△ABC的面积为.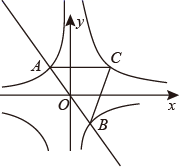 14. 一货轮从甲港往乙港运送货物,甲港的装货速度是每小时30吨,一共装了8小时,到达乙港后开始卸货,乙港卸货的速度是每小时x吨,设卸货的时间是y小时,则y与x之间的函数关系式是 (不必写自变量取值范围).15. 已知近视眼镜的度数D(度)与镜片焦距f(米)成反比例关系,且400度近视眼镜镜片的焦距为0.25米.小慧原来戴400度的近视眼镜,经过一段时间的矫正治疗后,现在只需戴镜片焦距为0.4米的眼镜了,则小慧所戴眼镜的度数降低了 度.16. 经济学家在硏究市场供求关系时,一般用纵轴表示产品单价(自变量),而用横轴表示产品数量(因变量),下列两条曲线分别表示某种产品数量与单价之间的供求关系,一条表示厂商希望的供应曲线,另一条表示客户希望的需求曲线,其中表示客户希望的需求曲线的是(填入序号即可).
14. 一货轮从甲港往乙港运送货物,甲港的装货速度是每小时30吨,一共装了8小时,到达乙港后开始卸货,乙港卸货的速度是每小时x吨,设卸货的时间是y小时,则y与x之间的函数关系式是 (不必写自变量取值范围).15. 已知近视眼镜的度数D(度)与镜片焦距f(米)成反比例关系,且400度近视眼镜镜片的焦距为0.25米.小慧原来戴400度的近视眼镜,经过一段时间的矫正治疗后,现在只需戴镜片焦距为0.4米的眼镜了,则小慧所戴眼镜的度数降低了 度.16. 经济学家在硏究市场供求关系时,一般用纵轴表示产品单价(自变量),而用横轴表示产品数量(因变量),下列两条曲线分别表示某种产品数量与单价之间的供求关系,一条表示厂商希望的供应曲线,另一条表示客户希望的需求曲线,其中表示客户希望的需求曲线的是(填入序号即可).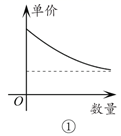
三、解答题
-
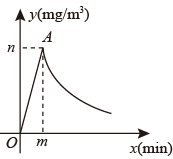
17. 为了做好校园疫情防控工作,学校后勤每天对全校办公室和教室进行药物喷洒消毒,完成1间教室的药物喷洒要5min , 药物喷洒时教室内空气中的药物浓度 (单位: )与时间 (单位:min)的函数关系式为 ,其图象为图中线段 ,药物喷洒完成后 与 成反比例函数关系,两个函数图象的交点为 ,当教室空气中的药物浓度不高于 时,对人体健康无危害,如果后勤人员依次对一班至十一班教室(共11间)进行药物喷洒消毒当最后一间教室药物喷洒完成后,一班能否能让人进入教室?请通过计算说明.
 18. 如图,在平面直角坐标系中,正比例函数 与函数 的图象相交于点 , 轴于点B.平移直线 ,使其经过点B,得到直线l,求直线l所对应的函数表达式.
18. 如图,在平面直角坐标系中,正比例函数 与函数 的图象相交于点 , 轴于点B.平移直线 ,使其经过点B,得到直线l,求直线l所对应的函数表达式. 19. 某市某蔬菜生产基地在气温较低时,用装有恒温系统的大棚栽培一种在温度为 的条件下生长最快的新品种,下图是某天恒温系统从开启到关闭及关闭后,大棚里温度 随时间x(h)变化的函数图象,其中AB段是恒温阶段,BC段是双曲线 的一部分,请根据图中信息解答下列问题.
19. 某市某蔬菜生产基地在气温较低时,用装有恒温系统的大棚栽培一种在温度为 的条件下生长最快的新品种,下图是某天恒温系统从开启到关闭及关闭后,大棚里温度 随时间x(h)变化的函数图象,其中AB段是恒温阶段,BC段是双曲线 的一部分,请根据图中信息解答下列问题. (1)、恒温系统在这天保持大棚内温度为 的时间有多少小时?(2)、求 的值.(3)、恒温系统在一天24h内保持大棚温度在 的时间有多少小时?20. 如图是某游乐园“水上滑梯”的侧面示意图,其中BD段可看成双曲线 的一部分,矩形OABC是向上攀爬的阶梯部分.以O为中心建立平面直角坐标系,使点A和点C分别落在x轴和y轴的正半轴上.已知OC=5米,入口平台BC=1.8米,滑梯的出口D点到水面的距离DE为0.75米(O、A、E在一条直线上).求B、D之间的水平距离AE的长.
(1)、恒温系统在这天保持大棚内温度为 的时间有多少小时?(2)、求 的值.(3)、恒温系统在一天24h内保持大棚温度在 的时间有多少小时?20. 如图是某游乐园“水上滑梯”的侧面示意图,其中BD段可看成双曲线 的一部分,矩形OABC是向上攀爬的阶梯部分.以O为中心建立平面直角坐标系,使点A和点C分别落在x轴和y轴的正半轴上.已知OC=5米,入口平台BC=1.8米,滑梯的出口D点到水面的距离DE为0.75米(O、A、E在一条直线上).求B、D之间的水平距离AE的长.
四、综合题
-
21. 甲、乙两名实验者在A、B两个实验室进行空调制冷后舒适度测试,两人同时启动空调1小时后,开始记录数据,经过数据分析,甲的舒适指数与空调启动时间成反比例关系,乙的舒适指数与空调启动时间的函数关系式为 , 函数图象如图所示且在2小时,乙的舒适指数最大.
 (1)、求m、k;(2)、当时,求的较大值;(3)、若规定舒适度小于1时,实验室则不适合人长时间逗留,求至少启动空调多少小时后,两个实验室均不适合人长时间逗留.22. 某科技有限公司成功研制出一种市场急需的电子产品,已于当年投入生产并进行销售,已知生产这种电子产品的成本为4元/件,在销售过程中发现:每年的年销售量y(万件)与销售价格x(元/件)的关系如图,其中AB段为反比例函数图象的一部分,设公司销售这种电子产品的年利润为w(万元).
(1)、求m、k;(2)、当时,求的较大值;(3)、若规定舒适度小于1时,实验室则不适合人长时间逗留,求至少启动空调多少小时后,两个实验室均不适合人长时间逗留.22. 某科技有限公司成功研制出一种市场急需的电子产品,已于当年投入生产并进行销售,已知生产这种电子产品的成本为4元/件,在销售过程中发现:每年的年销售量y(万件)与销售价格x(元/件)的关系如图,其中AB段为反比例函数图象的一部分,设公司销售这种电子产品的年利润为w(万元). (1)、请求出y(万件)与x(元/件)之间的函数关系式;
(1)、请求出y(万件)与x(元/件)之间的函数关系式;①求出当4≤x≤8时的函数关系式;
②求出当8<x≤28时的函数关系式.
(2)、求出这种电子产品的年利润w(万元)与x(元/件)之间的函数关系式;(3)、求出年利润的最大值.23. 某玩具厂生产一种玩具,本着控制固定成本,降价促销的原则,使生产的玩具能够全部售出.据市场调查,若按每个玩具280元销售时,每月可销售300个.若销售单价每降低1元,每月可多售出2个.据统计,每个玩具的固定成本Q(元)与月产销量y(个)满足如下关系:月产销量y(个)
…
160
200
240
300
…
每个玩具的固定成本Q(元)
…
60
48
40
32
…
(1)、每月产销量y(个)与销售单价x(元)之间的函数关系式为 ▲ ;从上表可知.每个玩具的固定成本Q(元)与月产销量y(个)之间满足反比例函数关系式,求出Q与y之间的关系式;(2)、若每个玩具的固定成本为30元,求它的销售单价是多少元?(3)、若该厂这种玩具的月产销量不超过400个,求此时销售单价是多少元?24. 电子体重科读数直观又便于携带,为人们带来了方便.某综合实践活动小组设计了简易电子体重秤:制作一个装有踏板(踏板质量忽略不计)的可变电阻R1 , R1与踏板上人的质量m之间的函数关系式为R1=km+b(其中k,b为常数,0≤m≤120),其图象如图1所示;图2的电路中,电源电压恒为8伏,定值电阻R0的阻值为30欧,接通开关,人站上踏板,电压表显示的读数为U0 , 该读数可以换算为人的质量m,温馨提示:①导体两端的电压U,导体的电阻R,通过导体的电流I,满足关系式I= ;
②串联电路中电流处处相等,各电阻两端的电压之和等于总电压.
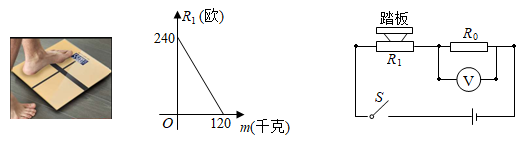 (1)、求k,b的值;(2)、求R1关于U0的函数解析式;(3)、用含U0的代数式表示m;(4)、若电压表量程为0~6伏,为保护电压表,请确定该电子体重秤可称的最大质量.
(1)、求k,b的值;(2)、求R1关于U0的函数解析式;(3)、用含U0的代数式表示m;(4)、若电压表量程为0~6伏,为保护电压表,请确定该电子体重秤可称的最大质量.