2021-2022学年浙教版数学八下6.2 反比例函数的图象和性质 同步练习
试卷更新日期:2022-03-11 类型:同步测试
一、单选题
-
1. 若点 在反比例函数 的图象上,则 的值是( )A、-6 B、-2 C、2 D、62. 下列各点中,在正比例函数 的图象上的是( )A、 B、(﹣3,﹣1) C、(0,1) D、(6,3)3. 已知电压 、电流 、电阻 三者之间的关系式为 或 .实际生活中,由于给定已知量不同,因此会有不同的图象,图象不可能是( )A、
 B、
B、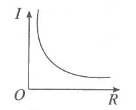 C、
C、 D、
D、 4. 以正方形ABCD两条对角线的交点 为坐标原点,建立如图所示的平面直角坐标系,双曲线 经过点 ,则正方形ABCD的面积是( )
4. 以正方形ABCD两条对角线的交点 为坐标原点,建立如图所示的平面直角坐标系,双曲线 经过点 ,则正方形ABCD的面积是( ) A、6 B、12 C、14 D、155. 已知反比例函数 的图象,在每一象限内, 的值随 值的增大而减小,则一次函数 的图象不经过( )A、第一象限 B、第二象限 C、第三象限 D、第四象限6. 如图,在平面直角坐标系中, 是 轴正半轴上的一个定点,点 是反比例函数 图象上的一个动点, 轴于点 .当点 的横坐标逐渐增大时,四边形OAPB的面积将会( )
A、6 B、12 C、14 D、155. 已知反比例函数 的图象,在每一象限内, 的值随 值的增大而减小,则一次函数 的图象不经过( )A、第一象限 B、第二象限 C、第三象限 D、第四象限6. 如图,在平面直角坐标系中, 是 轴正半轴上的一个定点,点 是反比例函数 图象上的一个动点, 轴于点 .当点 的横坐标逐渐增大时,四边形OAPB的面积将会( ) A、逐渐增大 B、不变 C、逐渐减小 D、先增大后减小7. 如图所示,在平面直角坐标系xOy中,点A、B、C为反比例函数y=(k>0)上不同的三点,连接OA、OB、OC,过点A作AD⊥y轴于点D,过点B、C分别作BE,CF垂直x轴于点E、F,OC与BE相交于点M,记△AOD、△BOM、四边形CMEF的面积分别为S1、S2、S3 , 则( )
A、逐渐增大 B、不变 C、逐渐减小 D、先增大后减小7. 如图所示,在平面直角坐标系xOy中,点A、B、C为反比例函数y=(k>0)上不同的三点,连接OA、OB、OC,过点A作AD⊥y轴于点D,过点B、C分别作BE,CF垂直x轴于点E、F,OC与BE相交于点M,记△AOD、△BOM、四边形CMEF的面积分别为S1、S2、S3 , 则( )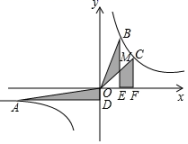 A、S1=S2+S3 B、S2=S3 C、S3>S2>S1 D、S1S2<S328. 在反比例函数y=的图像上有三点A1(x1 , y1)、A2(x2 , y2)、A3(x3 , y3),已知x1< x2<0<x3则下列各式中,正确的是( )A、y1<y2<y3 B、y3< y2< y1 C、y2< y1< y3 D、y3< y1< y29. 已知函数中,在每个象限内,的值随的值增大而增大,那么它和函数在同一直角坐标平面内的大致图像是( ).A、
A、S1=S2+S3 B、S2=S3 C、S3>S2>S1 D、S1S2<S328. 在反比例函数y=的图像上有三点A1(x1 , y1)、A2(x2 , y2)、A3(x3 , y3),已知x1< x2<0<x3则下列各式中,正确的是( )A、y1<y2<y3 B、y3< y2< y1 C、y2< y1< y3 D、y3< y1< y29. 已知函数中,在每个象限内,的值随的值增大而增大,那么它和函数在同一直角坐标平面内的大致图像是( ).A、 B、
B、 C、
C、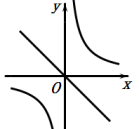 D、
D、 10. y= x,下列结论正确的是( )A、函数图象必经过点(1,2) B、函数图象必经过第二、四象限 C、不论x取何值,总有y>0 D、y随x的增大而增大
10. y= x,下列结论正确的是( )A、函数图象必经过点(1,2) B、函数图象必经过第二、四象限 C、不论x取何值,总有y>0 D、y随x的增大而增大二、填空题
-
11. 老师给出一个函数,甲、乙、丙、丁四位同学分别指出了这个函数的一个性质.
甲:函数图象不经过第二象限;
乙:函数图象上两个点 且
丙:函数图象在第一象限;
丁:在自变量取值范围内,y随x的增大而减小.老师说这四位同学的叙述都是正确的,请你构造一个满足上述性质的函数
12. 如图所示,在平面直角坐标系中,函数 的图象经过 两点,过点 作 轴的垂线,垂足为点 ,连结AB,BC.若 的面积为3,则点 的坐标为.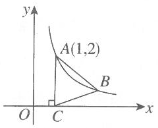 13. 若、两点都在函数的图像上,且< , 则k的取值范围是 .14. 如图,直线AB与x轴交于点 , 与x轴夹角为30°,将沿直线AB翻折,点O的对应点C恰好落在双曲线上,则k的值为 .
13. 若、两点都在函数的图像上,且< , 则k的取值范围是 .14. 如图,直线AB与x轴交于点 , 与x轴夹角为30°,将沿直线AB翻折,点O的对应点C恰好落在双曲线上,则k的值为 . 15. 如图,在平面直角坐标系中,C为y轴正半轴上一点,过点C作直线AB∥x轴,直线分别与反比例函数y 和y 的图象交于A、B两点,连结AO和BO.若S△AOB=3,则k的值为 .
15. 如图,在平面直角坐标系中,C为y轴正半轴上一点,过点C作直线AB∥x轴,直线分别与反比例函数y 和y 的图象交于A、B两点,连结AO和BO.若S△AOB=3,则k的值为 . 16. 如图,在平面直角坐标系中,矩形ABCD的BC边落在y轴上,其他部分均在第二象限,双曲线y= 过点A,延长对角线CA交x轴于点E,以AD、AE为边作平行四边形AEFD,若平行四边形AEFD的面积为2,则k的值为.
16. 如图,在平面直角坐标系中,矩形ABCD的BC边落在y轴上,其他部分均在第二象限,双曲线y= 过点A,延长对角线CA交x轴于点E,以AD、AE为边作平行四边形AEFD,若平行四边形AEFD的面积为2,则k的值为.
三、解答题
-
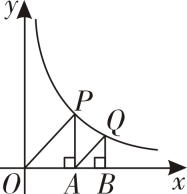
17. 如图,△OAP、△ABQ是等腰直角三角形,点P、Q在函数 (k≠0)第一象限的图像上,直角顶点A、B均在x轴上,若OA=3,求点Q的坐标.
 18. 已知y=y1﹣y2 , y1与x2成正比例,y2与x+3成反比例,当x=0时,y=2;当x=2时,y=0,求y与x的函数关系式,并指出自变量的取值范围.19. 小明家饮水机中原有水的温度为20℃,通电开机后,饮水机自动开始加热[此过程中水温y(℃)与开机时间x(分)满足一次函数关系],当加热到100℃时自动停止加热,随后水温开始下降[此过程中水温y(℃)与开机时间x(分)成反比例关系],当水温降至20℃时,饮水机又自动开始加热…,重复上述程序(如图所示),根据图中提供的信息,解答下列问题:
18. 已知y=y1﹣y2 , y1与x2成正比例,y2与x+3成反比例,当x=0时,y=2;当x=2时,y=0,求y与x的函数关系式,并指出自变量的取值范围.19. 小明家饮水机中原有水的温度为20℃,通电开机后,饮水机自动开始加热[此过程中水温y(℃)与开机时间x(分)满足一次函数关系],当加热到100℃时自动停止加热,随后水温开始下降[此过程中水温y(℃)与开机时间x(分)成反比例关系],当水温降至20℃时,饮水机又自动开始加热…,重复上述程序(如图所示),根据图中提供的信息,解答下列问题:(Ⅰ)当0≤x≤8时,求水温y(℃)与开机时间x(分)的函数关系式;
(Ⅱ)求图中t的值;
(Ⅲ)若小明在通电开机后即外出散步,请你预测小明散步45分钟回到家时,饮水机内的温度约为多少℃?
 20. 如图,D为反比例函数 的图象上一点,过D作DE⊥ 轴于点E,DC⊥ 轴于点C,一次函数 的图象经过C点,与 轴相交于A点,四边形DCAE的面积为4,求 的值.
20. 如图,D为反比例函数 的图象上一点,过D作DE⊥ 轴于点E,DC⊥ 轴于点C,一次函数 的图象经过C点,与 轴相交于A点,四边形DCAE的面积为4,求 的值.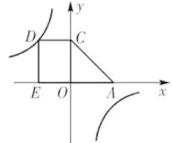 21. 如图所示,线段OA与反比例函数 在第一象限的图象相交于点 B(4,3),B 是OA的中点,AC∥x 轴交反比例函数图象于点 C .
21. 如图所示,线段OA与反比例函数 在第一象限的图象相交于点 B(4,3),B 是OA的中点,AC∥x 轴交反比例函数图象于点 C . (1)、求 的值;(2)、求AC的长.22. 如图,在平面直角坐标系内,双曲线上有A,B两点,且与直线交于第一象限内的点A,点A的坐标为 , 点B的坐标为 , 过点B作y轴的平行线,交x轴于点C,交直线与点D.
(1)、求 的值;(2)、求AC的长.22. 如图,在平面直角坐标系内,双曲线上有A,B两点,且与直线交于第一象限内的点A,点A的坐标为 , 点B的坐标为 , 过点B作y轴的平行线,交x轴于点C,交直线与点D. (1)、求:点D的坐标;(2)、求:的面积;(3)、在x轴正半轴上是否存在点P,使是以OA为腰的等腰三角形?若不存在,请说明理由;若存在,请直接写出P的坐标.
(1)、求:点D的坐标;(2)、求:的面积;(3)、在x轴正半轴上是否存在点P,使是以OA为腰的等腰三角形?若不存在,请说明理由;若存在,请直接写出P的坐标.

