2021-2022学年浙教版数学八下第五章特殊平行四边形单元检测卷

试卷更新日期：2022-03-11 类型：单元试卷

进入出卷网下载

一、单选题

1. 下列关于 $\sqrt{2}$ 的说法，错误的是（）

A、 $\sqrt{2}$ 是无理数 B、面积为2的正方形边长为 $\sqrt{2}$ C、 $\sqrt{2}$ 是2的算术平方根 D、 $\sqrt{2}$ 的倒数是﹣ $\sqrt{2}$

查看试题解析
2. 要判断一个四边形是否为矩形，下面是4位同学拟定的方案，其中正确的是（）

A、测量两组对边是否分别相等 B、测量两条对角线是否互相垂直平分 C、测量其中三个内角是作都为直角 D、测量两条对角线是否相等

查看试题解析
3. 在平面直角坐标系中，已知点P（a，a＋8）是第二象限一动点，另点A的坐标为（﹣6，0），则以下结论：①点P在直线y＝x＋8上；②﹣6＜a＜0；③若设△OPA的面积为S，当a＝﹣5时，S＝9；④过P作PE⊥x轴于点E，PF⊥y轴于点F，矩形OEPF的周长始终不变为16，其中正确的有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
4. 如图，已知四边形 $A B C D$ 是矩形，点 $M$ 在 $B C$ 上， $B M = C D$ ，点 $N$ 在 $C D$ 上，且 $D N = C M ， D M$ 与 $B N$ 交于点 $P$ ，则 $D M ： B N =$ （）

A、 $\sqrt{3} ： 2$ B、 $1 ： \sqrt{2}$ C、 $\sqrt{2} ： \sqrt{3}$ D、 $2 ： \sqrt{5}$

查看试题解析
5. 菱形ABCD的边长为13cm，其中对角线BD长10cm，菱形ABCD的面积为（）

A、60cm² B、120cm² C、130cm² D、240cm²

查看试题解析
6. 已知菱形的周长为40 $c m$ ，两条对角线的长度比为3：4，那么两条对角线的长分别为（）

A、6 $c m$ ，8 $c m$ B、3 $c m$ ，4 $c m$ C、12 $c m$ ，16 $c m$ D、24 $c m$ ，32 $c m$

查看试题解析
7. 如图，菱形ABCD的对角线AC、BD相交于点O，AC＝10，BD=4，EF为过点O的一条直线，则图中阴影部分的面积为（）

A、5 B、6 C、8 D、12

查看试题解析
8. 如图，Rt△ABC中，∠BAC＝90°，分别以△ABC的三边为边作正方形ABDE，正方形BCFG，正方形ACHI，AI交CF于点J.三个正方形没有重叠的部分为阴影部分，设四边形BGFJ的面积为S₁ ，四边形CHIJ的面积为S₂ ，若S₁﹣S₂＝12，S_△_ABC＝4，则正方形BCFG的面积为（）

A、16 B、18 C、20 D、22

查看试题解析
9. “赵爽弦图”巧妙地利用面积关系证明了勾股定理，是我国古代数学的骄傲，如图所示的“赵爽弦图”是由四个全等直角三角形和一个小正方形拼成的一个大正方形，设直角三角形较长直角边长为a，较短直角边长为b，若（a+b）²＝21，小正方形的面积为5，则大正方形的面积为（）

A、13 B、14 C、15 D、16

查看试题解析
10. 在直线l上依次摆放着七个正方形，已知斜放置的三个正方形的面积分别是1，2，3，正放置的四个正方形的面积依次是S₁ ， S₂ ， S₃ ， S₄ ，则S₁+S₂+S₃+S₄=（　　）

A、4 B、5 C、6 D、7

查看试题解析

二、填空题

11. 如图，把面积为5的正方形ABCD放到数轴上，使得正方形的一个顶点A与 $- 1$ 重合，那么顶点B在数轴上表示的数是．

查看试题解析
12. 如图，以 $R t △ A B C$ 的两条直角边和斜边为边长分别作正方形，其中正方形 $A B F G$ 、正方形 $A C D E$ 的面积分别为25、144，则阴影部分的面积为.

查看试题解析
13. 如图，在菱形ABCD中对角线AC、BD相交于点O，若AB=3，BD=4，则菱形ABCD的面积为.

查看试题解析

14. 阅读下面材料：

在数学课上，老师提出如下问题：

尺规作图：作对角线等于已知线段的菱形.

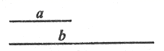已知：两条线段a、b.

求作：菱形AMBN，使得其对角线分别等于b和2a.

小军的作法如下：

如图

(1)画一条线段AB等于b；

(2)分别以A、B为圆心，大于 $\frac{1}{2}$ AB的长为半径，

在线段AB的上下各作两条弧，两弧相交于P、Q两点；

(3)作直线PQ交AB于O点；

(4)以O点为圆心，线段a的长为半径作两条弧，交直线PQ于M、N两点，连接AM、AN、BM、BN.所以四边形AMBN就是所求的菱形.

老师说：“小军的作法正确.”

该上面尺规作图作出菱形AMBN的依据是

查看试题解析

15. 长方形ABCD在平面直角坐标系中的位置如图所示，若AD＝5，点B的坐标为（﹣3，3），则点C的坐标为．

查看试题解析
16. 如图，在平面直角坐标系中， $A$ ， $B$ 两点的坐标分别为 $(- 4 ， 0)$ ， $(0 ， 3)$ ，连接 $A B$ .点 $P$ 在第二象限，若以点 $P$ ， $A$ ， $B$ 为顶点的三角形是等腰直角三角形，则点 $P$ 坐标为.

查看试题解析

三、解答题

17. 如图，在 $▱ A B C D$ 中， $A E ⊥ B C$ 于E，点F在边 $A D$ 上， $B E = D F$ ，求证：四边形 $A E C F$ 是矩形.

查看试题解析
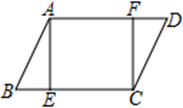18. 如图，在正方形ABCD中，E是CD上一点，F是CB延长线上一点。若DE=BF，求证：∠EAF=90°。

查看试题解析
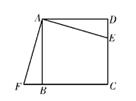19. 如图，在△ABC中，D是BC中点，E是AD，BF的中点，AB＝AC.求证：四边形ADCF是矩形.

查看试题解析
20. 如图，在 $Δ A B C$ 中， $∠ B A C = 90^{\circ}$ ， $A D$ 是中线， $E$ 是 $A D$ 的中点，过点 $A$ 作 $A F ∥ B C$ 交 $B E$ 的延长线于 $F$ ，连接 $C F$ .求证：四边形 $A D C F$ 是菱形.

查看试题解析
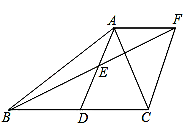21. 如图，在正方形ABCD中，E是对角线AC上一点，FH⊥AC于点E，交AD，AB于点F，H.

(1)、求证：CF＝CH；

(2)、若AH＝ $\frac{1}{3}$ CH，AB＝4，求AH的长.

查看试题解析
22. 已知：如图，在正方形ABCD中，BD为对角线，E、F分别是AD，CD上的点，且AE＝CF，连接BE、BF、EF.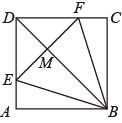

(1)、求证：EM＝FM；

(2)、若DE：AE＝2：1，设S_△ABE＝S，求S_△BEF（用含S的代数式表示）.

查看试题解析
23. 如图，在长方形 $A B C D$ 中， $A B = 4$ ， $B C = 6$ ．延长 $B C$ 到点 $E$ ，使 $C E = 3$ ，连接 $D E$ ．动点 $P$ 从点 $B$ 出发，沿着 $B E$ 以每秒1个单位的速度向终点 $E$ 运动，点 $P$ 运动的时间为 $t$ 秒．

(1)、 $D E$ 的长为；

(2)、连接 $A P$ ，求当 $t$ 为何值时， $△ A B P ≅ △ D C E$ ；

(3)、连接 $D P$ ，求当 $t$ 为何值时， $△ P D E$ 是直角三角形；

(4)、直接写出当 $t$ 为何值时， $△ P D E$ 是等腰三角形．

查看试题解析
24. 如图，在长方形 $A B C D$ 中， $A B = 4$ ， $B C = 9$ ，动点 $Q$ 沿着 $C \to D \to A \to B$ 的方向运动，到点 $B$ 运动停止，设点 $Q$ 运动的路程为 $x$ ， $Δ Q C B$ 的面积为 $y$ .

(1)、点 $Q$ 在 $C D$ 边上，求 $y$ 关于 $x$ 的函数表达式.

(2)、点 $Q$ 在 $A D$ 边上， $Δ Q C B$ 的面积是否发生变化？请说明理由.

(3)、点 $Q$ 在 $A B$ 边上， $Δ Q C B$ 的面积是否发生变化？如果发生变化求出面积的变化范围，并写出 $y$ 关于 $x$ 的函数表达式；如果没有发生变化，求出此时 $Δ Q C B$ 的面积.

查看试题解析

2021-2022学年浙教版数学八下第五章特殊平行四边形 单元检测卷

一、单选题

二、填空题

三、解答题

2021-2022学年浙教版数学八下第五章特殊平行四边形单元检测卷