2021-2022学年浙教版数学八下5.2 菱形 同步练习
试卷更新日期：2022-03-11 类型：同步测试
一、单选题
-
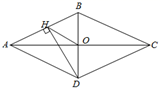
1. 如图，菱形 的对角线 、 相交于点 ，过点 作 于点 ，连接 ，若 ， ，则菱形 的面积为（ ）
A、 B、 C、 D、2. 下列说法中不正确的是（ ）A、平行四边形的对角相等 B、菱形的邻边相等 C、平行四边形的对角线互相平分 D、菱形的对角线互相垂直且相等3. 若菱形的两条对角线的长分别为6和10，则菱形的面积为（ ）A、15 B、24 C、30 D、604. 数学课上，老师让同学们判断一个四边形是否为菱形，下列是某合作小组4位同学拟定的方案，其中正确的是（ ）A、测量对角线是否相等 B、测量对角线是否垂直 C、测量一组对角是否相等 D、测量四边是否相等5. 如图，已知▱ABCD，添加下列一个条件：①AC⊥BD；②∠BAD=90°；③AB=BC；④AC=BD.其中能使▱ABCD成为菱形的是（ ）
A、①③ B、②③ C、③④ D、①②③6. 下面性质中菱形具有而矩形没有的是（ ）A、邻角互补 B、内角和为360° C、对角线相等 D、对角线互相垂直7. 如图， 是菱形 的对角线 ， 的交点， ， 分别是 ， 的中点.下列结论中正确是（ ）① ；②四边形 是菱形；③四边形 的面积为 ，④ .
A、①② B、②④ C、②③ D、③④8. 方方同学在作线段AB的垂直平分线时，他是这样操作的：分别以A和B为圆心，大于 AB的长为半径画弧，两弧相交于点C和点D，则直线CD即为所求，根据他的作图方法可知四边形ADBC一定是（ ）
A、矩形 B、菱形 C、正方形 D、梯形9. 如图，四边形ABCD是菱形，点E、F分别在边BC、CD上，且BE＝DF，AB＝AE，若∠EAF＝75°，则∠C的度数为（ ）
A、85° B、90° C、95° D、105°10. 若菱形 的对角线 、 的长分别为6和8，则这个菱形的周长是（ ）A、20 B、24 C、40 D、48二、填空题
-
11. 已知菱形ABCD的边长为6，∠ABC=60°，则对角线AC的长是.12. 在矩形ABCD中，AD=5，AB=4，点E，F在直线AD上，且四边形BCFE为菱形，若线段EF的中点为M，则线段AM的长为.13. 在菱形 中， ， ，则菱形 的周长是.
14. 如图，在菱形ABCD中，对角线AC、BD相交于点O，AC＝16，BD＝12，E是边AD上一点，直线OE交BC于点F，将菱形沿直线EF折叠，使点B的对应点为B'，点A的对应点为A′，若AE＝4，则 的长等于.
15. 菱形ABCD中，∠B＝60°，AB＝5，以AC为边长作正方形ACFE，则点D到EF的距离为.16. 如图，菱形 的边长为 ， ，点 是 边上任意一点（可以与点 或点 重合）， 分别过点 、 、 作射线 的垂线，垂足分别是 、 、 ，设 ，则 的取值范围是.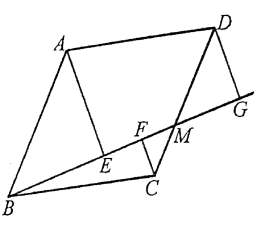
三、解答题
-
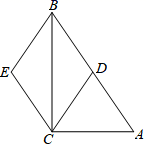
17. 如图，在 中， ， 为 边上的中线，过点 作 ，过点 作 ， 与 相交于点 .求证：四边形 为菱形.
18. 如图，四边形ABCD是菱形，对角线AC，BD相交于点O，DH⊥AB 于点H，连OH接，求证：∠DHO=∠DCO.
19. 在矩形ABCD中，AB=3，AD=9，对角线AC、BD交于点O，一直线过O点分别交AD、BC于点E、F，且ED=4，求证：四边形AFCE为菱形。
20. 已知：菱形ABCD的两条对角线AC与BD相交于点O，且AC=6，BD=8，求菱形的周长和面积.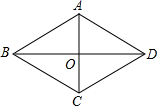
21. 如图，菱形ABCD的对角线AC，BD相交于点O，过点D作DE//AC且DE=OC，连结CE.
(1)、求证：四边形OCED是矩形.(2)、连结AE交OD于点F，若菱形ABCD的边长为6，∠ABC=60°，求AE的长.22. 如图，在矩形ABCD中，O为对角线AC的中点，过点O作直线分别与矩形的边AD，BC交于M，N两点，连接CM，AN．
(1)、求证：四边形ANCM为平行四边形；(2)、若AD＝4，AB＝2，且MN⊥AC，求DM的长．
