2021-2022学年浙教版数学八下5.1 矩形同步练习

试卷更新日期：2022-03-11 类型：同步测试

进入出卷网下载

一、单选题

1. 下列四个命题中，正确的是（）

A、对角线相等的四边形是矩形 B、有一个角是直角的四边形是矩形 C、两组对边分别相等的四边形是矩形 D、四个角都相等的四边形是矩形

查看试题解析
2. 如图，有两棵树，一棵高19米，另一棵高10米，两树相距12米.若一只小鸟从一棵树的树梢飞到另一棵树的树梢，则小鸟至少飞行（）

A、10米 B、15米 C、16米 D、20米

查看试题解析
3. 如图所示，点O是矩形ABCD的对角线AC的中点，OE//AB交AD于点E.若OE=3，BC=8，则OB的长为（）

A、4 B、5 C、 $\frac{\sqrt{34}}{2}$ D、 $\sqrt{34}$

查看试题解析
4. 如图，矩形 $A B O C$ 的顶点坐标为 $(- 4 ， 5)$ ， D是 $O B$ 的中点，E为 $O C$ 上的一点，当 $Δ A D E$ 的周长最小时，点E的坐标是（）

A、 $(0 ， \frac{4}{3})$ B、 $(0 ， \frac{5}{3})$ C、 $(0 ， 2)$ D、 $(0 ， \frac{10}{3})$

查看试题解析
5. 如图，在矩形纸片ABCD中，AB＝6，BC＝8，点M为AB上一点，将△BCM沿CM翻折至△ECM，ME与AD相交于点G，CE与AD相交于点F，且AG＝GE，则BM的长度是（）

A、 $\frac{18}{5}$ B、4 C、 $\frac{24}{5}$ D、5

查看试题解析
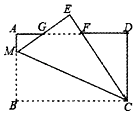6. 如图，已知长方形 $A B C D$ 中， $A D = 8 c m$ ， $A B = 6 c m$ ，点E为AD的中点，若点P在线段AB上以 $2 c m / s$ 的速度由点A向点B运动.同时，点Q在线段BC上由点C向点B运动，若 $△ A E P$ 与 $△ B P Q$ 全等，则点Q的运动速度是（）

A、6或 $\frac{8}{3}$ B、2或6 C、2或 $\frac{2}{3}$ D、2或 $\frac{8}{3}$

查看试题解析
7. 一长方形操场，其中一边长为 $2 a + b$ ，另一边长为 $a$ ，则该操场的面积为（）

A、 $3 a + b$ B、 $6 a + 2 b$ C、 $2 a^{2} + a b$ D、 $2 a^{2} b$

查看试题解析
8. 在Rt△ABC中，∠C＝90°，AB＝5，AC＝3，点P为边AB上一动点（且点P不与点A，B重合），PE⊥BC于E，PF⊥AC于F，点M为EF中点，则PM的最小值为（）

A、 $\frac{6}{5}$ B、 $\frac{12}{5}$ C、 $\frac{4}{3}$ D、 $\frac{5}{4}$

查看试题解析
9. 图1是长为 $a$ ，宽为 $b (a > b)$ 的小长方形纸片将6张如图1的纸片按图2的方式不重叠地放在长方形 $A B C D$ 内，已知 $C D$ 的长度固定不变， $B C$ 的长度可以变化，图中阴影部分（即两个长方形）的面积分别表示为 $S_{1}$ ， $S_{2}$ ，若 $S = S_{1} - S_{2}$ ，且 $S$ 为定值，则 $a$ ， $b$ 满足的关系是 $($ $)$

A、 $a = 2 b$ B、 $a = 3 b$ C、 $a = 4 b$ D、 $a = 5 b$

查看试题解析
10. 如图，△ABC中，BC＝4，D、E 分别是线段AB和线段BC上的动点，且BD=DE，F是线段AC上一点，且EF=FC，则DF的最小值为（　　）

A、3 B、2 C、2.5 D、4

查看试题解析

二、填空题

11. 如图，在矩形ABCD中，对角线AC，BD交于点O，若∠COD=52°，则∠CAD=.

查看试题解析
12. 如图所示，在矩形ABCD中，AB=2，BC=3，对角线AC的垂直平分线分别交AD，BC于点E，F，连结CE，则CE的长为.

查看试题解析
13. 如图，在四边形ABCD中，点E，F，G，H分别为边AD，AB，C BC，CD的中点。

(1)、四边形EFGH的形状是；

(2)、若对角线AC⊥BD，垂足为点O，AC=8，BD=6，则四边形EFGH的周长为。

查看试题解析
14. 由10块相同的小长方形地砖拼成一个面积为3.6m²的长方形ABCD（如图），则长方形ABCD的周长为.

查看试题解析
15. 如图，在矩形 $O A B C$ 中， $O A = 2$ ， $O C = 1$ ， $O B = O D$ ，数轴上点 $D$ 所表示的数是．

查看试题解析
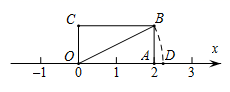16. 如图，矩形ABCD中，AB＝9，AD＝12，点M在对角线BD上，点N为射线BC上一动点，连接MN，DN，且∠DNM＝∠DBC，当 $△$ DMN是等腰三角形时，线段BN的长为．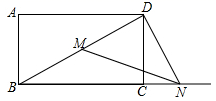

查看试题解析

三、解答题

17. 如图，已知长方形ABCD中，如图，在长方形ABCD中，AD＝BC＝8，BD＝10，点E从点D出发，以每秒2个单位长度的速度沿DA向点A匀速移动，点F从点C出发，以每秒1个单位长度的速度沿CB向点B匀速移动，点G从点B出发，沿BD向点D匀速移动，三个点同时出发，当E点到达终点时，其余两点也随之停止运动，假设移动时间为t秒，当△DEG和△BFG全等时，求t的值和此时G点对应的速度.

查看试题解析
18. 如图，将平行四边形ABCD的边DC延长到点E ，使CE＝DC ，连结AE ，交BC于点F ， ∠AFC＝2∠D ，连结AC、BE ．求证：四边形ABEC是矩形．

查看试题解析
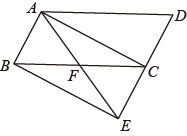19. 如图，在▱ABCD中，过点D作DE⊥AB于点E，点F在边CD上，DF＝BE.求证：四边形BEDF是矩形．

查看试题解析
20. 已知：如图，在△ABC中，AB＝AC，D为BC中点，四边形ABDE是平行四边形．
求证：四边形ADCE是矩形．

查看试题解析
21. 为了节省材料，某水产养殖户利用水库的岸堤（岸堤足够长）为一边，用总长为80m的围网在水库中围成了如图所示的①，②，③三块长方形区域，且这三块长方形区域的面积相等.设BC的长度为xm.

(1)、用含x的代数式表示BE=m，AE=m；

(2)、x为多少时，长方形ABCD区域的面积为225m²？

查看试题解析
22. 如图所示，某公司计划用32m长的材料沿墙建造长方形仓库，仓库的一边靠墙，已知墙长16m，设长方形的宽AB为x m.

(1)、用含x的代数式表示长方形的长BC；

(2)、能否建造成面积为120m²的长方形仓库？若能，求出长方形仓库的长和宽；若不能，请说明理由.

(3)、能否建造成面积为160m²的长方形仓库？若能，求出长方形仓库的长和宽；若不能，请说明理由.

查看试题解析
23. 阅读理解：课外兴趣小组活动时，老师提出了如下问题：
如图1，△ABC中，若AB=8，AC=6，求BC边上的中线AD的取值范围.小明在组内经过合作交流，得到了如下的解决方法：延长AD到点E，使DE=AD，请根据小明的方法思考：

(1)、由已知和作图能得到△ADC≌△EDB的理由是____。

A、SSS B、SAS C、AAS D、HL

(2)、求得AD的取值范围是____。

A、6<8 B、6 $\leq$ AD $\leq$ 8 C、1<7 D、1≤AD≤7

(3)、解题时，条件中若出现中点"中点"“中线”字样，可以考虑延长中线构造全等三角形，把分散的已知条件和所求证的结论集合到同一个三角形中。
问题解决：如图2，AD是△ABC的中线，BE交AC于E，交AD于F，且AE=EF，求证：AC=BF。

查看试题解析
24. 如图，在△ABC和△DEB中，AC∥BE，∠C＝90°，AB＝DE，点D为BC的中点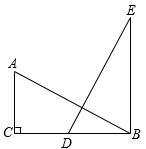， $A C = \frac{1}{2} B C$ ．

(1)、求证：△ABC≌△DEB．

(2)、连结AE，若BC＝4，直接写出AE的长．

查看试题解析

2021-2022学年浙教版数学八下5.1 矩形 同步练习

一、单选题

二、填空题

三、解答题

2021-2022学年浙教版数学八下5.1 矩形同步练习