2021-2022学年浙教版数学八下第四章 平行四边形 单元检测卷
试卷更新日期：2022-03-11 类型：单元试卷
一、单选题
-
1. 电动伸缩门是依据平行四边形的（ ）A、可变形 B、伸缩性 C、稳定性 D、不稳定性2. 已知在▱ABCD中，∠B+∠D=200°，则∠B的度数为（ ）A、100° B、160° C、80° D、60°3. 如图下面图形既是轴对称图形，又是中心对称图形的是（ ）A、
B、
C、
D、
4. 用反证法证明命题：“已知△ABC，AB＝AC，求证：∠B＜90°.”第一步应先假设（ ）A、∠B≥90° B、∠B＞90° C、∠B＜90° D、AB≠AC5. 如果一个多边形的每一个外角都是36°，则这个多边形的边数是（ ）A、8 B、10 C、12 D、146. 如图，在平行四边形ABCD中，过对角线BD上一点P，作EF∥BC，HG∥AB，若四边形AEPH和四边形CFPG的面积分另为S1和S2 ， 则S1与S2的大小关系为（ ）
A、S1=S2 B、S1＞S2 C、S1＜S2 D、不能确定7. 下列∠A：∠B：∠C：∠D的值中，能判定四边形ABCD是平行四边形的是（ ）A、1：2：3：4 B、1：4：2：3 C、1：2：2：1 D、3：2：3：28. 如图，在 中，点E，F在对角线 上，连接 ，点E，F满足以下条件中的一个：① ；② ；③ ；④ ；⑤ .
其中，能使四边形 为平行四边形的条件个数为（ ）
A、2 B、3 C、4 D、59. 在四边形 中，对角线 、 相交于点 ，在下列条件中，① ， ，② ， ；③ ， ，④ ， ，⑤ ， 能够判定四边形 是平行四边形的个数有（ ）
A、2个 B、3个 C、4个 D、5个10. 用反证法证明“三角形中至少有一个内角大于或等于60°”时，应假设（ ）A、三角形的两个内角小于60° B、三角形的三个内角都小于60° C、三角形的两个内角大于60° D、三角形的三个内角都大于60°二、填空题
-
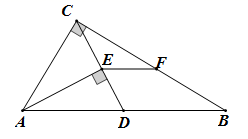
11. 用反证法证明：“在△ABC中，若AB≠AC ， 则∠B≠∠C”，则应假设 ．12. 如图，在△ABC中，∠ACB＝90°，AB＝10 cm，BC＝8cm，点D在边AB上，AD＝AC，AE⊥CD，垂足为E，点F是BC的中点，则EF＝cm.
13. 如图，在 □ ABCD中，EF∥AD，HN∥AB，则图中的平行四边形共有个。
14. 如图， 和 关于点C成中心对称，若 ， ， ，则 的长是.
15. 如图所示，在平面直角坐标系中，四边形OABC是平行四边形，AB=2，OA= ， ∠AOC=45°，则点B的坐标是。
16. 如图，△ABC中，点D，E分别在AB，BC边上.比较大小，∠A＋∠C∠1＋∠2.
三、解答题
-
17. 用反证法证明：一个三角形中不能有两个直角。18. 如图，在四边形ABCD中，点E，F分别是边AB，AD的中点，若BC=15，CD=9，EF=6，∠AFE=55°，求∠ADC的度数。
19. 如图所示，在梯形ABCD中，DC∥AB，点E是BC的中点，连结AE并延长与DC的延长线相交于点F，连结BF，AC。求证：四边形ABFC是平行四边形。
20. 四边形ABCD中，AB∥CD，AD∥BC，O为对角线AC的中点，过O点作直线EF，交DA的延长线于点E，交BC的延长线于点F。求证：四边形AECF是平行四边形.
21. 如图，在ABC中，AC边的垂直平分线DM交AC于D，CB边的垂直平分线EN交BC于E，DM与EN相交于点F.
(1)、若CMN的周长为16cm，求AB的长；(2)、若∠MFN=70°，求∠MCN的度数.22. 如图，四边形ABCD为平行四边形，E为AD上的一点，连结EB并延长至点F，使BF=BE，连结EC并延长至点G，使CG=CE，连结FG.H为FG的中点，连结DH，AF。
(1)、求证：四边形AFHD为平行四边形；(2)、若CB=CE，∠EBC=75°，∠DCE=10°，求∠DAB的度数。
