2021-2022学年浙教版数学八下4.5 三角形的中位线同步练习
试卷更新日期：2022-03-11 类型：同步测试
一、单选题
-
1. 如图，在△ABC中，延长BC至点D，使得CD= BC，过AC的中点E作EF∥CD(点F位于点E右侧)，且EF=2CD，连结DF.若AB=8，则DF的长为（ ）
A、3 B、4 C、2 D、32. 如图，在四边形ABCD中，AD=BC，E，F，G分别是AB，CD，AC的中点，若∠DAC=20°，∠ACB=84°，则∠FEG等于（ ）
A、32° B、38° C、64° D、30°3. 如图所示，在△ABC中，D，E分别是BC，AC的中点，BF平分∠ABC，交DE于点F，若BC=6，则DF的长是（ ）
A、2 B、3 C、5 D、44. 如图，为测量池塘岸边A，B两点之间的距离，小亮在池塘的一侧选取一点O，测得OA，OB的中点D，E之间的距离是14米，则A，B两点之间的距离是（ ）
A、18米 B、24米 C、28米 D、30米5. 如图，在▱ABCD中，对角线AC，BD交于点O，点E是BC的中点。若OE=3cm，则AB的长为（ ）
A、3cm B、6cm C、9cm D、12cm6. 如图，在△ABC中，点D，E分别是AB，AC的中点，∠A=50°，∠ADE=60°，则∠C的度数为（ ）
A、70° B、60° C、50° D、40°7. 如图，在四边形ABCD中，∠A=90°，AB=3 ， AD=3，点M，N分别为线段BC，AB上的动点（含端点，但点M不与点B重合），点E，F分别为DM，MN的中点，则EF长度的最大值为（ ）
A、3 B、4 C、4.5 D、58. 如图，在△ABC中，点D、E、F分别是各边的中点，若△ABC的面积为16cm2 ， 则△DEF的面积是（ ）cm2.
A、2 B、4 C、6 D、89. 如图，平行四边形ABCD的对角线AC、BD相交于点O，AE平分∠BAD，分别交BC、BD于点E、P，连接OE，∠ADC=60°， ， 则下列结论：①∠CAD=30° ② ③S平行四边形ABCD=AB•AC ④ ，正确的个数是（ ）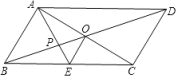
A、1 B、2 C、3 D、410. 如图，四边形ABCD中，∠ABC=120°，点F为CD中点，以AB，BD为边，AD为对角线作平行四边形ABDE，连接BE交AD于点O，且OF=BC=2，则AB的长为（ ）
A、 B、 C、 D、二、填空题
-
11. 如图，平行四边形ABCD，对角线AC、BD相交于点O，点E是CD的中点， ，则AD的长是.
12. 如图所示，点D，E，F分别是△ABC各边的中点，BH⊥AC，垂足为H，DE=8cm，则FH的长为cm.
13. 如图，在Rt△ABC中，∠B=90°，AB=2 ， BC=3，D，E分别是AB，AC的中点，延长BC至点F，使CF=BC，连结DF，EF，则EF的长为。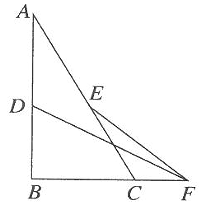
14. 如图，平行四边形ABCD的对角线AC，BD相交于点O，点E，F分别是线段AO，BO的中点。若AC+BD=24cm，△OAB的周长是20cm，则EF=cm。
15. 如图，在四边形ABCD中，P是对角线BD的中点，E，F分别是AB，CD的中点，AD=BC，∠PEF=18°，则∠PFE的度数是。
16. 如图，DE是△ABC的中位线，AF是BC边上的中线，DE，AF交于点O.现有以下结论：①DE∥BC；②OD=BC；③AO=FO；④S△AOD=S△ABC ， 其中正确结论的序号为。
三、解答题
-
17. 如图所示，在Rt△ABC中，∠ACB=90°，点D，E分别是边AB，AC的中点，延长BC至点F，使CF=BC，若AB=10，求EF的长。
18. 如图，△ABC是锐角三角形，分别以AB，AC为边向外侧作等腰△ABM和等腰△CAN，AM=AB AC=AN，∠MAB=∠CAN.D，E，F分别是MB，BC，CN的中点，连结DE，EF.求证：DE=EF。
19. 如图所示，已知E为▱ABCD中DC边的延长线上的一点，且CE=DC，连结AE，分别交BC，BD于点F，G，连结AC交BD于点O，连结OF。求证：AB=2OF。
20. 如图，在△ABC中，点D，E分别是边BC，AC的中点，连结DE，AD，点F在BA的延长线上，且AF=AB，连结EF，判断四边形ADEF的形状，并加以证明。
21. 如图所示，在△ABC中，D是边BC的中点，点E在△ABC内，AE平分∠BAC，CE⊥AE，点F在边AB上，EF//BC.
(1)、求证：四边形BDEF是平行四边形.(2)、线段BF，AB，AC的数量之间具有怎样的关系？证明你所得到的结论.22. 如图，已知在△ABC中，D，E，F分别是AB， BC，AC的中点，连结DF，EF，BF。
(1)、求证：四边形BEFD是平行四边形；(2)、若∠AFB=90°，AB=6，求四边形BEFD的周长。23. 如图，在▱ABCD中，点E，F分别从点A，B同时出发，沿AD，BC方向以相同的速度运动（分别运动到点D，C即停止），AF与BE相交于点G，CE与DF相交于点H。
(1)、若AD=8cm，则在此运动过程中，线段GH的长始终等于cm；(2)、当E，F分别运动到AD，BC的中点时，求证：EF与GH互相平分。24. 如图，在△ABC中，∠C＝90°，AB＝5cm，BC＝3cm，若动点P从点C开始，按C→A→B的路径运动，且速度为每秒2cm，设点P的运动时间为t秒.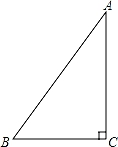
(1)、则AC＝cm；
(2)、当BP平分∠ABC，求此时点P的运动时间t的值；(3)、点P运动过程中，△BCP能否成为等腰三角形？若能，求出t的值；若不能请说明理由.