2021-2022学年浙教版数学八下4.4 平行四边形的判定同步练习
试卷更新日期：2022-03-10 类型：同步测试
一、单选题
-
1. 在四边形ABCD中，O是对角线交点，下列条件中，不能判定四边形ABCD是平行四边形的是（ ）A、AD∥BC，AD=BC B、AB=DC，AD=BC C、AB∥DC，AD=BC D、OA=OC，OD=OB2. 如图，在四边形ABCD中，AB∥CD，要使四边形ABCD是平行四边形，下列可添加的条件不正确的是（ ）
A、AD=BC B、AB=CD C、AD∥BC D、∠A=∠C3. 点A，B，C，D在同一平面内，有以下条件：①AB∥DC；②AB=DC；③BC∥AD；④BC=AD。从四个条件中任意选取两个，能使四边形ABCD是平行四边形的选法有 （ ）A、3种 B、4种 C、5种 D、6种4. 下列条件中，不能判定四边形是平行四边形的条件是（ ）A、两组对边分别平行 B、两组对边分别相等 C、一组对边平行，另一组对边相等 D、一组对边平行且相等5. 平行四边形ABCD中，E，F是对角线BD上不同的两点，下列条件中，不能得出四边形AECF一定为平行四边形的是（ ）A、BE=DF B、AE=CF C、AF//CE D、∠BAE=∠DCF6. 如图所示，四边形ABCD是平行四边形，按下列条件得到的四边形BFDE是平行四边形的有（ ）
①图甲，DE⊥AC，BF⊥AC；②图乙，DE平分∠ADC，BF平分∠ABC；③图丙，E是AB的中点，F是CD的中点；④图丁，E是AB上一点，EF⊥AB。
A、3个 B、4个 C、1个 D、2个7. 如图，在▱ABCD中，对角线AC，BD相交于点O，将△AOB平移至△DPC的位置，连结OP，则图中平行四边形的个数为（ ）
A、1 B、2 C、3 D、48. 小玲的爸爸在钉制平行四边形框架时，采用了一种方法：如图所示，将两根木条AC，BD的中点重叠，并用钉子固定，则四边形ABCD就是平行四边形，这种方法的依据是（ ）
A、对角线互相平分的四边形是平行四边形 B、两组对角分别相等的四边形是平行四边形 C、两组对边分别相等的四边形是平行四边形 D、两组对边分别平行的四边形是平行四边形9. 如图所示，直线a∥b，另有一条直线l与直线a，b分别交于点A，B，若将直线l作平移运动，则线段AB的长度（ ）
A、变大 B、变小 C、不变 D、变大或变小要看直线l平移的方向10. 下列说法中，错误是（ ）A、对角线互相平分的四边形是平行四边形 B、两组对角分别相等的四边形是平行四边形 C、一组对边平行且相等的四边形是平行四边形 D、一组对边平行另一组对边相等的四边形是平行四边形二、填空题
-
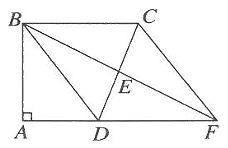
11. 在四边形ABCD中，AC，BD相交于点O，且OA=OC，OB=OD，∠ABC=70°，则∠BCD=。12. 如图，AD为△ABC的中线，AB=9，AC=12，延长AD至点E，使DE=AD，连结BE，CE，则四边ABEC的周长是。
13. 如图所示，AO=OC，BD=16cm，则当OB=cm时，四边形ABCD是平行四边形。
14. 如图所示，在▱ABCD中，对角线交于点O，点E，F在对角线AC上（不同于点A，C），当点E，F的位置满足的条件时，四边形DEBF是平行四边形。
15. 在四边形ABCD中，对角线AC与BD交于点O已知OA=OC，添加①AB=DC，②AB∥DC③OB=OD中的一个不能判定这个四边形是平行四边形的是。（填序号）16. 如图，点D是直线l外一点，在l上取两点A，B，连结AD，分别以点B，D为圆心，AD，AB的长为半径画弧，两弧交于点C，连结CD，BC，则四边形ABCD是平行四边形，理由是：。
三、解答题
-
17. 如图，在▱ABCD中，E，F是对角线BD上的两点（点E在点F左侧），且∠AEB=∠CFD=90°。
求证：四边形AECF是平行四边形。
18. 如图，AB，CD相交于点O，AC∥DB，AO=BO，E，F分别是OC，OD的中点。求证：四边形AFBE是平行四边形。
19. 如图，四边形ABCD是平行四边形，E，F是对角线BD上的两点，且BF=ED。求证：∠EAF=∠FCE.
20. 如图所示，在四边形ABCD中，M是边BC的中点，AM，BD互相平分并交于点O。求证：四边形AMCD是平行四边形。
21. 如图，在平行四边形ABCD中，点E，F分别是边AD，BC的中点．
(1)、求证：AF＝CE；(2)、若四边形AECF的周长为10，AF＝3，AB＝2，求平行四边形ABCD的周长．22. 已知：如图，在ABCD中，对角线AC，BD相交于点O，点E，F在AC上，点G，H在BD上，且AE=CF，BG= DH。
(1)、若AC=6，BD=8，试求AD的取值范围；(2)、若AC=AD，∠CAD=50°，试求∠ABC的度数；(3)、求证：四边形EHFG是平行四边形。
